第97页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
8. 如图,AB是$\odot O$的直径,BC交$\odot O$于点D,$DE⊥AC$于点E.若要使直线DE是$\odot O$的切线,还需补充一个条件,则下列补充的条件不正确的是 (
A.$DE= DO$
B.$AB= AC$
C.$CD= DB$
D.$AC// OD$
A
)A.$DE= DO$
B.$AB= AC$
C.$CD= DB$
D.$AC// OD$
答案:
解:连接OD。
对于选项B:若AB=AC,则∠B=∠C。
∵OB=OD,
∴∠B=∠ODB,
∴∠ODB=∠C,
∴OD//AC。
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线。
对于选项C:若CD=DB,OA=OB,
∴OD是△ABC的中位线,
∴OD//AC。
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线。
对于选项D:若AC//OD,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线。
对于选项A:DE=DO,无法得出DE⊥OD,不能判定DE是⊙O的切线。
答案:A
对于选项B:若AB=AC,则∠B=∠C。
∵OB=OD,
∴∠B=∠ODB,
∴∠ODB=∠C,
∴OD//AC。
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线。
对于选项C:若CD=DB,OA=OB,
∴OD是△ABC的中位线,
∴OD//AC。
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线。
对于选项D:若AC//OD,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线。
对于选项A:DE=DO,无法得出DE⊥OD,不能判定DE是⊙O的切线。
答案:A
9. 如图,菱形OABC的顶点A,B,C在$\odot O$上,过点B作$\odot O$的切线,交OA的延长线于点D.若$\odot O$的半径为1,则BD的长为 (
A.1
B.2
C.$\sqrt {2}$
D.$\sqrt {3}$
D
)A.1
B.2
C.$\sqrt {2}$
D.$\sqrt {3}$
答案:
【解析】:本题可根据菱形的性质、圆的性质以及切线的性质,通过证明三角形全等,进而求出$BD$的长。
步骤一:连接$OB$,分析相关性质
因为四边形$OABC$是菱形,所以$OA = AB$。
又因为$OA = OB$(圆的半径),所以$OA = AB = OB$,那么$\triangle OAB$是等边三角形。
根据等边三角形的性质可知,$\angle AOB = 60^{\circ}$。
步骤二:利用切线性质得到直角
因为$BD$是$\odot O$的切线,$OB$是半径,根据圆的切线性质:圆的切线垂直于经过切点的半径,所以$OB\perp BD$,即$\angle OBD = 90^{\circ}$。
步骤三:求出$\angle D$的度数
在$\triangle OBD$中,已知$\angle OBD = 90^{\circ}$,$\angle AOB = 60^{\circ}$,$OA = OB$,且$OD$为公共边,所以$\triangle OBD$是直角三角形,$\angle D = 30^{\circ}$。
步骤四:根据直角三角形性质求出$BD$的长
在直角三角形中,$30^{\circ}$所对的直角边等于斜边的一半。
在$Rt\triangle OBD$中,$\angle D = 30^{\circ}$,$OB$是$30^{\circ}$角所对的直角边,$OD$是斜边,且$OB = 1$(圆的半径为$1$)。
根据勾股定理$BD=\sqrt{OD^{2}-OB^{2}}$,因为$OD = 2OB = 2$,所以$BD = \sqrt{2^{2} - 1^{2}}=\sqrt{3}$。
【答案】:D
步骤一:连接$OB$,分析相关性质
因为四边形$OABC$是菱形,所以$OA = AB$。
又因为$OA = OB$(圆的半径),所以$OA = AB = OB$,那么$\triangle OAB$是等边三角形。
根据等边三角形的性质可知,$\angle AOB = 60^{\circ}$。
步骤二:利用切线性质得到直角
因为$BD$是$\odot O$的切线,$OB$是半径,根据圆的切线性质:圆的切线垂直于经过切点的半径,所以$OB\perp BD$,即$\angle OBD = 90^{\circ}$。
步骤三:求出$\angle D$的度数
在$\triangle OBD$中,已知$\angle OBD = 90^{\circ}$,$\angle AOB = 60^{\circ}$,$OA = OB$,且$OD$为公共边,所以$\triangle OBD$是直角三角形,$\angle D = 30^{\circ}$。
步骤四:根据直角三角形性质求出$BD$的长
在直角三角形中,$30^{\circ}$所对的直角边等于斜边的一半。
在$Rt\triangle OBD$中,$\angle D = 30^{\circ}$,$OB$是$30^{\circ}$角所对的直角边,$OD$是斜边,且$OB = 1$(圆的半径为$1$)。
根据勾股定理$BD=\sqrt{OD^{2}-OB^{2}}$,因为$OD = 2OB = 2$,所以$BD = \sqrt{2^{2} - 1^{2}}=\sqrt{3}$。
【答案】:D
10. 如图,$∠ACB= 60^{\circ }$,BC与直径为4cm的$\odot O$相切于点C.若将$\odot O$沿CB向右滚动,则当滚动到$\odot O$与CA也相切时,圆心O移动的水平距离是
$2\sqrt{3}$
cm.
答案:
1. 首先,设滚动到$\odot O'$与$CA$、$CB$分别相切于点$D$、$C$:
因为$CA$、$CB$是$\odot O'$的切线,根据切线长定理,$O'C$平分$\angle ACB$。
已知$\angle ACB = 60^{\circ}$,所以$\angle O'CB=\frac{1}{2}\angle ACB = 30^{\circ}$。
已知圆的直径$d = 4cm$,则半径$r = 2cm$。
2. 然后,在$Rt\triangle O'CE$($E$为圆心$O$移动到$O'$时,过$O'$作$O'E\perp CB$,$E$在$CB$上):
因为$\odot O$与$CB$相切,滚动后$\odot O'$与$CB$也相切,圆心移动的轨迹与$CB$平行。
在$Rt\triangle O'CE$中,$\angle O'CE = 30^{\circ}$,$\angle O'EC = 90^{\circ}$,$O'C=r = 2cm$。
根据三角函数关系$\cos\angle O'CE=\frac{CE}{O'C}$。
由$\cos30^{\circ}=\frac{\sqrt{3}}{2}$,且$O'C = 2cm$,根据$CE = O'C\cdot\cos\angle O'CE$。
把$O'C = 2cm$,$\angle O'CE = 30^{\circ}$代入可得:$CE=O'C\cdot\cos30^{\circ}$。
因为$O'C = 2cm$,所以$CE = 2×\frac{\sqrt{3}}{2}=\sqrt{3}cm$。
所以圆心$O$移动的水平距离是$2\sqrt{3}cm$。
因为$CA$、$CB$是$\odot O'$的切线,根据切线长定理,$O'C$平分$\angle ACB$。
已知$\angle ACB = 60^{\circ}$,所以$\angle O'CB=\frac{1}{2}\angle ACB = 30^{\circ}$。
已知圆的直径$d = 4cm$,则半径$r = 2cm$。
2. 然后,在$Rt\triangle O'CE$($E$为圆心$O$移动到$O'$时,过$O'$作$O'E\perp CB$,$E$在$CB$上):
因为$\odot O$与$CB$相切,滚动后$\odot O'$与$CB$也相切,圆心移动的轨迹与$CB$平行。
在$Rt\triangle O'CE$中,$\angle O'CE = 30^{\circ}$,$\angle O'EC = 90^{\circ}$,$O'C=r = 2cm$。
根据三角函数关系$\cos\angle O'CE=\frac{CE}{O'C}$。
由$\cos30^{\circ}=\frac{\sqrt{3}}{2}$,且$O'C = 2cm$,根据$CE = O'C\cdot\cos\angle O'CE$。
把$O'C = 2cm$,$\angle O'CE = 30^{\circ}$代入可得:$CE=O'C\cdot\cos30^{\circ}$。
因为$O'C = 2cm$,所以$CE = 2×\frac{\sqrt{3}}{2}=\sqrt{3}cm$。
所以圆心$O$移动的水平距离是$2\sqrt{3}cm$。
11. (2023·启东期中)如图,在$△ABC$中,$AB= AC$,以AB为直径的$\odot O$交AC于点D,连接BD,过点C作$CE// AB$.
(1)请用无刻度的直尺和圆规作图:过点B作$\odot O$的切线,交CE于点F(不写作法,保留作图痕迹,标明字母);
(2)在(1)的条件下,求证:$BD= BF$.
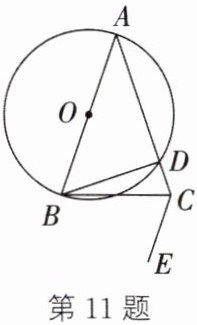
(1)请用无刻度的直尺和圆规作图:过点B作$\odot O$的切线,交CE于点F(不写作法,保留作图痕迹,标明字母);
(2)在(1)的条件下,求证:$BD= BF$.

答案:
1. (1)**作图**:

2. (2)**证明**:
因为$AB = AC$,所以$\angle ABC=\angle ACB$。
因为$AB$是$\odot O$的直径,所以$\angle ADB = 90^{\circ}$,即$BD\perp AC$。
因为$BF$是$\odot O$的切线,所以$\angle ABF = 90^{\circ}$。
又因为$CE// AB$,所以$\angle FCB=\angle ABC$(两直线平行,内错角相等)。
而$\angle ABC=\angle ACB$,所以$\angle FCB=\angle ACB$。
在$\triangle BCD$和$\triangle BCF$中:
$\left\{\begin{array}{l}\angle BDC=\angle BFC = 90^{\circ}\\\angle BCD=\angle BCF\\BC = BC\end{array}\right.$($AAS$判定定理:两角及其中一角的对边对应相等的两个三角形全等)。
根据$AAS$(两角及其中一角的对边对应相等),可得$\triangle BCD\cong\triangle BCF$。
由全等三角形的对应边相等,所以$BD = BF$。
综上,(1)完成作图;(2)证明了$BD = BF$。
1. (1)**作图**:
2. (2)**证明**:
因为$AB = AC$,所以$\angle ABC=\angle ACB$。
因为$AB$是$\odot O$的直径,所以$\angle ADB = 90^{\circ}$,即$BD\perp AC$。
因为$BF$是$\odot O$的切线,所以$\angle ABF = 90^{\circ}$。
又因为$CE// AB$,所以$\angle FCB=\angle ABC$(两直线平行,内错角相等)。
而$\angle ABC=\angle ACB$,所以$\angle FCB=\angle ACB$。
在$\triangle BCD$和$\triangle BCF$中:
$\left\{\begin{array}{l}\angle BDC=\angle BFC = 90^{\circ}\\\angle BCD=\angle BCF\\BC = BC\end{array}\right.$($AAS$判定定理:两角及其中一角的对边对应相等的两个三角形全等)。
根据$AAS$(两角及其中一角的对边对应相等),可得$\triangle BCD\cong\triangle BCF$。
由全等三角形的对应边相等,所以$BD = BF$。
综上,(1)完成作图;(2)证明了$BD = BF$。
12. (2023·内江)如图,正六边形ABCDEF内接于$\odot O$,点P在$\widehat {AF}$上,Q是$\widehat {DE}$的中点,则$∠CPQ$的度数为 (
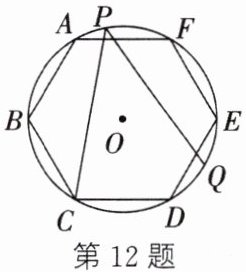
A.$30^{\circ }$
B.$36^{\circ }$
C.$45^{\circ }$
D.$60^{\circ }$
C
)
A.$30^{\circ }$
B.$36^{\circ }$
C.$45^{\circ }$
D.$60^{\circ }$
答案:
解:连接CQ,DQ。
正六边形ABCDEF内接于$\odot O$,则$\odot O$的圆心角为$360^{\circ}$,每条边所对的圆心角为$360^{\circ}÷6 = 60^{\circ}$,即$\angle COD = 60^{\circ}$。
Q是$\widehat{DE}$的中点,$\widehat{DE}$所对圆心角为$60^{\circ}$,故$\widehat{DQ}=\frac{1}{2}\widehat{DE}$,所对圆心角为$30^{\circ}$,即$\angle DOQ = 30^{\circ}$。
$\angle COQ=\angle COD+\angle DOQ=60^{\circ}+30^{\circ}=90^{\circ}$。
$\angle CPQ$是$\widehat{CQ}$所对的圆周角,$\angle COQ$是$\widehat{CQ}$所对的圆心角,所以$\angle CPQ=\frac{1}{2}\angle COQ=\frac{1}{2}×90^{\circ}=45^{\circ}$。
答案:C
正六边形ABCDEF内接于$\odot O$,则$\odot O$的圆心角为$360^{\circ}$,每条边所对的圆心角为$360^{\circ}÷6 = 60^{\circ}$,即$\angle COD = 60^{\circ}$。
Q是$\widehat{DE}$的中点,$\widehat{DE}$所对圆心角为$60^{\circ}$,故$\widehat{DQ}=\frac{1}{2}\widehat{DE}$,所对圆心角为$30^{\circ}$,即$\angle DOQ = 30^{\circ}$。
$\angle COQ=\angle COD+\angle DOQ=60^{\circ}+30^{\circ}=90^{\circ}$。
$\angle CPQ$是$\widehat{CQ}$所对的圆周角,$\angle COQ$是$\widehat{CQ}$所对的圆心角,所以$\angle CPQ=\frac{1}{2}\angle COQ=\frac{1}{2}×90^{\circ}=45^{\circ}$。
答案:C
13. 刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,即利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.设半径为1的圆的面积与其内接正n边形的面积差为$△_{n}$,如图①②,若用圆的内接正八边形和内接正十二边形逼近半径为1的圆,则$△_{8}-△_{12}= $
$3 - 2\sqrt{2}$
.
答案:
【解析】:
本题可先分别求出半径为$1$的圆的面积、圆的内接正八边形的面积、圆的内接正十二边形的面积,再根据$\triangle_{n}$的定义求出$\triangle_{8}$和$\triangle_{12}$,最后计算$\triangle_{8}-\triangle_{12}$的值。
半径为$1$的圆的面积$S_{圆}=\pi r^{2}=\pi×1^{2}=\pi$。
求圆的内接正八边形的面积$S_{8}$:
把圆的内接正八边形分成$8$个等腰三角形,每个等腰三角形的顶角为$\frac{360^{\circ}}{8} = 45^{\circ}$,腰长为圆的半径$1$。
根据三角形面积公式$S = \frac{1}{2}ab\sin C$(其中$a,b$为三角形的两边,$C$为$a,b$夹角),可得每个等腰三角形的面积为$\frac{1}{2}×1×1×\sin45^{\circ}=\frac{1}{2}×\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{4}$。
那么圆的内接正八边形的面积$S_{8}=8×\frac{\sqrt{2}}{4}=2\sqrt{2}$。
求圆的内接正十二边形的面积$S_{12}$:
把圆的内接正十二边形分成$12$个等腰三角形,每个等腰三角形的顶角为$\frac{360^{\circ}}{12} = 30^{\circ}$,腰长为圆的半径$1$。
同样根据三角形面积公式,可得每个等腰三角形的面积为$\frac{1}{2}×1×1×\sin30^{\circ}=\frac{1}{2}×\frac{1}{2}=\frac{1}{4}$。
所以圆的内接正十二边形的面积$S_{12}=12×\frac{1}{4}=3$。
根据$\triangle_{n}$的定义求出$\triangle_{8}$和$\triangle_{12}$:
已知半径为$1$的圆的面积与其内接正$n$边形的面积差为$\triangle_{n}$,则$\triangle_{8}=S_{圆}-S_{8}=\pi - 2\sqrt{2}$,$\triangle_{12}=S_{圆}-S_{12}=\pi - 3$。
计算$\triangle_{8}-\triangle_{12}$的值:
$\triangle_{8}-\triangle_{12}=(\pi - 2\sqrt{2})-(\pi - 3)=\pi - 2\sqrt{2}-\pi + 3=3 - 2\sqrt{2}$。
【答案】:$3 - 2\sqrt{2}$
本题可先分别求出半径为$1$的圆的面积、圆的内接正八边形的面积、圆的内接正十二边形的面积,再根据$\triangle_{n}$的定义求出$\triangle_{8}$和$\triangle_{12}$,最后计算$\triangle_{8}-\triangle_{12}$的值。
半径为$1$的圆的面积$S_{圆}=\pi r^{2}=\pi×1^{2}=\pi$。
求圆的内接正八边形的面积$S_{8}$:
把圆的内接正八边形分成$8$个等腰三角形,每个等腰三角形的顶角为$\frac{360^{\circ}}{8} = 45^{\circ}$,腰长为圆的半径$1$。
根据三角形面积公式$S = \frac{1}{2}ab\sin C$(其中$a,b$为三角形的两边,$C$为$a,b$夹角),可得每个等腰三角形的面积为$\frac{1}{2}×1×1×\sin45^{\circ}=\frac{1}{2}×\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{4}$。
那么圆的内接正八边形的面积$S_{8}=8×\frac{\sqrt{2}}{4}=2\sqrt{2}$。
求圆的内接正十二边形的面积$S_{12}$:
把圆的内接正十二边形分成$12$个等腰三角形,每个等腰三角形的顶角为$\frac{360^{\circ}}{12} = 30^{\circ}$,腰长为圆的半径$1$。
同样根据三角形面积公式,可得每个等腰三角形的面积为$\frac{1}{2}×1×1×\sin30^{\circ}=\frac{1}{2}×\frac{1}{2}=\frac{1}{4}$。
所以圆的内接正十二边形的面积$S_{12}=12×\frac{1}{4}=3$。
根据$\triangle_{n}$的定义求出$\triangle_{8}$和$\triangle_{12}$:
已知半径为$1$的圆的面积与其内接正$n$边形的面积差为$\triangle_{n}$,则$\triangle_{8}=S_{圆}-S_{8}=\pi - 2\sqrt{2}$,$\triangle_{12}=S_{圆}-S_{12}=\pi - 3$。
计算$\triangle_{8}-\triangle_{12}$的值:
$\triangle_{8}-\triangle_{12}=(\pi - 2\sqrt{2})-(\pi - 3)=\pi - 2\sqrt{2}-\pi + 3=3 - 2\sqrt{2}$。
【答案】:$3 - 2\sqrt{2}$
查看更多完整答案,请扫码查看


