《2025年金钥匙课时学案作业本九年级数学上册人教版》

1. (2024·天津)如图,在$\triangle ABC$中,$∠B= 30^{\circ }$,将$\triangle ABC$绕点 C 顺时针旋转$60^{\circ }得到\triangle DEC$,点 A,B 的对应点分别为 D,E,延长 BA 交 DE 于点 F,则下列结论一定正确的是 (D)

A.$∠ACB= ∠ACD$
B.$AC// DE$
C.$AB= EF$
D.$BF⊥CE$
]

答案： 【解析】：本题可根据旋转的性质，逐一分析选项。
选项A：判断$\angle ACB$与$\angle ACD$是否相等
已知$\triangle ABC$绕点$C$顺时针旋转$60^{\circ}$得到$\triangle DEC$，则$\angle ACD = 60^{\circ}$，$\angle ACB$的度数不确定，所以$\angle ACB$不一定等于$\angle ACD$，该选项错误。
选项B：判断$AC$与$DE$是否平行
由旋转的性质可知$\angle E = \angle B = 30^{\circ}$，$\angle ACD = 60^{\circ}$，$\angle D = \angle A$。
因为$\triangle ABC$绕点$C$顺时针旋转$60^{\circ}$得到$\triangle DEC$，所以$\angle ACD = 60^{\circ}$，$\angle DCE=\angle ACB$。
又因为$\angle B = 30^{\circ}$，在$\triangle ABC$中，$\angle BAC=180^{\circ}-\angle B - \angle ACB=150^{\circ}-\angle ACB$，$\angle D = \angle A$，所以$\angle D = 150^{\circ}-\angle ACB$。
而$\angle FDC = 180^{\circ}-\angle ADE - \angle ADC$，由旋转可知$\angle ADE = \angle B = 30^{\circ}$，$\angle ADC$与$\angle ACB$相关，可推出$\angle FDC + \angle ACD\neq180^{\circ}$，所以$AC$与$DE$不平行，该选项错误。
选项C：判断$AB$与$EF$是否相等
仅根据已知条件，无法得出$AB$与$EF$的数量关系，该选项错误。
选项D：判断$BF$与$CE$是否垂直
因为$\triangle ABC$绕点$C$顺时针旋转$60^{\circ}$得到$\triangle DEC$，所以$\angle BCE = 60^{\circ}$，$\angle E = \angle B = 30^{\circ}$。
在$\triangle CEF$中，$\angle E = 30^{\circ}$，$\angle ECF = 60^{\circ}$，根据三角形内角和为$180^{\circ}$，可得$\angle EFC = 180^{\circ} - 30^{\circ} - 60^{\circ} = 90^{\circ}$，即$BF\perp CE$，该选项正确。
【答案】：D

2. (2024·滨州)将一副三角尺按如图①所示的方式摆放,把三角尺 AOB 绕公共顶点 O 顺时针旋转至如图②所示的位置$(AB// OD)$,则$∠1$的度数为____.
]
75°

答案： 解：在图①中，三角尺AOB为等腰直角三角形，∠AOB=90°，∠OAB=45°；三角尺COD为含30°角的直角三角形，∠COD=90°，∠ODC=30°，则∠OCD=60°。
在图②中，
∵AB//OD，
∴∠OAB=∠AOD=45°（两直线平行，内错角相等）。
∵∠COD=90°，
∴∠BOC=∠COD - ∠BOD。又
∵∠AOD=∠AOB - ∠BOD=45°，∠AOB=90°，
∴∠BOD=90° - 45°=45°，则∠BOC=90° - 45°=45°。
在△OBC中，∠OCD=60°（对顶角相等），∠BOC=45°，
∴∠1=180° - ∠OCD - ∠BOC=180° - 60° - 45°=75°。
75°

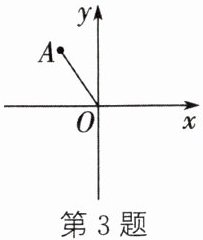
3. (2024·湖北)如图,在平面直角坐标系中,点 A 的坐标为$(-4,6)$,将线段 OA 绕点 O 顺时针旋转$90^{\circ }$,则点 A 的对应点$A'$的坐标为 (B)

A.$(4,6)$
B.$(6,4)$
C.$(-4,-6)$
D.$(-6,-4)$
]

答案： 【解析】：本题考查平面直角坐标系中，绕原点旋转后的点的坐标变化。
点$A$的坐标为$(-4,6)$，将线段$OA$绕点$O$顺时针旋转$90^\circ$，
则点$A$的对应点$A'$的坐标可以通过旋转矩阵或者几何性质来求解。
在平面直角坐标系中，一个点$(x,y)$绕原点顺时针旋转$90^\circ$后的新坐标可以通过旋转矩阵$\begin{bmatrix}0&1\\-1&0\end{bmatrix}$计算得到，
即$(x',y')=(y,-x)$。
应用这个旋转矩阵到点$A(-4,6)$，
得到$A'$的坐标为$(6,4)$。
【答案】：B.$(6,4)$。

4. 如图,点 A 的坐标是$(4,0)$,点 B 的坐标是$(0,3)$,将$\triangle AOB$绕点 B 旋转$90^{\circ }$,则点 A 的对应点$A'$的坐标是____$(3,7)$或$(-3,-1)$.

答案： 1. 首先，计算$OA$和$OB$的长度：
已知$A(4,0)$，$B(0,3)$，根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$（这里$O(0,0)$），可得$OA=\sqrt{(4 - 0)^2+(0 - 0)^2}=4$，$OB=\sqrt{(0 - 0)^2+(3 - 0)^2}=3$。
由勾股定理$AB=\sqrt{OA^{2}+OB^{2}}=\sqrt{4^{2}+3^{2}} = 5$。
2. 然后，分两种情况讨论旋转：
情况一：$\triangle AOB$绕点$B$顺时针旋转$90^{\circ}$：
过$A'$作$A'C\perp y$轴于$C$。
因为$\angle A'BC+\angle ABO = 90^{\circ}$，$\angle BAO+\angle ABO = 90^{\circ}$，所以$\angle A'BC=\angle BAO$。
又因为$\angle A'CB=\angle BOA = 90^{\circ}$，$A'B = AB = 5$，$BO = 3$。
根据$AAS$（角 - 角 - 边）判定$\triangle A'BC\cong\triangle BAO$。
则$A'C = BO = 3$，$BC = OA = 4$。
因为$B(0,3)$，$OC=OB + BC$，所以$OC=3 + 4=7$，此时$A'(3,7)$。
情况二：$\triangle AOB$绕点$B$逆时针旋转$90^{\circ}$：
过$A'$作$A'D\perp y$轴于$D$。
因为$\angle A'BD+\angle A'BC = 90^{\circ}$，$\angle ABO+\angle A'BC = 90^{\circ}$，所以$\angle A'BD=\angle ABO$。
又因为$\angle A'DB=\angle BOA = 90^{\circ}$，$A'B = AB = 5$。
根据$AAS$判定$\triangle A'BD\cong\triangle BAO$。
则$A'D = BO = 3$，$BD = OA = 4$。
因为$B(0,3)$，$OD=BD - OB$，所以$OD = 4 - 3 = 1$，此时$A'(-3,-1)$。
综上，点$A$的对应点$A'$的坐标是$(3,7)$或$(-3,-1)$。

5. 如图,在四边形 ABCD 中,$∠ABC= 90^{\circ },AB= CB,AD= 2,CD= 4$,连接 BD,将线段 BD 绕点 B 逆时针旋转$90^{\circ }得到线段BD'$,连接$DD'$.当$DD'$的长取得最大值时,AB 的长为 (B)
A.3
B.$\sqrt {10}$
C.$\sqrt {11}$
D.$2\sqrt {3}$

答案： B

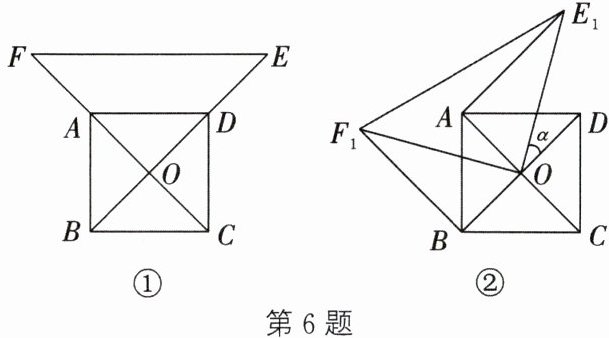
6. 如图①,点 O 为正方形 ABCD 的中心,分别延长 OA,OD 至点 F,E,使$OF= 2OA,OE= 2OD$,连接 EF.将$\triangle EOF$绕点 O 逆时针旋转得到$\triangle E_{1}OF_{1}$,旋转角为α(如图②),连接$AE_{1},BF_{1}.$
(1) 探究$AE_{1}与BF_{1}$之间的数量关系,并加以证明;
(2) 当$α=30^{\circ }$时,求证:$\triangle AOE_{1}$为直角三角形.
]

答案：
(1) $AE_{1}=BF_{1}$。证明：
∵ 点 O 为正方形 ABCD 的中心，
∴ $OA=OB=OD$，$∠AOD=∠AOB=90^{\circ}$。
∵ $OF=2OA$，$OE=2OD$，
∴ $OE=OF$。
∵ $\triangle EOF$ 绕点 O 逆时针旋转得到 $\triangle E_{1}OF_{1}$，
∴ $OE_{1}=OE=OF=OF_{1}$，$∠E_{1}OF_{1}=∠EOF=90^{\circ}$，$∠AOE_{1}=∠AOD - ∠E_{1}OD = 90^{\circ} - ∠E_{1}OD$，$∠BOF_{1}=∠AOB - ∠F_{1}OA = 90^{\circ} - ∠F_{1}OA$，又 $∠E_{1}OD = ∠F_{1}OA$（旋转角相等），
∴ $∠AOE_{1}=∠BOF_{1}$。
在 $\triangle AOE_{1}$ 和 $\triangle BOF_{1}$ 中，$\left\{\begin{array}{l}OA=OB\\∠AOE_{1}=∠BOF_{1}\\OE_{1}=OF_{1}\end{array}\right.$，
∴ $\triangle AOE_{1}≌\triangle BOF_{1}(SAS)$，
∴ $AE_{1}=BF_{1}$。
(2) 证明：
∵ $OE=2OD$，$OD=OA$，
∴ $OE_{1}=OE=2OA$，即 $\frac{OA}{OE_{1}}=\frac{1}{2}$。
∵ $α=30^{\circ}$，$∠AOD=90^{\circ}$，
∴ $∠AOE_{1}=∠AOD - α=90^{\circ}-30^{\circ}=60^{\circ}$。
在 $\triangle AOE_{1}$ 中，设 $OA=x$，则 $OE_{1}=2x$，过点 A 作 $AH⊥OE_{1}$ 于 H，在 $Rt\triangle AOH$ 中，$AH=OA\cdot\sin60^{\circ}=\frac{\sqrt{3}}{2}x$，$OH=OA\cdot\cos60^{\circ}=\frac{1}{2}x$，
∴ $HE_{1}=OE_{1}-OH=2x - \frac{1}{2}x=\frac{3}{2}x$。
在 $Rt\triangle AHE_{1}$ 中，$AE_{1}^{2}=AH^{2}+HE_{1}^{2}=(\frac{\sqrt{3}}{2}x)^{2}+(\frac{3}{2}x)^{2}=\frac{3}{4}x^{2}+\frac{9}{4}x^{2}=3x^{2}$，又 $OA^{2}+AE_{1}^{2}=x^{2}+3x^{2}=4x^{2}=(2x)^{2}=OE_{1}^{2}$，
∴ $\triangle AOE_{1}$ 为直角三角形。