第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
8. 现有4条线段,长度依次是2,4,6,7,从中任选三条,能组成三角形的概率是 (
A.$\frac {1}{4}$
B.$\frac {1}{2}$
C.$\frac {3}{5}$
D.$\frac {3}{4}$
B
)A.$\frac {1}{4}$
B.$\frac {1}{2}$
C.$\frac {3}{5}$
D.$\frac {3}{4}$
答案:
解:从4条线段中任选3条,共有以下4种组合:
①2,4,6;②2,4,7;③2,6,7;④4,6,7。
根据三角形三边关系(任意两边之和大于第三边):
①2+4=6,不满足,不能组成三角形;
②2+4=6<7,不满足,不能组成三角形;
③2+6=8>7,2+7=9>6,6+7=13>2,满足,能组成三角形;
④4+6=10>7,4+7=11>6,6+7=13>4,满足,能组成三角形。
能组成三角形的组合有2种,总组合数为4种,概率为$\frac{2}{4}=\frac{1}{2}$。
答案:B
①2,4,6;②2,4,7;③2,6,7;④4,6,7。
根据三角形三边关系(任意两边之和大于第三边):
①2+4=6,不满足,不能组成三角形;
②2+4=6<7,不满足,不能组成三角形;
③2+6=8>7,2+7=9>6,6+7=13>2,满足,能组成三角形;
④4+6=10>7,4+7=11>6,6+7=13>4,满足,能组成三角形。
能组成三角形的组合有2种,总组合数为4种,概率为$\frac{2}{4}=\frac{1}{2}$。
答案:B
9. 如图所示的方格地面上,标有编号1,2,3的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.一只自由飞翔的小鸟,将随意地落在图中所示的方格地面上,则小鸟落在草坪上的概率是
2/3
.
答案:
解:方格地面共有9个小方格,其中草坪有6个。
小鸟落在草坪上的概率 = 草坪方格数 / 总方格数 = 6 / 9 = 2 / 3。
2/3
小鸟落在草坪上的概率 = 草坪方格数 / 总方格数 = 6 / 9 = 2 / 3。
2/3
10. 圆周率π是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对π有过深入的研究.目前,超级计算机已计算出π的小数部分超过31.4万亿位.有学者发现,随着π小数部分位数的增加,0~9这10个数字出现的频率趋于稳定接近相同.
(1)从π的小数部分随机取出一个数字,估计数字是6的概率为
(2)某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表方法求解)
解:设祖冲之、刘徽、韦达、欧拉分别为A、B、C、D。
随机选用2幅的所有可能情况有:AB, AC, AD, BC, BD, CD,共6种,且每种情况的可能性相同。
其中有一幅是祖冲之的情况有:AB, AC, AD,共3种。
所以,其中有一幅是祖冲之的概率为$\frac{3}{6} = \frac{1}{2}$。
(1)从π的小数部分随机取出一个数字,估计数字是6的概率为
$\frac{1}{10}$(或0.1)
;(2)某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表方法求解)
解:设祖冲之、刘徽、韦达、欧拉分别为A、B、C、D。
随机选用2幅的所有可能情况有:AB, AC, AD, BC, BD, CD,共6种,且每种情况的可能性相同。
其中有一幅是祖冲之的情况有:AB, AC, AD,共3种。
所以,其中有一幅是祖冲之的概率为$\frac{3}{6} = \frac{1}{2}$。
答案:
【解析】:
(1) 本题考查概率的基本概念。由于π是一个无限不循环小数,且随着小数部分的增加,0~9这10个数字出现的频率趋于稳定并接近相同,因此从π的小数部分随机取出一个数字,每个数字出现的概率应相等。所以,数字是6的概率为$\frac{1}{10}$,即$0.1$。
(2) 本题考查利用树状图或列表法求概率。设祖冲之、刘徽、韦达、欧拉分别为A、B、C、D。我们可以列出所有可能的组合情况,然后计算其中包含祖冲之(A)的组合所占的比例。
首先,我们画出树状图或列表来表示所有可能的组合:
AB, AC, AD, BC, BD, CD
然后,我们计算总组合数为6(从4位科学家中选2位),并找出包含A的组合数,即AB, AC, AD,共3种。
所以,其中有一幅是祖冲之的概率为$\frac{3}{6} = \frac{1}{2}$。
【答案】:
(1) $0.1$(或 $\frac{1}{10}$)
(2) 解:设祖冲之、刘徽、韦达、欧拉分别为A、B、C、D。
随机选用2幅的所有可能情况有:AB, AC, AD, BC, BD, CD,共6种,且每种情况的可能性相同。
其中有一幅是祖冲之的情况有:AB, AC, AD,共3种。
所以,其中有一幅是祖冲之的概率为$\frac{3}{6} = \frac{1}{2}$。
(1) 本题考查概率的基本概念。由于π是一个无限不循环小数,且随着小数部分的增加,0~9这10个数字出现的频率趋于稳定并接近相同,因此从π的小数部分随机取出一个数字,每个数字出现的概率应相等。所以,数字是6的概率为$\frac{1}{10}$,即$0.1$。
(2) 本题考查利用树状图或列表法求概率。设祖冲之、刘徽、韦达、欧拉分别为A、B、C、D。我们可以列出所有可能的组合情况,然后计算其中包含祖冲之(A)的组合所占的比例。
首先,我们画出树状图或列表来表示所有可能的组合:
AB, AC, AD, BC, BD, CD
然后,我们计算总组合数为6(从4位科学家中选2位),并找出包含A的组合数,即AB, AC, AD,共3种。
所以,其中有一幅是祖冲之的概率为$\frac{3}{6} = \frac{1}{2}$。
【答案】:
(1) $0.1$(或 $\frac{1}{10}$)
(2) 解:设祖冲之、刘徽、韦达、欧拉分别为A、B、C、D。
随机选用2幅的所有可能情况有:AB, AC, AD, BC, BD, CD,共6种,且每种情况的可能性相同。
其中有一幅是祖冲之的情况有:AB, AC, AD,共3种。
所以,其中有一幅是祖冲之的概率为$\frac{3}{6} = \frac{1}{2}$。
11. 已知a、b可以取-2,-1,1,2中任意一个值$(a≠b)$,则直线$y= ax+b$不经过第四象限的概率是
$\frac{1}{6}$
.
答案:
解:
1. 确定所有可能的直线:
a、b取值于{-2,-1,1,2}且a≠b,共有4×3=12种组合,对应12条直线。
2. 直线不经过第四象限的条件:
需满足a>0且b≥0。
3. 符合条件的(a,b)组合:
a=1时,b=2;a=2时,b=1。共2种。
4. 计算概率:
概率=符合条件的组合数/总组合数=2/12=1/6。
答案:$\frac{1}{6}$
1. 确定所有可能的直线:
a、b取值于{-2,-1,1,2}且a≠b,共有4×3=12种组合,对应12条直线。
2. 直线不经过第四象限的条件:
需满足a>0且b≥0。
3. 符合条件的(a,b)组合:
a=1时,b=2;a=2时,b=1。共2种。
4. 计算概率:
概率=符合条件的组合数/总组合数=2/12=1/6。
答案:$\frac{1}{6}$
12. 九年级(1)班针对“垃圾分类”知晓情况对全班学生进行专题调查活动,对“垃圾分类”的知晓情况分为A、B、C、D四类.其中,A类表示“非常了解”;B类表示“比较了解”;C类表示“基本了解”;D类表示“不太了解”,每名学生可根据自己的情况任选其中一类,班长对调查结果进行了统计,并绘制成了不完整的条形统计图和扇形统计图.
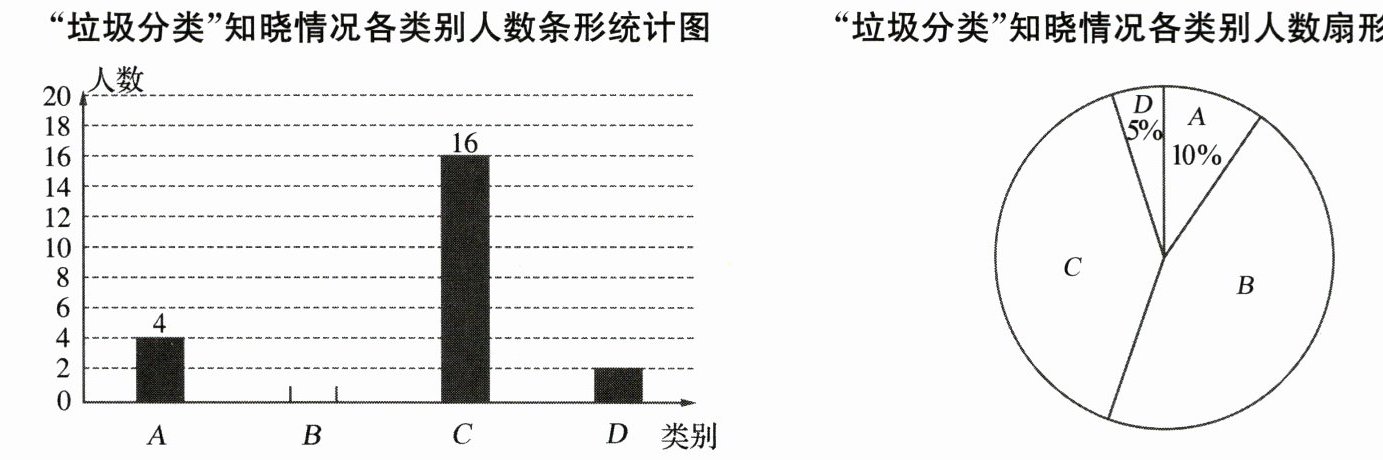
根据以上信息解答下列问题:
(1)九年级(1)班参加这次调查的学生有
(2)求出类别B的学生数,并补全条形统计图;
(3)类别A的4名学生中有2名男生和2名女生,现从这4名学生中随机选取2名学生参加学校“垃圾分类”知识竞赛,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.

根据以上信息解答下列问题:
(1)九年级(1)班参加这次调查的学生有
40
人,扇形统计图中类别C所对应扇形的圆心角度数为144°
;(2)求出类别B的学生数,并补全条形统计图;
解:B类学生数为40 - 4 - 16 - 2 = 18(人),补全条形统计图略
(3)类别A的4名学生中有2名男生和2名女生,现从这4名学生中随机选取2名学生参加学校“垃圾分类”知识竞赛,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
解:列表如下:
| | 男1 | 男2 | 女1 | 女2 |
| --- | --- | --- | --- | --- |
| 男1 | - | (男1,男2) | (男1,女1) | (男1,女2) |
| 男2 | (男2,男1) | - | (男2,女1) | (男2,女2) |
| 女1 | (女1,男1) | (女1,男2) | - | (女1,女2) |
| 女2 | (女2,男1) | (女2,男2) | (女2,女1) | - |
共有12种等可能结果,其中1男1女的结果有8种,
∴P(1男1女)=8/12=2/3
| | 男1 | 男2 | 女1 | 女2 |
| --- | --- | --- | --- | --- |
| 男1 | - | (男1,男2) | (男1,女1) | (男1,女2) |
| 男2 | (男2,男1) | - | (男2,女1) | (男2,女2) |
| 女1 | (女1,男1) | (女1,男2) | - | (女1,女2) |
| 女2 | (女2,男1) | (女2,男2) | (女2,女1) | - |
共有12种等可能结果,其中1男1女的结果有8种,
∴P(1男1女)=8/12=2/3
答案:
(1)40;144°
(2)解:B类学生数为40 - 4 - 16 - 2 = 18(人),补全条形统计图略
(3)解:列表如下:
| | 男1 | 男2 | 女1 | 女2 |
| --- | --- | --- | --- | --- |
| 男1 | - | (男1,男2) | (男1,女1) | (男1,女2) |
| 男2 | (男2,男1) | - | (男2,女1) | (男2,女2) |
| 女1 | (女1,男1) | (女1,男2) | - | (女1,女2) |
| 女2 | (女2,男1) | (女2,男2) | (女2,女1) | - |
共有12种等可能结果,其中1男1女的结果有8种,
∴P(1男1女)=8/12=2/3
(1)40;144°
(2)解:B类学生数为40 - 4 - 16 - 2 = 18(人),补全条形统计图略
(3)解:列表如下:
| | 男1 | 男2 | 女1 | 女2 |
| --- | --- | --- | --- | --- |
| 男1 | - | (男1,男2) | (男1,女1) | (男1,女2) |
| 男2 | (男2,男1) | - | (男2,女1) | (男2,女2) |
| 女1 | (女1,男1) | (女1,男2) | - | (女1,女2) |
| 女2 | (女2,男1) | (女2,男2) | (女2,女1) | - |
共有12种等可能结果,其中1男1女的结果有8种,
∴P(1男1女)=8/12=2/3
查看更多完整答案,请扫码查看


