《2025年创新课时作业本九年级数学上册苏州专版》

1. 连接圆上任意两点的线段叫作弦,经过圆心的弦叫作直径.
2. 圆上任意两点间的部分叫作圆弧,圆的任意一条直径的两个端点分圆成两条弧,每条弧都叫作半圆,大于半圆的弧叫作优弧,小于半圆的弧叫作劣弧.
3. 顶点在圆心的角叫作圆心角,圆心相同半径不等的两个圆叫作同心圆；能够互相重合的两个圆叫作等圆；能够互相重合的弧叫作等弧；
4. 同圆或等圆的半径相等.

答案： 【解析】：
本题主要考查了圆的基本概念，包括弦、直径、圆弧、半圆、优弧、劣弧、圆心角、同心圆、等圆、等弧以及同圆或等圆的半径等知识点。这些概念是学习圆的相关知识的基础，需要准确理解和记忆。
【答案】：
1. 连接圆上任意两点的线段叫作弦，经过圆心的弦叫作直径。
2. 圆上任意两点间的部分叫作圆弧，圆的任意一条直径的两个端点分圆成两条弧，每条弧都叫作半圆，大于半圆的弧叫作优弧，小于半圆的弧叫作劣弧。
3. 顶点在圆心的角叫作圆心角，圆心相同半径不等的两个圆叫作同心圆；能够互相重合的两个圆叫作等圆；能够互相重合的弧叫作等弧。
4. 同圆或等圆的半径相等。

1. 有下列说法：①相等的圆心角所对的弧相等；②半圆是弧；③长度相等的两条弧是等弧；④经过圆心的每一条直线都是圆的对称轴. 其中正确的有(B)
A.1个
B.2个
C.3个
D.4个

答案： 【解析】：
本题主要考查了圆的基本性质，包括圆心角与弧的关系、半圆与弧的定义、等弧的定义以及圆的对称轴。
① 根据圆的性质，我们知道，在同圆或等圆中，相等的圆心角所对的弧是相等的。但题目中只提到了“相等的圆心角所对的弧相等”，没有提到“在同圆或等圆中”，因此此说法是错误的。
② 半圆实际上是圆的一半，它确实是一种特殊的弧，所以此说法是正确的。
③ 等弧的定义是在同圆或等圆中，能够完全重合的两条弧。但题目中只提到了“长度相等的两条弧是等弧”，没有提到“在同圆或等圆中”，因此此说法是错误的。
④ 根据圆的对称性，我们知道，经过圆心的任意一条直线都可以将圆分成两个完全对称的部分，因此此说法是正确的。
综上，正确的说法有2个。
【答案】：
B

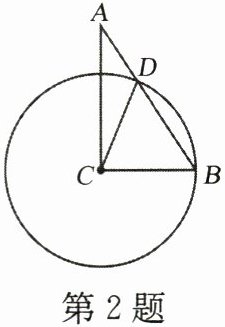
2. 如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$\angle A= 40^{\circ}$,以点$C$为圆心,$CB为半径的圆交AB于点D$,连接$CD$,则$\angle ACD$的度数为(A)

A.$10^{\circ}$
B.$15^{\circ}$
C.$20^{\circ}$
D.$25^{\circ}$

答案： 解：在$\triangle ABC$中，$\angle ACB=90^{\circ}$，$\angle A=40^{\circ}$，
$\angle B=180^{\circ}-\angle ACB-\angle A=180^{\circ}-90^{\circ}-40^{\circ}=50^{\circ}$。
因为$CB=CD$，
所以$\triangle CBD$是等腰三角形，$\angle CDB=\angle B=50^{\circ}$。
$\angle BCD=180^{\circ}-\angle CDB-\angle B=180^{\circ}-50^{\circ}-50^{\circ}=80^{\circ}$。
$\angle ACD=\angle ACB-\angle BCD=90^{\circ}-80^{\circ}=10^{\circ}$。
答案：A

3. 如图,点$M$、$G$、$D在半圆O$上,四边形$OEDF$、四边形$HMNO$均为矩形,$EF = b$,$NH = c$,则$b与c$之间的大小关系是(B)
A.$b＞c$
B.$b = c$
C.$c＞b$
D.$b与c$的大小不能确定

答案： 解：连接OD、OM。
∵四边形OEDF是矩形，
∴EF=OD（矩形对角线相等）。
∵点D在半圆O上，
∴OD是半圆O的半径，设OD=R，则EF=b=R。
∵四边形HMNO是矩形，
∴NH=OM（矩形对角线相等）。
∵点M在半圆O上，
∴OM是半圆O的半径，即OM=R，则NH=c=R。
∴b=c。
答案：B

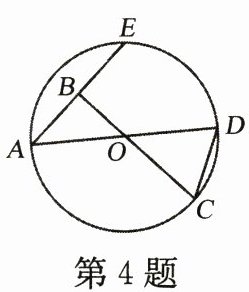
4. 如图所示的$\odot O$中有3条弦,以$A$为端点的优弧有2条.

答案： 3,2

5. 如图,$AB是\odot O$的直径,$D是AC$的中点,若$BC = 8\mathrm{cm}$,则$OD = $4$\mathrm{cm}$.

答案： 【解析】：本题主要考查圆的性质及三角形中位线的性质。
先明确圆的直径所对的圆周角是直角这一性质，得出$\bigtriangleup ABC$是直角三角形。
再根据$D$是$AC$中点，$O$是$AB$中点，利用三角形中位线定理求出$OD$的长度。
连接$OC$。
因为$AB$是$\odot O$的直径，根据直径所对的圆周角是直角，所以$\angle ACB = 90^{\circ}$。
因为$D$是$AC$的中点，$O$是$AB$的中点，在$\bigtriangleup ABC$中，$OD$是中位线。
根据三角形中位线定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半。
所以$OD=\frac{1}{2}BC$。
已知$BC = 8cm$，则$OD=\frac{1}{2}×8 = 4cm$。
【答案】：$4$

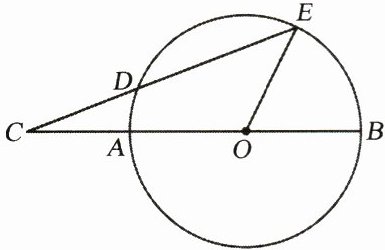
6. 如图,$AB是\odot O$的直径,$C是BA$延长线上一点,点$D在\odot O$上,且$CD = OA$,$CD的延长线交\odot O于点E$. 若$\angle C = 20^{\circ}$,求$\angle BOE$的度数.

答案： 解：连接OD。
∵AB是⊙O的直径，
∴OA=OD=OE=OB（同圆半径相等）。
∵CD=OA，
∴CD=OD（等量代换）。
∴∠C=∠DOC（等边对等角）。
∵∠C=20°，
∴∠DOC=20°。
∵∠ODE是△COD的外角，
∴∠ODE=∠C+∠DOC=20°+20°=40°。
∵OD=OE，
∴∠ODE=∠E=40°（等边对等角）。
∵∠BOE是△COE的外角，
∴∠BOE=∠C+∠E=20°+40°=60°。
答：∠BOE的度数为60°。

7. 如图,$AB$、$CD为\odot O$中两条直径,点$E$、$F在直径CD$上,且$CE = DF$.
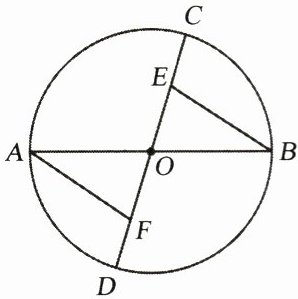
求证：$AF// BE$.

答案： 证明：
∵AB、CD为⊙O的直径，
∴OA=OB，OC=OD。
∵CE=DF，
∴OC-CE=OD-DF，即OE=OF。
在△AOF和△BOE中，
OA=OB，
∠AOF=∠BOE（对顶角相等），
OF=OE，
∴△AOF≌△BOE（SAS）。
∴∠OAF=∠OBE。
∴AF//BE（内错角相等，两直线平行）。