《2025年创新课时作业本九年级数学上册苏州专版》

8. 若$\odot O$所在平面上的一点P到$\odot O$上的点的最大距离是10,最小距离是2,则此圆的半径为 (C)
A.6
B.4
C.6或4
D.12或8

答案： 【解析】：
本题主要考查了圆的基本性质以及点到圆上距离的最大值和最小值与圆的半径之间的关系。
设圆心$O$到点$P$的距离为$d$，圆的半径为$r$。
当点$P$在圆外时，点$P$到圆上的最大距离是$d+r$，最小距离是$d-r$。
根据题意，我们有：
$d + r = 10$。
$d - r = 2$。
解这个方程组，我们得到：
$r = \frac{10 - 2}{2} = 4$。
当点$P$在圆内时，点$P$到圆上的最大距离是$d+r$，而最小距离是$r-d$（此时$d$是圆心到点$P$的距离，因此最小距离是半径减去这个距离）。
根据题意，我们有：
$d + r = 10$。
$r - d = 2$。
解这个方程组，我们得到：
$r = \frac{10 + 2}{2} = 6$。
综合以上两种情况，我们得出圆的半径$r$可以是$6$或$4$。
【答案】：
C. $6$或$4$。

9. (1) 已知$\odot O$的半径为1,点P与圆心O的距离d,且方程$x^{2}-2x+d= 0$没有实数根,则点P在$\odot O$外(填“内”“外”或“上”).
(2) $\odot O$的半径为R,圆心O到点A的距离为d,且R、d分别是方程$x^{2}-4x+4= 0$的两根,则点A与$\odot O$的位置关系是上.

答案： 【解析】：
本题主要考查了圆的性质以及一元二次方程的判别式与解的关系。
(1) 对于方程$x^{2} - 2x + d = 0$，其判别式为$\Delta = b^{2} - 4ac = (-2)^{2} - 4 × 1 × d = 4 - 4d$。
由于方程没有实数根，所以$\Delta ＜ 0$，即$4 - 4d ＜ 0$，解得$d ＞ 1$。
因为$\odot O$的半径为1，且点P到圆心O的距离$d ＞ 1$，所以点P在$\odot O$外。
(2) 对于方程$x^{2} - 4x + 4 = 0$，
因式分解可得$(x-2)^{2} = 0$，
解得$x_{1} = x_{2} = 2$。
由于R、d分别是方程的两根，所以$R = d = 2$（由于半径不能为负或零，这里只取正值）。
因为$\odot O$的半径R等于点A到圆心O的距离d，所以点A在$\odot O$上。
【答案】：
(1) 外
(2) 上

10. 如图,有A、B、C三个村庄,A庄在某市的市中心O正南方40 km处,B、C两个村庄在A庄的正东方向上,且距A庄分别为30 km和35 km,该市中心有一座信息发射塔(即点O),覆盖半径为50 km. 三个村庄A、B、C是否能收到该塔发出的信息?

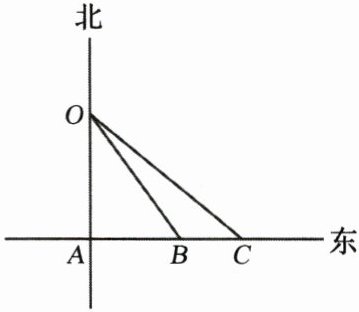
答案： 【解析】：
本题主要考查了勾股定理的应用以及点与圆的位置关系。
在直角三角形中，利用勾股定理求出$OB$，$OC$的长度，已知发射塔的覆盖半径，通过比较$OB$，$OC$与覆盖半径的大小关系，从而判断三个村庄是否能收到信息。
已知$A$庄在市中心$O$正南方$40km$处，即$OA = 40km$，$B$庄在$A$庄正东方向且距$A$庄$30km$，$C$庄在$A$庄正东方向且距$A$庄$35km$。
在$Rt\bigtriangleup OAB$中，根据勾股定理$a^2 + b^2 = c^2$（其中$a$、$b$为直角边，$c$为斜边），这里$OA$和$AB$为直角边，$OB$为斜边，则$OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{40^{2}+30^{2}} = 50(km)$。
在$Rt\bigtriangleup OAC$中，$OA$和$AC$为直角边，$OC$为斜边，则$OC=\sqrt{OA^{2}+AC^{2}}=\sqrt{40^{2}+35^{2}}=\sqrt{1600 + 1225}=\sqrt{2825}\approx53.15(km)$。
已知信息发射塔覆盖半径为$50km$，$OB = 50km$，说明$B$庄刚好在覆盖范围内，能收到信息；$OC\approx53.15km＞50km$，说明$C$庄不在覆盖范围内，不能收到信息；$OA = 40km＜50km$，说明$A$庄在覆盖范围内，能收到信息。
【答案】：
$A$，$B$两个村庄能收到该塔发出的信息，$C$村庄不能收到该塔发出的信息。

11. 如图,$\odot A$的半径为2,圆心A的坐标为$(-3,4)$,P是$\odot A$上的运动点,则点P到点O的最大距离为7.

答案： 【解析】：本题考查圆的性质以及点与圆的位置关系，需要先明确点$O$的坐标，再结合圆的半径求出点$P$到点$O$的最大距离。
在平面直角坐标系中，点$O$为坐标原点，其坐标为$(0,0)$。
已知圆心$A$的坐标为$(-3,4)$，$\odot A$的半径为$2$，点$P$是$\odot A$上的动点。
根据圆的性质，圆上一点到圆外一点的距离最大值为圆心到该点的距离加上圆的半径。
所以要求点$P$到点$O$的最大距离，需要先求出圆心$A$到点$O$的距离$OA$，再加上圆的半径$r = 2$。
根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$（其中$(x_1,y_1)$，$(x_2,y_2)$为两点的坐标，$d$为两点间的距离），对于点$O(0,0)$和点$A(-3,4)$，有：
$OA=\sqrt{(-3 - 0)^2 + (4 - 0)^2}=\sqrt{(-3)^2 + 4^2}=\sqrt{9 + 16}=\sqrt{25}=5$
则点$P$到点$O$的最大距离为$OA + r = 5 + 2 = 7$。
【答案】：$7$

12. 如图,已知等腰直角三角形ABO放置在平面直角坐标系中,$OA= OB= 4$,以点B为圆心,2为半径作圆,C为圆上的任意一点,连接AC,点M为线段AC的中点,连接OM,则OM的最小值为____.

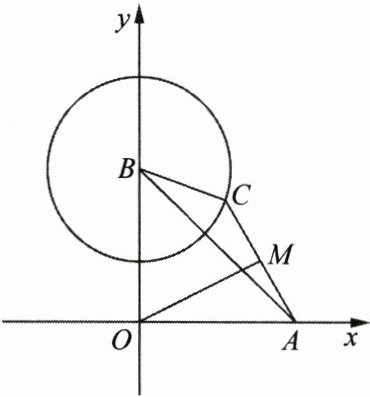
$2\sqrt{2}-1$

答案： 【解析】：本题考查了等腰直角三角形的性质，三角形的中位线定理，以及点与圆的位置关系。
首先，我们明确题目给出的条件：等腰直角三角形$ABO$中，$OA=OB=4$，以点B为圆心，2为半径作圆，C为圆上的任意一点，连接AC，点M为线段AC的中点，连接OM。我们的目标是求出OM的最小值。
取AB的中点D，连接MD，OD。
由于点M是AC的中点，点D是AB的中点。
根据三角形的中位线定理，我们知道中位线的长度是与之平行的那一边的一半，所以$MD=\frac{1}{2}BC$。
又因为以点B为圆心，2为半径作圆，C为圆上的任意一点，所以$BC=2$，那么$MD=1$。
在等腰直角三角形$ABO$中，$OA=OB=4$，点D是AB的中点，所以$OD=\frac{1}{2}AB=2\sqrt{2}$。
接下来，我们考虑点M，D，O三点共线的情况。
由于$OM=OD-MD$（当M，D，O三点共线时取等号），所以当$OM$最小时，$M$，$D$，$O$三点应该共线。
此时，$OM$的最小值就是$OD$减去$MD$，即$OM_{min}=2\sqrt{2}-1$。
【答案】：$2\sqrt{2}-1$。