《2025年创新课时作业本九年级数学上册苏州专版》

8. 如图,等边三角形ABC是由9个大小相等的等边三角形构成,随机地往△ABC内投一粒米,落在阴影区域的概率为$\frac{5}{9}$.

答案： 解：设每个小等边三角形的面积为1，则△ABC的面积为9。由图可知，阴影区域由5个小等边三角形组成，其面积为5。所以随机投一粒米落在阴影区域的概率为阴影区域面积与△ABC面积之比，即$\frac{5}{9}$。
$\frac{5}{9}$

9. 如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是$\frac{6}{25}$.

答案： 解：设每个小正方形的边长为1，则每个小正方形的面积为1。
游戏板是边长为5的正方形，总面积为5×5=25。
黑色区域为三角形，通过数格子或坐标法可得其底为4，高为3，面积为$\frac{1}{2}×4×3=6$。
击中黑色区域的概率是$\frac{6}{25}$。
答案：$\frac{6}{25}$

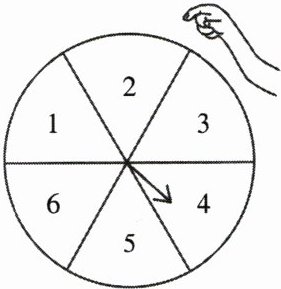
10. 如图,转盘被等分成六个扇形,并在上面依次写上数字1,2,3,4,5,6.
(1) 若自由转动转盘,当它停止转动时,指针指向奇数区域的概率是多少?
(2) 请你用这个转盘设计一个游戏,当自由转动的转盘停止时,指针指向的区域的概率为$\frac {2}{3}$.

答案：
(1)解：转盘被等分成6个扇形，其中奇数区域为1,3,5，共3个。
P(指针指向奇数区域)=$\frac{3}{6}=\frac{1}{2}$。
(2)解：游戏规则：自由转动转盘，当它停止转动时，指针指向的数字小于5的区域。
理由：数字小于5的区域为1,2,3,4，共4个。
P(指针指向数字小于5的区域)=$\frac{4}{6}=\frac{2}{3}$。

11. 汉代数学家赵爽在注解《周牌算经》时给出的"赵爽弦图"是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形均全等,两条直角边之比均为$1:2$.若向该图形内随机投掷一枚小针,则针尖落在阴影区域的概率为____$\frac{1}{5}$.

答案： 【解析】：
本题可先设出直角三角形的两条直角边的长度，然后分别计算出大正方形的面积和阴影部分（小正方形）的面积，最后根据几何概率公式求出针尖落在阴影区域的概率。
步骤一：设未知数并表示出相关线段的长度
设直角三角形的较短的直角边为$x$，因为两个直角边之比为$1:2$，所以较长的直角边为$2x$。
步骤二：计算大正方形的面积
大正方形的边长等于直角三角形的斜边长度，根据勾股定理$a^2 + b^2 = c^2$（其中$a$、$b$为直角边，$c$为斜边），可得大正方形的边长为$\sqrt{x^{2}+(2x)^{2}}=\sqrt{x^{2}+4x^{2}}=\sqrt{5x^{2}}=\sqrt{5}x$。
根据正方形面积公式$S = a^2$（其中$S$为面积，$a$为边长），可得大正方形的面积$S_{大}=(\sqrt{5}x)^{2}=5x^{2}$。
步骤三：计算阴影部分（小正方形）的面积
阴影部分是小正方形，其边长等于直角三角形两条直角边的差，即$2x - x = x$。
根据正方形面积公式，可得阴影部分的面积$S_{阴}=x^{2}$。
步骤四：根据几何概率公式计算针尖落在阴影区域的概率
几何概率公式为$P(A)=\frac{构成事件A的区域长度(面积或体积)}{试验的全部结果所构成的区域长度(面积或体积)}$，设“针尖落在阴影区域”为事件$A$，则针尖落在阴影区域的概率$P(A)=\frac{S_{阴}}{S_{大}}=\frac{x^{2}}{5x^{2}}=\frac{1}{5}$。
【答案】：$\frac{1}{5}$

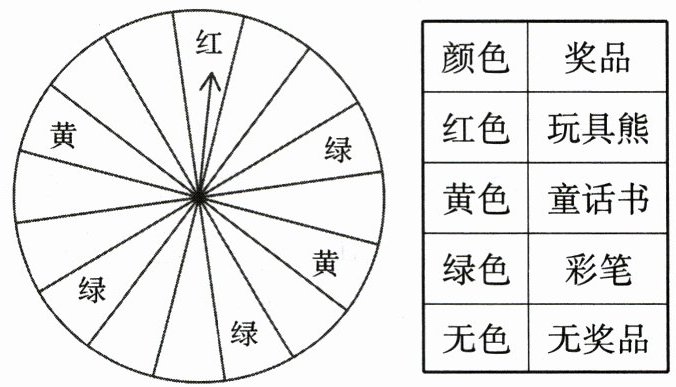
12. “六一”儿童节期间,某商厦为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准哪个区域,顾客就可以获得相应的奖品.小明和妈妈购买了125元的商品,请你分析计算:
(1) 小明获得奖品的概率是多少?
(2) 小明获得童话书的概率是多少?

答案： 【解析】：本题主要考查了概率的计算。
（1）首先，需要确定转盘上有颜色区域的总数以及有奖品的区域数。
转盘被平均分成$16$份，其中$16$个区域都有颜色（红色、黄色、绿色），而根据规定，只有红色、黄色、绿色区域对应有奖品。
因此，有奖品的区域数是$1+2+3=6$(个)（红色$1$个，黄色$2$个，绿色$3$个）。
所以，小明获得奖品的概率$P$(获得奖品)$=\frac{\text{有奖品的区域数}}{\text{总区域数}}=\frac{6}{16}=\frac{3}{8}$。
（2）接下来，分析小明获得童话书的概率。
根据转盘上的标注，黄色区域对应的是童话书，而黄色区域有$2$个。
因此，小明获得童话书的概率$P$(获得童话书)$=\frac{\text{黄色区域数}}{\text{总区域数}}=\frac{2}{16}=\frac{1}{8}$。
【答案】：（1）$\frac{3}{8}$；（2）$\frac{1}{8}$。