《2025年创新课时作业本九年级数学上册苏州专版》

商品销售问题中的常用等量关系:(1) 每件商品的利润= 每件商品的售价-每件商品的进价.(2) 总利润= 每件商品的利润×销售量.

答案： 【解析】：
本题考查了商品销售问题中的常用等量关系。在商品销售问题中，有两个关键的等量关系需要掌握。一是每件商品的利润，它等于每件商品的售价减去每件商品的进价；二是总利润，它等于每件商品的利润乘以销售量。
(1) 对于第一个空，我们需要找到每件商品的利润的计算方式。根据等量关系，每件商品的利润是其售价减去进价。因此，第一个空应填“售价”。
(2) 对于第二个空，我们需要找到总利润的计算方式。根据等量关系，总利润是每件商品的利润乘以销售量。在这个问题中，已经给出了“每件商品的利润”这一部分，所以第二个空应填“利润”。
【答案】：
(1) 售价
(2) 利润

1. 光彩市场某个体商户购进某种电子产品的进价是 50 元/个,根据市场调研发现售价是 80 元/个时,每周可卖出 160 个. 若销售单价每个降低 2 元,则每周可多卖出 20 个;若商户计划下周利润达到 5200 元,则此电子产品的售价为每个多少元? 设销售价格每个降低 x 元(x 为偶数),则所列方程为 (C)
A.$(80-x)(160+20x)= 5200$
B.$(30-x)(160+20x)= 5200$
C.$(30-x)(160+10x)= 5200$
D.$(50-x)(160+10x)= 5200$

答案： 【解析】：
首先，我们确定每个电子产品的初始利润。
进价是$50$元/个，初始售价是$80$元/个，
所以初始利润是$80-50=30$元/个。
若销售价格降低$x$元，则新的售价是$80-x$元/个，
新的利润就是$(80-x)-50=30-x$元/个。
接下来，我们确定销售数量与销售价格的关系。
初始销售数量是$160$个/周。
题目中说，若销售单价每个降低$2$元，则每周可多卖出$20$个。
因此，如果销售价格降低$x$元，销售数量就是$160+\frac{x}{2} × 20 = 160+10x$个/周（因为$x$是偶数，所以$\frac{x}{2}$是整数，表示降低的价格可以整除$2$元，从而对应到增加的销售数量）。
最后，我们根据计划利润来列方程。
计划利润是$5200$元，所以方程就是新的单个利润乘以新的销售数量，
即$(30-x)(160+10x)=5200$。
【答案】：
C.$(30-x)(160+10x)= 5200$。

2. 某超市在销售中发现龙牌童装平均每天可售出 20 件,每件盈利 40 元. 经市场调查发现:如果每件童装每降价 1 元,那么平均每天就可多售出 2 件. 要想平均每天销售这种童装能盈利 1200 元,那么每件童装应降价 (D)
A.10 元
B.20 元
C.30 元
D.10 元或 20 元

答案： 【解析】：
本题主要考察一元二次方程的建立与求解。
首先，我们设每件童装应降价$x$元。
原来的盈利是每件40元，降价后每件盈利就是$40-x$元。
原来每天售出20件，降价后每天多售出$2x$件，所以降价后每天售出$20+2x$件。
因此，降价后的每天盈利就是$(20+2x)(40-x)$元。
根据题意，我们需要这个盈利等于1200元，所以有方程：
$(20+2x)(40-x) = 1200$
展开方程得：
$800 - 20x + 80x - 2x^2 = 1200$
整理得：
$2x^2 - 60x + 400 = 0$
除以2得：
$x^2 - 30x + 200 = 0$
因式分解得：
$(x-10)(x-20) = 0$
解得：
$x_1 = 10, \quad x_2 = 20$
所以，每件童装应降价10元或20元。
【答案】：
D. 10元或20元。

3. 某市青少年校园足球联赛采用单循环制,即每支球队必须和其余球队比赛一场,现有校园足球联赛队伍支,共比赛了 36 场,则下列方程中正确的是 (C)
A.$x(x-1)= 36$
B.$x(x+1)= 36$
C.$\frac{1}{2}x(x-1)= 36$
D.$\frac{1}{2}x(x+1)= 36$

答案： 【解析】：
这是一个关于组合的问题，需要从x支球队中任选2队进行比赛。
组合公式为$C_n^m = \frac{n!}{m!(n-m)!}$，在这里$n=x$，$m=2$，所以比赛场数就是$C_x^2$。
$C_x^2=\frac{x!}{2!(x-2)!} = \frac{x(x-1)}{2}$。
根据题意，这个场数等于36，所以我们有方程：
$\frac{1}{2}x(x-1) = 36$。
【答案】：
C.$\frac{1}{2}x(x-1)= 36$。

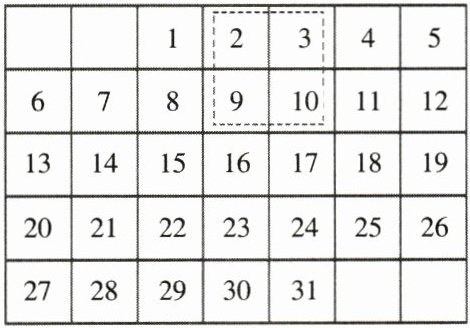
4. 如图为 2018 年的 5 月的月历,在此月历上任意圈出 $2×2$ 个数组成一个正方形,它们组成正方形(如 2,3,9,10),如果圈出的四个数中最小数与最大数的积为 128,这四个数的和为____.

48

答案： 解：设最小数为$x$，则另外三个数分别为$x + 1$，$x + 7$，$x + 8$。
根据题意，得$x(x + 8) = 128$，
整理，得$x^2 + 8x - 128 = 0$，
解得$x_1 = 8$，$x_2 = -16$（不合题意，舍去）。
所以这四个数分别为$8$，$9$，$15$，$16$，
它们的和为$8 + 9 + 15 + 16 = 48$。
答案：$48$

5. 平遥牛肉是我国美食文化的精华之一. 已知某专卖店平遥牛肉的进价为每份 10 元,现在的售价是每份 16 元,每天可卖出 120 份.据市场调查,每涨价 1 元,每天要少卖出 10 份. 如果专卖店每天要想获得 770 元的利润,且要尽可能的让利给顾客,那么售价应涨价1元.

答案： 解：设售价应涨价$x$元。
根据题意，得$(16 + x - 10)(120 - 10x) = 770$
整理，得$x^2 - 6x - 11 = 0$
解得$x_1 = 7$，$x_2 = -1$（不合题意，舍去）
因为要尽可能让利给顾客，所以$x = 1$
答：售价应涨价$1$元。

6. 某商店将进价为 8 元的商品按每件 10 元出售,每天可销售 200 件,现商家采用提高售价,减少进货量的方法增加利润,如果这种商品每件涨 0.5 元,其每天的销量就会减少 10 件. 那么要使每天的利润为 640 元,需将售价定为多少元?

答案： 【解析】：
本题主要考察一元二次方程的应用，特别是在实际问题中如何建立方程并求解。
首先，我们需要确定商品的售价和销量之间的关系。
根据题意，商品每涨价$0.5$元，销量减少$10$件。
设售价为$x$元，则相对于原价$10$元，涨价了$x-10$元。
因此，销量减少的件数为$\frac{x - 10}{0.5} × 10 = 20(x - 10)$。
所以，每天的销售量为$200 - 20(x - 10)$件。
每件的利润为售价减去进价，即$x - 8$元。
因此，每天的总利润为单件利润乘以销售量，即$(x - 8)[200 - 20(x - 10)]$。
根据题意，这个总利润需要等于$640$元，所以我们有方程：
$(x - 8)[200 - 20(x - 10)] = 640$
展开并整理得：
$x^2 - 28x + 192 = 0$
接下来，我们解这个一元二次方程。
因为$\Delta = (-28)^2 - 4 × 1 × 192 = 400 ＞ 0$，方程有两个不相等的实数根。
利用求根公式，我们可以得到：
$x_1 = \frac{28 + \sqrt{400}}{2} = 16, \quad x_2 = \frac{28 - \sqrt{400}}{2} = 12$
【答案】：
需将售价定为$16$元或$12$元。

7. G 旅行社为吸引市民组团去 A 风景区旅游,推出了如下收费标准:如果人数不超过 25 人,人均旅游费用为 1000 元;如果人数超过 25 人,每增加 1 人,人均旅游费用降低 20 元,但人均旅游费用不得低于 700 元. 某单位组织员工去 A 风景区旅游,共支付给 G 旅行社旅游费用 27520 元,单位这次共有多少名员工去 A 风景区旅游?

答案： 【解析】：
本题主要考察一元二次方程的建立与求解。需要根据题目中的条件，设立合适的一元二次方程，并考虑到人均费用不低于700元的限制。
设参加旅游的员工数为$x$人。
当$x \leq 25$时，总费用为$1000x$，但由题意知$1000 × 25 = 25000$，而实际支付的费用为27520元，所以$x$必定大于25。
当$x ＞ 25$时，每增加1人，人均旅游费用降低20元，因此人均费用表达式为$1000 - 20(x - 25)$。
于是可以列出方程：
$x[1000 - 20(x - 25)] = 27520$
展开并整理得：
$x^2 - 75x + 1376 = 0$
接下来，我们使用一元二次方程的求根公式来求解这个方程。
求根公式为：
$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
其中，$a = 1, b = -75, c = 1376$。
代入求根公式，得到：
$x = \frac{75 \pm \sqrt{(-75)^2 - 4 × 1 × 1376}}{2 × 1}$
$x = \frac{75 \pm \sqrt{5625 - 5504}}{2}$
$x = \frac{75 \pm \sqrt{121}}{2}$
$x = \frac{75 \pm 11}{2}$
解得：
$x_1 = \frac{86}{2} = 43, \quad x_2 = \frac{64}{2} = 32$
我们需要检验这两个解是否符合题目中人均费用不得低于700元的条件。
当$x = 43$时，
人均费用为$1000 - 20(43 - 25) = 1000 - 360 = 640$元，
小于700元，所以$x = 43$不符合题意，应舍去。
当$x = 32$时，
人均费用为$1000 - 20(32 - 25) = 1000 - 140 = 860$元，
大于700元，符合题意。
因此，单位这次共有32名员工去A风景区旅游。
【答案】：
单位这次共有 32 名员工去 A 风景区旅游。