《2025年创新课时作业本九年级数学上册苏州专版》

7. 如图,在边长为4的正方形$ABCD$中,以点$B$为圆心,$BA的长为半径作弧AC$,$F为弧AC$上一动点,过点$F作\odot B的切线交AD于点P$,交$DC于点Q$.
求证：$\triangle DPQ的周长等于正方形ABCD$周长的一半.

答案： 证明：
∵四边形ABCD是正方形，边长为4，
∴BA=BC=4，∠A=∠C=90°，AD=DC=4，正方形周长为16，其一半为8。
∵PQ切⊙B于F，
∴PF=PA，QF=QC（切线长定理）。
△DPQ的周长=PD+DQ+PQ
=PD+DQ+(PF+QF)
=PD+DQ+PA+QC（
∵PF=PA，QF=QC）
=(PD+PA)+(DQ+QC)
=AD+DC
=4+4=8。
∵正方形ABCD周长的一半为8，
∴△DPQ的周长等于正方形ABCD周长的一半。

8. 如图,过$\odot O外一点P引\odot O的两条切线PA$、$PB$,切点分别是$A$、$B$,$OP交\odot O于点C$,$D是优弧AB上不与点A$、$B$重合的一个动点,连接$AD$、$CD$,若$∠APB = 76^{\circ}$,则$∠ADC$的度数为( A)
A.$26^{\circ}$
B.$20^{\circ}$
C.$16^{\circ}$
D.$30^{\circ}$

答案： 【解析】：本题可根据切线的性质求出$\angle AOP$和$\angle BOP$的度数，再利用圆周角定理求出$\angle ADC$的度数。
步骤一：根据切线的性质求出$\angle AOP$和$\angle BOP$的度数
已知$PA$、$PB$是$\odot O$的切线，切点分别是$A$、$B$，根据切线的性质：圆的切线垂直于经过切点的半径，可得$OA\perp PA$，$OB\perp PB$，即$\angle OAP = \angle OBP = 90^{\circ}$。
在四边形$OAPB$中，$\angle OAP = \angle OBP = 90^{\circ}$，$\angle APB = 76^{\circ}$，根据四边形内角和为$360^{\circ}$，可得$\angle AOB + \angle OAP + \angle APB + \angle OBP = 360^{\circ}$，则$\angle AOB = 360^{\circ} - 90^{\circ} - 90^{\circ} - 76^{\circ} = 104^{\circ}$。
因为$OA = OB$（圆的半径相等），$OP$平分$\angle AOB$（等腰三角形三线合一），所以$\angle AOC = \angle BOC = \frac{1}{2}\angle AOB = \frac{1}{2}×104^{\circ} = 52^{\circ}$。
步骤二：根据圆周角定理求出$\angle ADC$的度数
根据圆周角定理：同弧或等弧所对的圆周角等于它所对圆心角的一半，因为$\overset{\frown}{AC}$所对的圆心角是$\angle AOC$，圆周角是$\angle ADC$，所以$\angle ADC = \frac{1}{2}\angle AOC = \frac{1}{2}×52^{\circ} = 26^{\circ}$。
【答案】：A

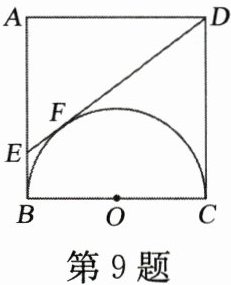
9. 如图,以边长为4的正方形$ABCD的边BC为直径作半圆O$,过点$D作直线切半圆于点F$,交$AB于点E$,则$\triangle ADE$的面积是____.

6

答案： 解：
∵ 四边形 $ABCD$ 是正方形，边长为4，
∴ $AB=BC=CD=AD=4$，$\angle A=\angle B=\angle C=90^\circ$。
∵ 半圆 $O$ 以 $BC$ 为直径，
∴ $OB=OC=2$，圆心 $O$ 为 $BC$ 中点。
设 $AE=x$，则 $BE=AB-AE=4-x$。
∵ $ED$ 切半圆 $O$ 于点 $F$，
∴ $EF=BE=4-x$（切线长定理，$EB$、$EF$ 均为半圆切线），
同理 $DF=DC=4$（$DC$、$DF$ 均为半圆切线）。
∴ $ED=EF+FD=(4-x)+4=8-x$。
在 $Rt\triangle AED$ 中，$AE=x$，$AD=4$，$ED=8-x$，
由勾股定理得：$AE^2+AD^2=ED^2$，
即 $x^2+4^2=(8-x)^2$，
解得 $x=3$。
∴ $S_{\triangle ADE}=\frac{1}{2}× AE× AD=\frac{1}{2}×3×4=6$。
答案：6

(1)如图②,试探究圆的外切四边形$ABCD的两组对边AD$、$BC与AB$、$CD$之间的数量关系,猜想：$AD + BC$=$AB + CD$；(选填“$＞$”“$＜$”或“$=$”)
(2)利用图②证明你的猜想(写出已知,求证和证明过程).
已知：四边形ABCD是⊙O的外切四边形，⊙O与四边形ABCD的边AB、BC、CD、DA分别相切于点G、F、E、H。
求证：AD + BC = AB + CD。
证明：∵⊙O与AB、BC、CD、DA分别相切于点G、F、E、H，
∴AG = AH，BG = BF，CF = CE，DE = DH。
∵AD = AH + DH，BC = BF + CF，AB = AG + BG，CD = CE + DE，
∴AD + BC = (AH + DH) + (BF + CF) = (AG + DE) + (BG + CE)，
AB + CD = (AG + BG) + (CE + DE) = AG + BG + CE + DE，
∴AD + BC = AB + CD。

答案：
(1)=
(2)已知：四边形ABCD是⊙O的外切四边形，⊙O与四边形ABCD的边AB、BC、CD、DA分别相切于点G、F、E、H。
求证：AD + BC = AB + CD。
证明：
∵⊙O与AB、BC、CD、DA分别相切于点G、F、E、H，
∴AG = AH，BG = BF，CF = CE，DE = DH。
∵AD = AH + DH，BC = BF + CF，AB = AG + BG，CD = CE + DE，
∴AD + BC = (AH + DH) + (BF + CF) = (AG + DE) + (BG + CE)，
AB + CD = (AG + BG) + (CE + DE) = AG + BG + CE + DE，
∴AD + BC = AB + CD。

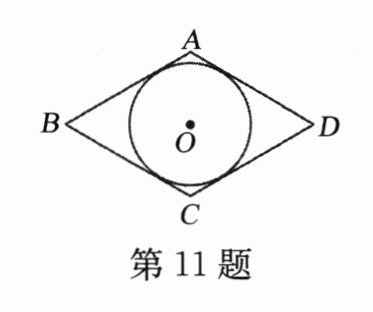
11. 如图,菱形$ABCD$,$∠B = 60^{\circ}$,$AB = 4$,$\odot O内切于菱形ABCD$,则$\odot O$的半径为____.

√3

答案： 解：连接AC，BD交于点O，过O作OE⊥AB于E。
∵菱形ABCD，∠B=60°，AB=4，
∴AB=BC=4，AC⊥BD，∠ABO=30°，
∴△ABC为等边三角形，AC=AB=4，
∴AO=2，
在Rt△ABO中，BO=√(AB²-AO²)=√(4²-2²)=2√3，
∴S菱形ABCD=AC·BD/2=4×4√3/2=8√3，
∵S菱形ABCD=AB·2OE，
∴8√3=4×2OE，
解得OE=√3，即⊙O的半径为√3。
√3

12. 如图,在$Rt\triangle ABC$中,$∠C = 90^{\circ}$,$AE平分∠BAC交BC于点E$,点$D在AB$上,$DE⊥AE$.$\odot O是Rt\triangle ADE$的外接圆,交$AC于点F$.
(1)求证：$BC是\odot O$的切线；
(2)若$\odot O$的半径为5,$AC = 8$,求$S_{\triangle ADE}$.

答案：
(1)证明：连接OE。
∵DE⊥AE，
∴∠AED=90°，
∴AD是⊙O的直径，点O是AD中点。
∵OA=OE，
∴∠OAE=∠OEA。
∵AE平分∠BAC，
∴∠OAE=∠CAE，
∴∠OEA=∠CAE，
∴OE//AC。
∵∠C=90°，
∴∠OEB=∠C=90°，即OE⊥BC。
∵OE是⊙O半径，
∴BC是⊙O的切线。
(2)解：
∵⊙O半径为5，
∴AD=10，OE=OA=OD=5。
由
(1)知OE//AC，
∴△BOE∽△BAC，
∴$\frac{OE}{AC}=\frac{BO}{BA}$。设BO=x，则BA=x+5。
∵AC=8，
∴$\frac{5}{8}=\frac{x}{x+5}$，解得x=$\frac{25}{3}$，
∴BA=$\frac{25}{3}+5=\frac{40}{3}$。
在Rt△ABC中，BC=$\sqrt{AB^2-AC^2}=\sqrt{(\frac{40}{3})^2-8^2}=\frac{32}{3}$。
∵△BOE∽△BAC，相似比$\frac{5}{8}$，
∴$\frac{BE}{BC}=\frac{5}{8}$，BE=$\frac{5}{8}×\frac{32}{3}=\frac{20}{3}$，
∴CE=BC-BE=$\frac{32}{3}-\frac{20}{3}=4$。
在Rt△ACE中，AE=$\sqrt{AC^2+CE^2}=\sqrt{8^2+4^2}=4\sqrt{5}$。
在Rt△ADE中，DE=$\sqrt{AD^2-AE^2}=\sqrt{10^2-(4\sqrt{5})^2}=2\sqrt{5}$，
∴$S_{\triangle ADE}=\frac{1}{2}×AE×DE=\frac{1}{2}×4\sqrt{5}×2\sqrt{5}=20$。
答案：
(1)见证明过程；
(2)20。