《2025年创新课时作业本九年级数学上册苏州专版》

8. 如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为 (A)
A.4
B.2
C.$\sqrt{3}$
D.$\sqrt{2}$

答案： 解：设⊙O的半径为r。
对于内接正△DEF：连接OD、OE，∠DOE=120°。过O作OH⊥DE于H，OH=r·cos60°=r/2，DH=r·sin60°=√3r/2，DE=2DH=√3r。S_△DEF=3×(1/2)×DE×OH=3×(1/2)×√3r×(r/2)=3√3r²/4。
对于外切正△ABC：连接OB、OC，∠BOC=120°。设BC与⊙O切于点M，OM=r，∠OBM=30°，BM=r/tan30°=√3r，BC=2BM=2√3r。S_△ABC=3×(1/2)×BC×r=3×(1/2)×2√3r×r=3√3r²。
面积比S_△ABC:S_△DEF=3√3r²:(3√3r²/4)=4。
答案：A

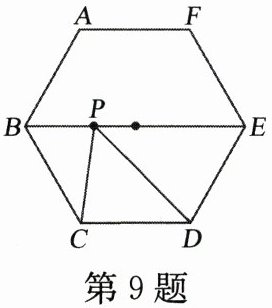
9. 如图,在边长为2的正六边形ABCDEF中,P是其对角线BE上一动点,连接PC、PD,则△PCD的周长的最小值是____.

6

答案： 解：在正六边形ABCDEF中，CD=2。作点C关于BE的对称点A，连接AD交BE于点P，此时PC+PD最小。
∵正六边形边长为2，
∴AD为经过中心的对角线，AD=4。
△PCD周长最小值=PC+PD+CD=AD+CD=4+2=6。
6

10. 如图,已知正方形ABCD的边心距$OE= \sqrt{2}cm$,求这个正方形外接圆⊙O的面积.

答案： 解：连接OC、OD。
∵四边形ABCD是正方形，
∴∠COD=360°/4=90°。
∵OE是边心距，
∴OE⊥CD，CE=DE，OE平分∠COD，
∴∠COE=∠DOE=45°。
在Rt△OEC中，sin∠COE=CE/OC，cos∠COE=OE/OC。
∵∠COE=45°，OE=√2cm，
∴OC=OE/cos45°=√2/(√2/2)=2cm。
∴⊙O的面积S=π·OC²=π×2²=4π cm²。
答：这个正方形外接圆⊙O的面积为4π cm²。

11. 如图,正六边形ABCDEF内接于⊙O,点P在$\overset{\frown}{AB}$上,Q是$\overset{\frown}{DE}$的中点,则∠CPQ的度数为 (B)
A.$30^{\circ}$
B.$45^{\circ}$
C.$36^{\circ}$
D.$60^{\circ}$

答案： 解：连接OC、OD、OQ、OP。
∵正六边形ABCDEF内接于⊙O，
∴∠COD=∠DOE=60°，OC=OD=OE。
∵Q是$\overset{\frown}{DE}$的中点，
∴∠DOQ=∠QOE=30°，∠COQ=∠COD+∠DOQ=60°+30°=90°。
∵点P在$\overset{\frown}{AB}$上，
∴∠COP=∠AOC+∠AOP=60°+∠AOP（∠AOC=60°）。
又
∵∠AOB=60°，点P在$\overset{\frown}{AB}$上，设∠AOP=α（0°＜α＜60°），则∠POQ=∠COQ - ∠COP=90° - (60°+α)=30° - α。
在△OCQ中，OC=OQ，∠COQ=90°，
∴∠OCQ=∠OQC=45°。
在△OPC中，OC=OP，∠COP=60°+α，
∴∠OCP=∠OPC=(180° - (60°+α))/2=60° - α/2。
在△OPQ中，OP=OQ，∠POQ=30° - α，
∴∠OPQ=∠OQP=(180° - (30° - α))/2=75° + α/2。
∵∠OPC + ∠OPQ + ∠CPQ=180°（平角定义），
∴(60° - α/2)+(75° + α/2)+∠CPQ=180°，
解得∠CPQ=45°。
答案：B

12. 阅读与思考.
请阅读下列材料,并完成相应的任务:
克罗狄斯·托勒密(约90年—168年),是希腊数学家,天文学家,地理学家和占星家.在数学方面,他还论证了四边形的特性,即有名的托勒密定理,托勒密定理的内容如下:圆的内接四边形的两条对角线的乘积等于两组对边乘积的和.即:如图①,若四边形ABCD内接于⊙O,则有____.
任务:(1) 材料中横线部分应填写的内容为$AC \cdot BD = AB \cdot CD + AD \cdot BC$;
(2) 如图②,正五边形ABCDE内接于⊙O,AB= 2,求对角线BD的长.

解：连接AD。
∵五边形ABCDE是正五边形，
∴$AB = BC = CD = DE = EA = 2$，$\angle BAD = \angle ADE = \angle BCD$，
∴$\triangle ABD \sim \triangle DBC$，
∴$\frac{BD}{BC} = \frac{AB}{BD - AB}$。
设$BD = x$，则$\frac{x}{2} = \frac{2}{x - 2}$，
整理得$x^2 - 2x - 4 = 0$，
解得$x = 1 + \sqrt{5}$（负值舍去）。
∴对角线BD的长为$1 + \sqrt{5}$。

答案：
(1) $AC \cdot BD = AB \cdot CD + AD \cdot BC$
(2) 解：连接AD。
∵五边形ABCDE是正五边形，
∴$AB = BC = CD = DE = EA = 2$，$\angle BAD = \angle ADE = \angle BCD$，
∴$\triangle ABD \sim \triangle DBC$，
∴$\frac{BD}{BC} = \frac{AB}{BD - AB}$。
设$BD = x$，则$\frac{x}{2} = \frac{2}{x - 2}$，
整理得$x^2 - 2x - 4 = 0$，
解得$x = 1 + \sqrt{5}$（负值舍去）。
∴对角线BD的长为$1 + \sqrt{5}$。