《2025年创新课时作业本九年级数学上册苏州专版》

8. 如图,某玩具品牌的标志由半径为$1cm$的三个等圆构成,且三个等圆$\odot O_{1}$、$\odot O_{2}$、$\odot O_{3}$相互经过彼此的圆心,则图中三个阴影部分的面积之和为 (C)
A.$\frac{1}{4}\pi cm^{2}$
B.$\frac{1}{3}\pi cm^{2}$
C.$\frac{1}{2}\pi cm^{2}$
D.$\pi cm^{2}$

答案： 解：连接$O_1O_2$、$O_2O_3$、$O_3O_1$。
因为三个等圆半径均为$1cm$，且相互经过彼此圆心，所以$O_1O_2=O_2O_3=O_3O_1=1cm$，$\triangle O_1O_2O_3$是等边三角形，每个内角为$60^\circ$，即$\frac{\pi}{3}$弧度。
每个阴影部分为扇形，其半径为$1cm$，圆心角为$60^\circ$。
一个扇形面积$S_1=\frac{60^\circ}{360^\circ}×\pi×1^2=\frac{1}{6}\pi cm^2$。
三个阴影部分面积之和$S=3×\frac{1}{6}\pi=\frac{1}{2}\pi cm^2$。
答案：C

9. 在如图所示的网格中,每个小正方形的边长均为$1cm$,则经过$A$、$B$、$C$三点的弧长是$\frac{5\pi}{4}$$cm$(结果保留$\pi$).

答案： 【解析】：本题考查了弧长公式$l=\frac{n\pi r}{180}$（其中$l$为弧长，$n$为圆心角度数，$r$为半径），要求经过$A$、$B$、$C$三点的弧长，需要先确定该弧所在圆的半径和圆心角的度数。
通过网格可发现$\triangle ABC$是直角三角形，$\angle ABC = 90^{\circ}$，根据圆周角定理的推论“$90^{\circ}$的圆周角所对的弦是直径”，可知$AC$是该弧所在圆的直径。
利用勾股定理求出$AC$的长度，进而得到半径，再根据圆周角定理求出圆心角的度数，最后代入弧长公式计算弧长。
1. 求$AC$的长度：
在网格中，根据勾股定理$a^2 + b^2 = c^2$（其中$a$、$b$为直角边，$c$为斜边），$A$点坐标可看作$(0,4)$，$C$点坐标可看作$(3,0)$，则$AC=\sqrt{4^{2}+3^{2}}=\sqrt{16 + 9}=\sqrt{25}=5（cm）$。
所以圆的半径$r = \frac{5}{2}cm$。
2. 求圆心角的度数：
因为$\angle ABC = 90^{\circ}$，根据圆周角定理的推论可知，$AC$所对的圆心角$n = 180^{\circ}×\frac{90^{\circ}}{180^{\circ}} = 90^{\circ}$（同弧所对的圆心角是圆周角的$2$倍）。
3. 计算弧长：
将$n = 90^{\circ}$，$r = \frac{5}{2}cm$代入弧长公式$l=\frac{n\pi r}{180}$，可得：
$l=\frac{90\pi×\frac{5}{2}}{180}=\frac{5\pi}{4}（cm）$。
【答案】：$\frac{5\pi}{4}$。

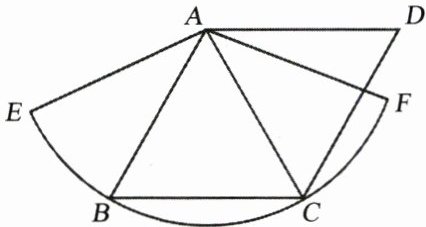
10. 如图,已知菱形$ABCD的边长为1.5cm$,$B$、$C两点在扇形AEF的\overset{\frown}{EF}$上,求$\overset{\frown}{BC}的长度及扇形ABC$的面积.

答案： 【解析】：
本题可先根据菱形的性质得出$\triangle ABC$是等边三角形，进而求出圆心角的度数，再结合弧长公式和扇形面积公式求解。
分析题目条件：
菱形$ABCD$的边长为$1.5cm$，即$AB = BC = 1.5cm$。
$B$、$C$两点在扇形$AEF$的$\overset{\frown}{EF}$上，说明$AB$、$AC$是扇形的半径，且$AB = AC = 1.5cm$。
根据上述条件可知$\triangle ABC$的三条边都相等，所以$\triangle ABC$是等边三角形。
求出圆心角$\angle BAC$的度数：
因为$\triangle ABC$是等边三角形，根据等边三角形的性质，其三个内角都为$60^{\circ}$，所以$\angle BAC = 60^{\circ}$。
计算$\overset{\frown}{BC}$的长度：
根据弧长公式$l=\frac{n\pi r}{180}$（其中$l$为弧长，$n$为圆心角度数，$r$为半径）。
已知$n = 60^{\circ}$，$r = AB = 1.5cm$，将其代入公式可得：
$l=\frac{60\pi×1.5}{180}=\frac{\pi}{2}(cm)$。
计算扇形$ABC$的面积：
根据扇形面积公式$S=\frac{n\pi r^{2}}{360}$（其中$S$为扇形面积，$n$为圆心角度数，$r$为半径）。
已知$n = 60^{\circ}$，$r = 1.5cm$，将其代入公式可得：
$S=\frac{60\pi×1.5^{2}}{360}=\frac{3\pi}{8}(cm^{2})$。
【答案】：
$\overset{\frown}{BC}$的长度为$\frac{\pi}{2}cm$，扇形$ABC$的面积为$\frac{3\pi}{8}cm^{2}$。

11. 如图,正方形$ABCD的边长为3$,以点$A$为圆心,$AB$的长为半径画弧,连接$AC$,以点$A$为圆心,$AC$的长为半径画弧,交$AD的延长线于点E$,则图中阴影部分的面积是____.


$\frac{9}{4}\pi -\frac{9}{2}$

答案： 解：
∵正方形ABCD边长为3，
∴AB=AD=3，∠BAD=90°，
AC=√(AB²+BC²)=√(3²+3²)=3√2。
S阴影=S扇形ACE - S扇形ACB - S△ACD。
S扇形ACE= (90°/360°)π(AC)²= (1/4)π(3√2)²= (1/4)π×18= (9/2)π。
S扇形ACB= (90°/360°)π(AB)²= (1/4)π×3²= (9/4)π。
S△ACD= (1/2)×AD×CD= (1/2)×3×3= 9/2。
∴S阴影= (9/2)π - (9/4)π - 9/2= (9/4)π - 9/2。
答案：(9/4)π - 9/2。

12. 如图,有一长为$4cm$,宽为$3cm$的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上的顶点$A的位置变化为A\rightarrow A_{1}\rightarrow A_{2}$,其中第二次翻滚被桌面上一小木块挡住,使木板边沿$A_{2}C与桌面成30^{\circ}$角,则点$A翻滚到A_{2}$位置时,求一共走过的路径长.

答案：

解：
∵长方形长为 4 cm，宽为 3 cm，

∴AB = 5 cm，第一次是以点 B 为旋转中心，BA 长 5 cm 为半径旋转 90°，此次点 A 走过的路径是$\frac{90\pi×5}{180}=\frac{5}{2}\pi$(cm)，第二次是以点 C 为旋转中心，4 cm 为半径旋转 60°，此次走过的路径是$\frac{60\pi×4}{180}=\frac{4}{3}\pi$(cm)，

∴点 A 两次共走过的路径是$\frac{5}{2}\pi+\frac{4}{3}\pi=\frac{23}{6}\pi$(cm)。