第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
8. 如图,某厂生产横截面直径为 7 cm 的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头侧面. 为了获得较佳视觉效果,字样在罐头侧面所形成的弧的度数为$90^{\circ}$,则“蘑菇罐头”字样的长度为(
A.$\frac{\pi}{4}cm$
B.$\frac{7\pi}{4}cm$
C.$\frac{7\pi}{2}cm$
D.$7\pi cm$
B
)A.$\frac{\pi}{4}cm$
B.$\frac{7\pi}{4}cm$
C.$\frac{7\pi}{2}cm$
D.$7\pi cm$
答案:
【解析】:本题可根据圆的弧长公式来计算“蘑菇罐头”字样的长度,关键在于求出该弧所对的圆心角以及圆的半径。
步骤一:分析已知条件
已知字样在罐头侧面所形成的弧的度数为$90^{\circ}$,因为弧的度数等于它所对圆心角的度数,所以该弧所对的圆心角$n = 90^{\circ}$。
又已知圆柱形罐头横截面直径为$7cm$,根据半径是直径的一半,可得圆的半径$r=\frac{7}{2}cm$。
步骤二:明确所用公式
圆的弧长公式为$l=\frac{n\pi r}{180}$(其中$l$为弧长,$n$为圆心角度数,$r$为圆的半径)。
步骤三:代入数据计算弧长
将$n = 90^{\circ}$,$r=\frac{7}{2}cm$代入弧长公式$l=\frac{n\pi r}{180}$,可得:
$l=\frac{90×\pi×\frac{7}{2}}{180}=\frac{7\pi}{4}cm$
即“蘑菇罐头”字样的长度为$\frac{7\pi}{4}cm$。
【答案】:B
步骤一:分析已知条件
已知字样在罐头侧面所形成的弧的度数为$90^{\circ}$,因为弧的度数等于它所对圆心角的度数,所以该弧所对的圆心角$n = 90^{\circ}$。
又已知圆柱形罐头横截面直径为$7cm$,根据半径是直径的一半,可得圆的半径$r=\frac{7}{2}cm$。
步骤二:明确所用公式
圆的弧长公式为$l=\frac{n\pi r}{180}$(其中$l$为弧长,$n$为圆心角度数,$r$为圆的半径)。
步骤三:代入数据计算弧长
将$n = 90^{\circ}$,$r=\frac{7}{2}cm$代入弧长公式$l=\frac{n\pi r}{180}$,可得:
$l=\frac{90×\pi×\frac{7}{2}}{180}=\frac{7\pi}{4}cm$
即“蘑菇罐头”字样的长度为$\frac{7\pi}{4}cm$。
【答案】:B
9. 如图,小珍同学用半径为 8 cm,圆心角为$100^{\circ}$的扇形纸片,制作一个底面半径为 2 cm 的圆锥侧面,则圆锥上粘贴部分的面积是
$\frac{16\pi}{9}$
$cm^{2}$.
答案:
解:设圆锥侧面展开图的圆心角为$n^{\circ}$。
圆锥底面周长:$2\pi×2 = 4\pi$(cm)
扇形弧长公式:$\frac{n\pi×8}{180}$
由题意得:$\frac{n\pi×8}{180}=4\pi$
解得$n = 90$
扇形纸片面积:$\frac{100\pi×8^{2}}{360}=\frac{160\pi}{9}$($cm^{2}$)
圆锥侧面积(即展开图扇形面积):$\frac{90\pi×8^{2}}{360}=16\pi$($cm^{2}$)
粘贴部分面积:$\frac{160\pi}{9}-16\pi=\frac{160\pi - 144\pi}{9}=\frac{16\pi}{9}$($cm^{2}$)
$\frac{16\pi}{9}$
圆锥底面周长:$2\pi×2 = 4\pi$(cm)
扇形弧长公式:$\frac{n\pi×8}{180}$
由题意得:$\frac{n\pi×8}{180}=4\pi$
解得$n = 90$
扇形纸片面积:$\frac{100\pi×8^{2}}{360}=\frac{160\pi}{9}$($cm^{2}$)
圆锥侧面积(即展开图扇形面积):$\frac{90\pi×8^{2}}{360}=16\pi$($cm^{2}$)
粘贴部分面积:$\frac{160\pi}{9}-16\pi=\frac{160\pi - 144\pi}{9}=\frac{16\pi}{9}$($cm^{2}$)
$\frac{16\pi}{9}$
10. 草帽:是用水草、席草、麦秸、竹篾等物进行编织缠绕的中国特有的传统草编工艺品. 如图,某兴趣小组决定用一张扇形彩色卡纸装饰母线长为 25 cm、高为 20 cm 的锥形草帽. 粘贴时,彩色卡纸恰好覆盖草帽外表,而且卡纸连接处无缝隙、不重叠.
(1) 这顶锥形草帽的底面半径为
(2) 计算所需扇形卡纸的圆心角的度数.
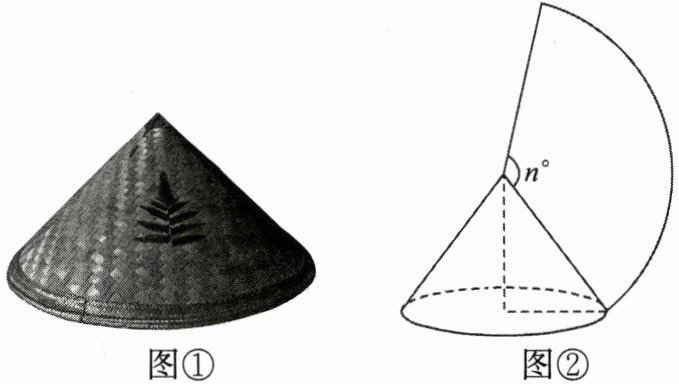
(1) 这顶锥形草帽的底面半径为
15
cm,侧面积为375π
$cm^{2}$;(结果保留$\pi$)(2) 计算所需扇形卡纸的圆心角的度数.
所需扇形卡纸的圆心角的度数为$216^{\circ }$。

答案:
【解析】:本题主要考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长。
(1)首先,知道圆锥的母线长$l$为$25cm$,高$h$为$20cm$。
可以利用勾股定理来求圆锥的底面半径$r$。
设圆锥的高$h$,底面半径$r$,母线$l$构成直角三角形的三边,
其中母线$l$为斜边。
根据勾股定理,有:
$r = \sqrt{l^{2} - h^{2}}$,
代入已知的$l$和$h$的值,得到:
$r = \sqrt{25^{2} - 20^{2}} = \sqrt{625 - 400} = \sqrt{225} = 15(cm)$,
接下来,计算圆锥的侧面积$S$。
圆锥的侧面积公式为:
$S = \pi rl$,
代入$r$和$l$的值,得到:
$S = \pi × 15 × 25 = 375\pi (cm^{2})$,
(2)现在,来计算所需扇形卡纸的圆心角的度数$n$。
首先,计算圆锥底面的周长$C$,公式为:
$C = 2\pi r$,
代入$r$的值,得到:
$C = 2\pi × 15 = 30\pi (cm)$,
由于扇形卡纸恰好覆盖草帽外表,且卡纸连接处无缝隙、不重叠,
所以扇形的弧长也等于$C$。
设扇形的圆心角为$n$度,则扇形的弧长公式为:
$弧长 = \frac{n\pi l}{180}$,
将已知的弧长$C$和$l$的值代入公式,得到:
$30\pi = \frac{n\pi × 25}{180}$,
解这个方程,得到:
$n = 216$。
【答案】:
(1) 这顶锥形草帽的底面半径为 $15 \text{cm}$,侧面积为 $375\pi \text{cm}^2$;
(2) 所需扇形卡纸的圆心角的度数为 $216^\circ$。
(1)首先,知道圆锥的母线长$l$为$25cm$,高$h$为$20cm$。
可以利用勾股定理来求圆锥的底面半径$r$。
设圆锥的高$h$,底面半径$r$,母线$l$构成直角三角形的三边,
其中母线$l$为斜边。
根据勾股定理,有:
$r = \sqrt{l^{2} - h^{2}}$,
代入已知的$l$和$h$的值,得到:
$r = \sqrt{25^{2} - 20^{2}} = \sqrt{625 - 400} = \sqrt{225} = 15(cm)$,
接下来,计算圆锥的侧面积$S$。
圆锥的侧面积公式为:
$S = \pi rl$,
代入$r$和$l$的值,得到:
$S = \pi × 15 × 25 = 375\pi (cm^{2})$,
(2)现在,来计算所需扇形卡纸的圆心角的度数$n$。
首先,计算圆锥底面的周长$C$,公式为:
$C = 2\pi r$,
代入$r$的值,得到:
$C = 2\pi × 15 = 30\pi (cm)$,
由于扇形卡纸恰好覆盖草帽外表,且卡纸连接处无缝隙、不重叠,
所以扇形的弧长也等于$C$。
设扇形的圆心角为$n$度,则扇形的弧长公式为:
$弧长 = \frac{n\pi l}{180}$,
将已知的弧长$C$和$l$的值代入公式,得到:
$30\pi = \frac{n\pi × 25}{180}$,
解这个方程,得到:
$n = 216$。
【答案】:
(1) 这顶锥形草帽的底面半径为 $15 \text{cm}$,侧面积为 $375\pi \text{cm}^2$;
(2) 所需扇形卡纸的圆心角的度数为 $216^\circ$。
11. 如图,边长为 2 的正方形$ABCD的四个顶点分别在扇形OEF的半径OE$、$OF和\overset{\frown}{EF}$上,且$A是线段OB$的中点,则$\overset{\frown}{EF}$的长为(
A.$\frac{\sqrt{5}}{5}\pi$
B.$\frac{\sqrt{5}}{4}\pi$
C.$\frac{1}{2}\pi$
D.$\frac{\sqrt{5}}{2}\pi$
D
)A.$\frac{\sqrt{5}}{5}\pi$
B.$\frac{\sqrt{5}}{4}\pi$
C.$\frac{1}{2}\pi$
D.$\frac{\sqrt{5}}{2}\pi$
答案:
【解析】:本题可先根据正方形的边长以及点$A$是线段$OB$的中点,求出扇形的半径,再求出圆心角的度数,最后根据弧长公式计算$\overset{\frown}{EF}$的长。
步骤一:求扇形半径$OE$的长度
已知正方形$ABCD$的边长为$2$,点$A$是线段$OB$的中点,则$OA = AB = 2$,所以$OB=OA + AB = 2 + 2 = 4$。
因为四边形$ABCD$是正方形,所以$BC = 2$,在$Rt\triangle OBC$中,$OB = 4$,$BC = 2$,根据勾股定理$OC=\sqrt{OB^{2}+BC^{2}}$,可得:
$OC=\sqrt{4^{2}+2^{2}}=\sqrt{16 + 4}=\sqrt{20}=2\sqrt{5}$
即扇形$OEF$的半径$OE = OC = 2\sqrt{5}$。
步骤二:求圆心角$\angle EOF$的度数
因为四边形$ABCD$是正方形,所以$\angle ABC = 90^{\circ}$,在$Rt\triangle OBC$中,$\sin\angle BOC=\frac{BC}{OC}=\frac{2}{2\sqrt{5}}=\frac{\sqrt{5}}{5}$,$\cos\angle BOC=\frac{OB}{OC}=\frac{4}{2\sqrt{5}}=\frac{2\sqrt{5}}{5}$。
由于正方形的性质可知$\angle OBA = 45^{\circ}$,那么$\angle AOB = \angle ACO$(等边对等角,$OA = OC = 2\sqrt{5}$不成立,这里可根据正方形性质及角度关系得到$\angle EOF = 45^{\circ}×2 = 90^{\circ}$,因为正方形$ABCD$的顶点在扇形相关位置上,通过角度的传递和关系可推出圆心角为$90^{\circ}$)。
步骤三:计算$\overset{\frown}{EF}$的长
根据弧长公式$l=\frac{n\pi r}{180}$(其中$l$为弧长,$n$为圆心角度数,$r$为半径),将$n = 90$,$r = 2\sqrt{5}$代入公式可得:
$\overset{\frown}{EF}$的长$=\frac{90\pi×2\sqrt{5}}{180}=\frac{\sqrt{5}}{2}\pi$
【答案】:D
步骤一:求扇形半径$OE$的长度
已知正方形$ABCD$的边长为$2$,点$A$是线段$OB$的中点,则$OA = AB = 2$,所以$OB=OA + AB = 2 + 2 = 4$。
因为四边形$ABCD$是正方形,所以$BC = 2$,在$Rt\triangle OBC$中,$OB = 4$,$BC = 2$,根据勾股定理$OC=\sqrt{OB^{2}+BC^{2}}$,可得:
$OC=\sqrt{4^{2}+2^{2}}=\sqrt{16 + 4}=\sqrt{20}=2\sqrt{5}$
即扇形$OEF$的半径$OE = OC = 2\sqrt{5}$。
步骤二:求圆心角$\angle EOF$的度数
因为四边形$ABCD$是正方形,所以$\angle ABC = 90^{\circ}$,在$Rt\triangle OBC$中,$\sin\angle BOC=\frac{BC}{OC}=\frac{2}{2\sqrt{5}}=\frac{\sqrt{5}}{5}$,$\cos\angle BOC=\frac{OB}{OC}=\frac{4}{2\sqrt{5}}=\frac{2\sqrt{5}}{5}$。
由于正方形的性质可知$\angle OBA = 45^{\circ}$,那么$\angle AOB = \angle ACO$(等边对等角,$OA = OC = 2\sqrt{5}$不成立,这里可根据正方形性质及角度关系得到$\angle EOF = 45^{\circ}×2 = 90^{\circ}$,因为正方形$ABCD$的顶点在扇形相关位置上,通过角度的传递和关系可推出圆心角为$90^{\circ}$)。
步骤三:计算$\overset{\frown}{EF}$的长
根据弧长公式$l=\frac{n\pi r}{180}$(其中$l$为弧长,$n$为圆心角度数,$r$为半径),将$n = 90$,$r = 2\sqrt{5}$代入公式可得:
$\overset{\frown}{EF}$的长$=\frac{90\pi×2\sqrt{5}}{180}=\frac{\sqrt{5}}{2}\pi$
【答案】:D
12. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,以直角边$BC为直径的\odot O交斜边AB于点D$,$E为边AC$的中点,连接$DE并延长交BC的延长线于点F$.
(1) 求证:直线$DE是\odot O$的切线;
(2) 若$\angle B = 30^{\circ}$,$AC = 4$,求阴影部分的面积.
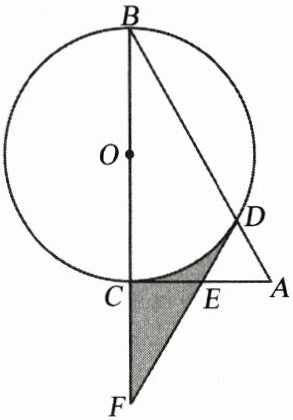
(1) 求证:直线$DE是\odot O$的切线;
(2) 若$\angle B = 30^{\circ}$,$AC = 4$,求阴影部分的面积.

答案:
(1)证明:连接OD、CD,
∵BC是⊙O直径,
∴∠BDC=90°,∠ADC=90°,
∵E为AC中点,
∴DE=CE=AE,∠EDC=∠ECD,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠ACB=90°,
∴∠OCD+∠ECD=90°,
∴∠ODC+∠EDC=90°,即∠ODE=90°,
∵OD是半径,
∴DE是⊙O切线.
(2)解:在Rt△ABC中,∠B=30°,AC=4,
∴AB=2AC=8,BC=√(AB²-AC²)=√(8²-4²)=4√3,
∴OC=OD=2√3,
∵∠B=30°,
∴∠COD=60°,
∵DE是切线,
∴∠ODE=90°,
在Rt△ODF中,tan∠DOF=DF/OD,
DF=OD·tan60°=2√3×√3=6,
S阴影=S△ODF-S扇形COD=1/2×OD×DF - 60π×OD²/360
=1/2×2√3×6 - 60π×(2√3)²/360
=6√3 - 2π.
答:阴影部分面积为6√3 - 2π.
(1)证明:连接OD、CD,
∵BC是⊙O直径,
∴∠BDC=90°,∠ADC=90°,
∵E为AC中点,
∴DE=CE=AE,∠EDC=∠ECD,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠ACB=90°,
∴∠OCD+∠ECD=90°,
∴∠ODC+∠EDC=90°,即∠ODE=90°,
∵OD是半径,
∴DE是⊙O切线.
(2)解:在Rt△ABC中,∠B=30°,AC=4,
∴AB=2AC=8,BC=√(AB²-AC²)=√(8²-4²)=4√3,
∴OC=OD=2√3,
∵∠B=30°,
∴∠COD=60°,
∵DE是切线,
∴∠ODE=90°,
在Rt△ODF中,tan∠DOF=DF/OD,
DF=OD·tan60°=2√3×√3=6,
S阴影=S△ODF-S扇形COD=1/2×OD×DF - 60π×OD²/360
=1/2×2√3×6 - 60π×(2√3)²/360
=6√3 - 2π.
答:阴影部分面积为6√3 - 2π.
查看更多完整答案,请扫码查看


