第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1. 圆是轴对称图形,
每条直径所在的直线
都是它的对称轴.
答案:
【解析】:
本题考查的是圆的对称性质。圆是一个特殊的几何图形,其上任取一点,关于圆心做对称点,该对称点也一定在圆上。这是因为圆上任意一点到圆心的距离都是相等的,即半径。因此,圆的任意直径都可以作为它的对称轴。
【答案】:
每条直径所在的直线。
本题考查的是圆的对称性质。圆是一个特殊的几何图形,其上任取一点,关于圆心做对称点,该对称点也一定在圆上。这是因为圆上任意一点到圆心的距离都是相等的,即半径。因此,圆的任意直径都可以作为它的对称轴。
【答案】:
每条直径所在的直线。
2. 垂径定理:垂直于弦的直径平分
这条弦
以及弦所对的两条弧
.
答案:
解:这条弦;两条弧
1. 如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,则下列结论中不一定成立的是 (
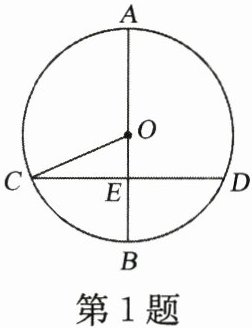
A.∠COE= ∠DOE
B.CE= DE
C.OA= DE
D.$\overset{\frown}{BD}= \overset{\frown}{BC}$
C
)
A.∠COE= ∠DOE
B.CE= DE
C.OA= DE
D.$\overset{\frown}{BD}= \overset{\frown}{BC}$
答案:
【解析】:
本题可根据圆的对称性以及垂径定理来逐一分析选项。
选项A:判断$\angle COE = \angle DOE$是否成立
因为$AB$是$\odot O$的直径,$CD\perp AB$于点$E$,根据圆的对称性可知,$AB$是圆$\odot O$的一条对称轴,$CD$关于$AB$对称,所以$\angle COE = \angle DOE$,该选项一定成立。
选项B:判断$CE = DE$是否成立
由垂径定理可知,垂直于弦的直径平分弦,因为$AB$是$\odot O$的直径,$CD\perp AB$于点$E$,所以$CE = DE$,该选项一定成立。
选项C:判断$OA = DE$是否成立
$OA$是圆$\odot O$的半径,$DE$是弦$CD$被直径$AB$所截得的一半,圆半径的长度与弦一半的长度并没有必然的相等关系,所以$OA$不一定等于$DE$,该选项不一定成立。
选项D:判断$\overset{\frown}{BD}= \overset{\frown}{BC}$是否成立
由于$AB$是$\odot O$的直径,$CD\perp AB$于点$E$,根据垂径定理可知,垂直于弦的直径平分弦且平分这条弦所对的两条弧,所以$\overset{\frown}{BD}= \overset{\frown}{BC}$,该选项一定成立。
综上,答案选C。
【答案】:C
本题可根据圆的对称性以及垂径定理来逐一分析选项。
选项A:判断$\angle COE = \angle DOE$是否成立
因为$AB$是$\odot O$的直径,$CD\perp AB$于点$E$,根据圆的对称性可知,$AB$是圆$\odot O$的一条对称轴,$CD$关于$AB$对称,所以$\angle COE = \angle DOE$,该选项一定成立。
选项B:判断$CE = DE$是否成立
由垂径定理可知,垂直于弦的直径平分弦,因为$AB$是$\odot O$的直径,$CD\perp AB$于点$E$,所以$CE = DE$,该选项一定成立。
选项C:判断$OA = DE$是否成立
$OA$是圆$\odot O$的半径,$DE$是弦$CD$被直径$AB$所截得的一半,圆半径的长度与弦一半的长度并没有必然的相等关系,所以$OA$不一定等于$DE$,该选项不一定成立。
选项D:判断$\overset{\frown}{BD}= \overset{\frown}{BC}$是否成立
由于$AB$是$\odot O$的直径,$CD\perp AB$于点$E$,根据垂径定理可知,垂直于弦的直径平分弦且平分这条弦所对的两条弧,所以$\overset{\frown}{BD}= \overset{\frown}{BC}$,该选项一定成立。
综上,答案选C。
【答案】:C
2. 如图,⊙O的弦AB垂直平分半径OC,则四边形OACB是 (
A.正方形
B.长方形
C.菱形
D.以上答案都不对
C
)A.正方形
B.长方形
C.菱形
D.以上答案都不对
答案:
【解析】:本题可根据圆的性质、线段垂直平分线的性质以及菱形的判定定理来求解。
步骤一:根据圆的性质得到相关线段关系
因为$OC$是圆$O$的半径,所以$OA = OB = OC$(圆的半径都相等)。
步骤二:根据线段垂直平分线的性质得到相关线段关系
已知弦$AB$垂直平分半径$OC$,设$AB$与$OC$的交点为$D$,则$OD = DC=\frac{1}{2}OC$,且$OA = AC$(线段垂直平分线上的点到这条线段两个端点的距离相等)。
同理可得$OB = BC$。
步骤三:结合上述结论得到四边形$OACB$的边的关系
由$OA = OB = OC$,$OA = AC$,$OB = BC$,可得$OA = AC = BC = OB$。
步骤四:根据菱形的判定定理得出结论
根据菱形的判定定理:四条边相等的四边形是菱形,由于四边形$OACB$的四条边$OA$、$AC$、$BC$、$OB$都相等,所以四边形$OACB$是菱形。
【答案】:C
步骤一:根据圆的性质得到相关线段关系
因为$OC$是圆$O$的半径,所以$OA = OB = OC$(圆的半径都相等)。
步骤二:根据线段垂直平分线的性质得到相关线段关系
已知弦$AB$垂直平分半径$OC$,设$AB$与$OC$的交点为$D$,则$OD = DC=\frac{1}{2}OC$,且$OA = AC$(线段垂直平分线上的点到这条线段两个端点的距离相等)。
同理可得$OB = BC$。
步骤三:结合上述结论得到四边形$OACB$的边的关系
由$OA = OB = OC$,$OA = AC$,$OB = BC$,可得$OA = AC = BC = OB$。
步骤四:根据菱形的判定定理得出结论
根据菱形的判定定理:四条边相等的四边形是菱形,由于四边形$OACB$的四条边$OA$、$AC$、$BC$、$OB$都相等,所以四边形$OACB$是菱形。
【答案】:C
3. 如图,OA、OB、OC都是⊙O的半径,AC、OB交于点D.若AD= CD= 8,OD= 6,则BD的长为 (
A.5
B.4
C.3
D.2
B
)A.5
B.4
C.3
D.2
答案:
解:设⊙O的半径为r,则OB=OA=OC=r,BD=OB-OD=r-6。
∵AD=CD=8,
∴D为AC中点。
∵OA=OC,
∴OD⊥AC(等腰三角形三线合一)。
在Rt△AOD中,OA²=AD²+OD²,即r²=8²+6²=64+36=100,
∴r=10。
∴BD=OB-OD=10-6=4。
答案:B
∵AD=CD=8,
∴D为AC中点。
∵OA=OC,
∴OD⊥AC(等腰三角形三线合一)。
在Rt△AOD中,OA²=AD²+OD²,即r²=8²+6²=64+36=100,
∴r=10。
∴BD=OB-OD=10-6=4。
答案:B
4. 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D,连接BC,若BC= 12,则OD=
6
.
答案:
【解析】:根据圆的性质,直径所对的圆周角为直角,所以$\angle C = 90^\circ$。
由于$OD \perp AC$,所以$OD$平行于$BC$(因为$OD$和$BC$都垂直于$AC$)。
由于$O$是$AB$的中点(因为$AB$是直径),所以$OD$是$\triangle ABC$的中位线。
根据中位线的性质,$OD = \frac{1}{2}BC$。
已知$BC = 12$,所以$OD = \frac{1}{2} × 12 = 6$。
【答案】:$OD = 6$。
由于$OD \perp AC$,所以$OD$平行于$BC$(因为$OD$和$BC$都垂直于$AC$)。
由于$O$是$AB$的中点(因为$AB$是直径),所以$OD$是$\triangle ABC$的中位线。
根据中位线的性质,$OD = \frac{1}{2}BC$。
已知$BC = 12$,所以$OD = \frac{1}{2} × 12 = 6$。
【答案】:$OD = 6$。
5. 如图,在⊙O中,直径AB⊥弦CD于点M,AM= 18,BM= 8,则CD的长为
24
.
答案:
【解析】:
本题主要考查了垂径定理以及勾股定理的应用。
首先,根据题目已知条件,直径 $AB = AM + BM = 18 + 8 = 26$,则半径 $OA = \frac{AB}{2} = 13$。
由于 $AB \perp CD$,根据垂径定理,我们知道 $CM = MD$,即 $CD$ 被 $AB$ 平分。
连接 $OC$,由于 $OC$ 是半径,所以 $OC = 13$,已知$OM=OA-AM=13-18=-5$(舍去)或$OM = AM - OA = 18 - 13 = 5$。
接下来,我们利用勾股定理在直角三角形 $OCM$ 中求解 $CM$ 的长度。
根据勾股定理,有:
$CM = \sqrt{OC^{2} - OM^{2}} = \sqrt{13^{2} - 5^{2}} = \sqrt{169 - 25} = \sqrt{144} = 12$,
最后,由于 $CD = 2CM$,所以 $CD = 2 × 12 = 24$。
【答案】:
24
本题主要考查了垂径定理以及勾股定理的应用。
首先,根据题目已知条件,直径 $AB = AM + BM = 18 + 8 = 26$,则半径 $OA = \frac{AB}{2} = 13$。
由于 $AB \perp CD$,根据垂径定理,我们知道 $CM = MD$,即 $CD$ 被 $AB$ 平分。
连接 $OC$,由于 $OC$ 是半径,所以 $OC = 13$,已知$OM=OA-AM=13-18=-5$(舍去)或$OM = AM - OA = 18 - 13 = 5$。
接下来,我们利用勾股定理在直角三角形 $OCM$ 中求解 $CM$ 的长度。
根据勾股定理,有:
$CM = \sqrt{OC^{2} - OM^{2}} = \sqrt{13^{2} - 5^{2}} = \sqrt{169 - 25} = \sqrt{144} = 12$,
最后,由于 $CD = 2CM$,所以 $CD = 2 × 12 = 24$。
【答案】:
24
6. 如图,在⊙O中,直径AB和弦CD相交于点E,已知AE= 1 cm,EB= 5 cm,且∠DEB= 60°,求CD的长.


答案:
【解析】:本题主要考查圆的性质、垂径定理以及三角函数的应用。
连接$OD$,因为$AB$是直径,$AE = 1cm$,$EB = 5cm$,所以圆的半径$OD=\frac{AE + EB}{2}=\frac{1 + 5}{2}=3cm$,则$OE=OA - AE=3 - 1 = 2cm$。
在$\triangle OED$中,已知$\angle DEB = 60^{\circ}$,过$O$作$OF\perp CD$于$F$,根据垂径定理可知$CD = 2DF$。
在$Rt\triangle OEF$中,$\angle DEB = 60^{\circ}$,$OE = 2cm$,则$OF = OE\sin60^{\circ}=2×\frac{\sqrt{3}}{2}=\sqrt{3}cm$。
在$Rt\triangle ODF$中,$OD = 3cm$,$OF=\sqrt{3}cm$,根据勾股定理$DF=\sqrt{OD^{2}-OF^{2}}=\sqrt{3^{2}-(\sqrt{3})^{2}}=\sqrt{9 - 3}=\sqrt{6}cm$。
所以$CD = 2DF = 2\sqrt{6}cm$。
【答案】:$CD = 2\sqrt{6}cm$
连接$OD$,因为$AB$是直径,$AE = 1cm$,$EB = 5cm$,所以圆的半径$OD=\frac{AE + EB}{2}=\frac{1 + 5}{2}=3cm$,则$OE=OA - AE=3 - 1 = 2cm$。
在$\triangle OED$中,已知$\angle DEB = 60^{\circ}$,过$O$作$OF\perp CD$于$F$,根据垂径定理可知$CD = 2DF$。
在$Rt\triangle OEF$中,$\angle DEB = 60^{\circ}$,$OE = 2cm$,则$OF = OE\sin60^{\circ}=2×\frac{\sqrt{3}}{2}=\sqrt{3}cm$。
在$Rt\triangle ODF$中,$OD = 3cm$,$OF=\sqrt{3}cm$,根据勾股定理$DF=\sqrt{OD^{2}-OF^{2}}=\sqrt{3^{2}-(\sqrt{3})^{2}}=\sqrt{9 - 3}=\sqrt{6}cm$。
所以$CD = 2DF = 2\sqrt{6}cm$。
【答案】:$CD = 2\sqrt{6}cm$
7. 唐代李皋发明了“桨轮船”,这种船是原始形态的轮船,是近代明轮航行模式之先导.如图,某桨轮船的轮子被水面截得的弦AB长为8米,轮子的半径AO为5米,求轮子的吃水深度CD.


答案:
【解析】:本题主要考查了圆的性质以及垂径定理的应用。
已知弦$AB$的长度为$8$米,轮子的半径$AO$为$5$米。
根据垂径定理,垂直于弦的直径平分弦,所以$AD = \frac{AB}{2} = 4(米)$。
接下来,利用勾股定理在直角三角形$AOD$中求解$OD$的长度。
根据勾股定理,有
$OD = \sqrt{OA^{2} - AD^{2}} = \sqrt{5^{2} - 4^{2}} = \sqrt{25 - 16} = \sqrt{9} = 3(米)$,
由于$OC$是轮子的半径,且$CD$是吃水深度,所以
$CD = OC - OD = 5米 - 3米 = 2米$。
【答案】:$2$米。
已知弦$AB$的长度为$8$米,轮子的半径$AO$为$5$米。
根据垂径定理,垂直于弦的直径平分弦,所以$AD = \frac{AB}{2} = 4(米)$。
接下来,利用勾股定理在直角三角形$AOD$中求解$OD$的长度。
根据勾股定理,有
$OD = \sqrt{OA^{2} - AD^{2}} = \sqrt{5^{2} - 4^{2}} = \sqrt{25 - 16} = \sqrt{9} = 3(米)$,
由于$OC$是轮子的半径,且$CD$是吃水深度,所以
$CD = OC - OD = 5米 - 3米 = 2米$。
【答案】:$2$米。
查看更多完整答案,请扫码查看


