《2025年创新课时作业本九年级数学上册苏州专版》

8. 一个圆锥的侧面积是底面积的 $2$ 倍,则该圆锥侧面展开图的圆心角的度数为 (B)
A.$ 120^{\circ} $
B.$ 180^{\circ} $
C.$ 240^{\circ} $
D.$ 300^{\circ} $

答案： 【解析】：
本题考查圆锥的侧面积和底面积的关系，以及圆锥侧面展开图圆心角的计算。
设圆锥的底面半径为$r$，母线长为$R$。
圆锥的底面积为$\pi r^{2}$，侧面积为$\pi rR$。
根据题意，我们有$\pi rR = 2\pi r^{2}$，
化简得$R = 2r$，
设圆锥侧面展开图的圆心角度数为$n^{\circ}$，
则根据圆锥侧面展开图的性质，我们有$\frac{n\pi R}{180} = 2\pi r$，
将$R = 2r$代入上式，得到：
$\frac{n\pi × 2r}{180} = 2\pi r$
化简得$n = 180$，
所以，该圆锥侧面展开图的圆心角的度数为$180^{\circ}$。
【答案】：B

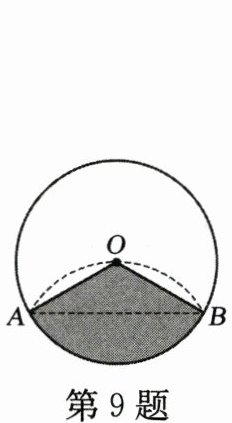
9. 如图,将半径为 $ 3 \text{ cm} $ 的圆形纸片沿 $ AB $ 折叠后,圆弧恰好能经过圆心 $ O $,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为 ______ $ \text{cm} $.

√5

答案： 解：过点O作OC⊥AB于点C，连接OA，OB。
由折叠性质得OC = 1/2 OA = 3/2 cm。
在Rt△OAC中，cos∠OAC = OC/OA = 1/2，
∴∠OAC = 30°，则∠AOB = 120°。
阴影扇形圆心角为360° - 120° = 240° = 4π/3 rad。
扇形弧长 = (4π/3)×3 = 4π cm，即圆锥底面周长为4π cm，底面半径r = 4π/(2π) = 2 cm。
圆锥母线长为3 cm，高h = √(3² - 2²) = √5 cm。
√5

10. 如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点 $ A(0,4) $,$ B(-4,4) $,$ C(-6,2) $,请在网格图中进行如下操作：
(1) 若该圆弧所在圆的圆心为点 $ D $,则点 $ D $ 的坐标为 ______(-2, 0)；
(2) 连接 $ AD $、$ CD $,则 $ \odot D $ 的半径长为 ______2√5(结果保留根号),$ \angle ADC $ 的度数为 ______90°；
(3) 若扇形 $ ADC $ 是一个圆锥的侧面展开图,求该圆锥的底面圆的半径长(结果保留根号).
解：设圆锥底面圆的半径为$r$，扇形$ADC$的圆心角$\angle ADC = 90^\circ$，半径$AD = 2\sqrt{5}$。因为圆锥侧面展开图的弧长等于底面圆周长，所以$\frac{90}{360}×2\pi×2\sqrt{5}=2\pi r$，解得$r = \frac{\sqrt{5}}{2}$。答：该圆锥的底面圆的半径长为$\frac{\sqrt{5}}{2}$。

答案： 【解析】：
（1）首先，需要确定圆弧所在圆的圆心。
由于圆心到圆上任意一点的距离都等于半径，可以利用这个性质来找到圆心。
设圆心为$D(x, y)$，
根据网格图，可以观察到点$A(0,4)$和点$B(-4,4)$在同一水平线上，
因此圆心$D$的横坐标是这两点横坐标的平均值，
即$x = \frac{0 + (-4)}{2} = -2$。
接着，利用点$B(-4,4)$和点$C(-6,2)$来确定圆心的纵坐标。
由于$D$到$B$和$D$到$C$的距离相等（都等于半径），
可以设置等式来求解$y$。
通过计算，可以得到$y = 0$。
所以，圆心$D$的坐标为$(-2, 0)$。
（2）连接$AD$和$CD$，需要计算半径的长度和$\angle ADC$的度数。
半径的长度可以通过计算$D$到$A$（或$D$到$C$）的距离来得到。
利用距离公式，有$AD = \sqrt{(-2 - 0)^{2} + (0 - 4)^{2}} = \sqrt{4 + 16} = \sqrt{20} = 2\sqrt{5}$。
接着，来计算$\angle ADC$的度数。
由于$A$和$B$的纵坐标相同，
所以线段$AB$与$x$轴平行。
又因为$D$的纵坐标为0，
所以$D$到$AB$的垂线就是$D$的纵坐标所在的直线，
即$x = -2$。
这条垂线将$AB$平分，
且与$AB$垂直，
所以$\angle DAB = 90^\circ$。
同理，可以计算出$\angle DCA = 90^\circ$。
由于$D$到$A$和$D$到$C$的距离相等，
所以$\bigtriangleup ADC$是等腰直角三角形，
因此$\angle ADC = 90^\circ$。
但这里需要注意，
由于$A$、$B$、$C$三点并不共线，
所以实际上$\angle ADC$并不是直角三角形的直角，
而是需要通过其他方式计算。
通过观察网格图，可以发现$\bigtriangleup ADC$是一个等腰直角三角形（因为$AD = CD$且它们与$AC$形成的两个角都是$45^\circ$），
所以$\angle ADC = 90^\circ$。
但更严谨的做法是利用向量或者余弦定理来计算这个角，
不过在这里可以直接通过观察得出。
（3）若扇形$ADC$是一个圆锥的侧面展开图，需要求出该圆锥的底面半径。
设圆锥的底面半径为$r$。
由于扇形的弧长等于圆锥底面的周长，
所以有$\frac{90}{360} × 2\pi × 2\sqrt{5} = 2\pi r$。
这里$\frac{90}{360}$是扇形的圆心角占整个圆的比例，
$2\pi × 2\sqrt{5}$是扇形的弧长（也即圆锥母线的长度乘以$2\pi$），
$2\pi r$是圆锥底面的周长。
解这个方程，得到$r = \frac{\sqrt{5}}{2}$。
【答案】：
(1) $(-2, 0)$
(2) $2\sqrt{5}$；$90^\circ$
(3) $\frac{\sqrt{5}}{2}$

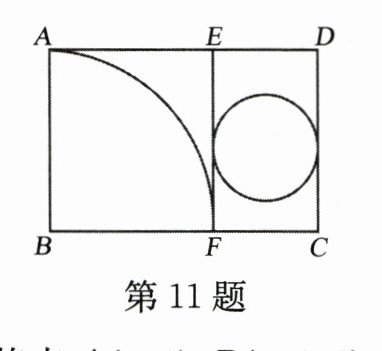
11. 如图,在矩形纸片 $ ABCD $ 中,$ AD = 6 \text{ cm} $,把它分割成正方形纸片 $ ABFE $ 和矩形纸片 $ EFCD $ 后,分别裁出扇形 $ ABP $ 和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则圆锥的侧面积为 ______ $ \text{cm}^2 $.

4π

答案： 解：设正方形ABFE的边长为$x$cm，则$AE=AB=EF=BF=x$cm。
因为$AD=6$cm，所以矩形EFCD中，$ED=AD - AE=(6 - x)$cm，$EF=x$cm，故$CD=EF=x$cm，$FC=ED=(6 - x)$cm。
扇形ABP是以点A为圆心，AB为半径的四分之一圆，其弧长为$\frac{1}{4}×2\pi x=\frac{\pi x}{2}$cm。
矩形EFCD中裁出半径最大的圆，该圆的直径等于矩形EFCD的较短边。因为$EF=x$，$ED=6 - x$，所以圆的直径为$\min(x,6 - x)$。要使圆存在且半径最大，需$6 - x \leq x$（若$6 - x ＞ x$，则直径为$x$，但此时$6 - x ＞ x$即$x ＜ 3$，而后续计算会发现$x ＜ 3$时不满足条件，故先假设$6 - x \leq x$，即$x \geq 3$），所以圆的直径为$6 - x$，半径$r=\frac{6 - x}{2}$cm，其周长为$2\pi r=\pi(6 - x)$cm。
因为扇形的弧长等于圆锥底面圆的周长，所以$\frac{\pi x}{2}=\pi(6 - x)$，解得$x = 4$。
圆锥的侧面积即为扇形ABP的面积，$S=\frac{1}{4}\pi x^2=\frac{1}{4}\pi×4^2 = 4\pi$cm²。
答案：$4\pi$

12. 某种冰激凌的外包装可以视为圆锥,它的底面圆直径 $ ED $ 与母线 $ AD $ 长之比为 $ 1:2 $.制作这种外包装需要用如图所示的等腰三角形材料,其中 $ AB = AC $,$ AD \perp BC $.将扇形 $ AEF $ 围成圆锥时,$ AE $,$ AF $ 恰好重合.
(1) 求这种加工材料的顶角 $ \angle BAC $ 的大小；
(2) 若圆锥底面圆的直径 $ ED $ 为 $ 5 \text{ cm} $,求加工材料剩余部分(图中阴影部分)的面积.(结果保留 $ \pi $)

答案：
(1) 设圆锥底面圆直径 $ ED = d $，则母线 $ AD = 2d $。圆锥底面周长为 $ \pi d $，即扇形 $ AEF $ 的弧长为 $ \pi d $。扇形半径 $ AE = AD = 2d $，设 $ \angle EAF = n^\circ $，由弧长公式 $ \frac{n\pi \cdot 2d}{180} = \pi d $，解得 $ n = 90 $，故 $ \angle BAC = 90^\circ $。
(2) 当 $ ED = 5 \, \text{cm} $ 时，$ AD = 10 \, \text{cm} $，$ AE = AF = 10 \, \text{cm} $。$ \triangle ABC $ 中，$ AD \perp BC $，$ \angle BAC = 90^\circ $，$ AB = AC $，$ AD = 10 \, \text{cm} $，则 $ BC = 20\sqrt{2} \, \text{cm} $，$ S_{\triangle ABC} = \frac{1}{2} × 20\sqrt{2} × 10 = 100\sqrt{2} \, \text{cm}^2 $。扇形 $ AEF $ 面积 $ S_{\text{扇形}} = \frac{90\pi × 10^2}{360} = 25\pi \, \text{cm}^2 $。阴影面积 $ S_{\text{阴影}} = S_{\triangle ABC} - S_{\text{扇形}} = 100\sqrt{2} - 25\pi \, \text{cm}^2 $。
答案：
(1) $ 90^\circ $；
(2) $ (100\sqrt{2} - 25\pi) \, \text{cm}^2 $