《2025年创新课时作业本九年级数学上册苏州专版》

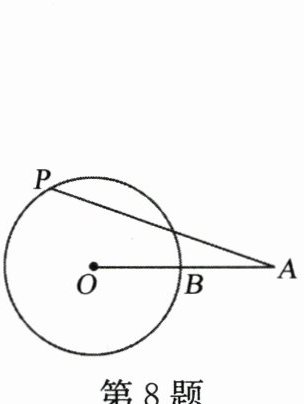
8. 如图,已知线段$OA交\odot O于点B$,且$OB= AB$,$P是\odot O$上的一个动点,那么$∠OAP$的最大值是 (D)

A.$90^{\circ}$
B.$60^{\circ}$
C.$45^{\circ}$
D.$30^{\circ}$

答案： 解：设 $ OB = r $，则 $ OA = OB + AB = 2r $。
当 $ AP $ 与 $ \odot O $ 相切时，$ \angle OAP $ 最大。
连接 $ OP $，则 $ OP \perp AP $，$ OP = r $。
在 $ Rt\triangle OPA $ 中，$ \sin \angle OAP = \frac{OP}{OA} = \frac{r}{2r} = \frac{1}{2} $。
$ \therefore \angle OAP = 30^{\circ} $。
答案：D

9. 如图,直线$BC切\odot O于点C$,$PD是\odot O的直径∠A= 22^{\circ}$,$∠B= 32^{\circ}$,$∠PDC= $.

答案： 解：连接OC。
∵直线BC切⊙O于点C，
∴OC⊥BC，∠OCB=90°。
∵∠B=32°，
∴∠BOC=90°-∠B=58°。
∵∠A=22°，∠A+∠ADC=∠BOC，
∴∠ADC=∠BOC-∠A=58°-22°=36°。
∵PD是⊙O的直径，
∴∠PCD=90°。
∴∠PDC=90°-∠ADC=90°-36°=54°。
54°

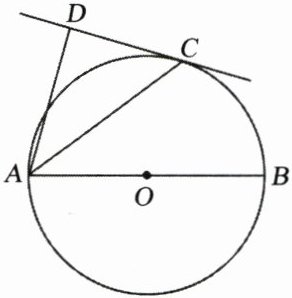
10. 如图,$AB为\odot O$的直径,$C为\odot O$上一点,$AD和过点C$的切线互相垂直,垂足为$D$.
(1) 求证:$AC平分∠DAB$;
(2) 若$CD= 4$,$AD= 8$,求$\odot O$的半径.

答案：
(1)证明：连接OC。
∵CD是⊙O的切线，
∴OC⊥CD。
∵AD⊥CD，
∴AD//OC，
∴∠DAC=∠OCA。
∵OA=OC，
∴∠OAC=∠OCA，
∴∠DAC=∠OAC，即AC平分∠DAB。
(2)解：连接BC。
在Rt△ADC中，AC=√(AD²+CD²)=√(8²+4²)=4√5。
∵AB是⊙O直径，
∴∠ACB=90°，
∴∠ACB=∠ADC。
∵∠DAC=∠BAC，
∴△ADC∽△ACB，
∴AD/AC=AC/AB，即8/(4√5)=4√5/AB，解得AB=10，
∴⊙O的半径为5。

11. 如图,已知$\odot O是以坐标原点O$为圆心,$1$为半径的圆,$∠AOB= 45^{\circ}$.点$P在x$轴上运动,若过点$P且与OA平行的直线与\odot O$有公共点,设$P(x,0)$,则$x$的取值范围是$-√2 ≤ x ≤ √2$.

答案： 解：因为OA是∠AOB的一边，∠AOB=45°，且点O为坐标原点，所以OA所在直线的倾斜角为45°，其斜率为tan45°=1，故OA的方程为y=x。
过点P(x,0)且与OA平行的直线方程为y = x - x（此处应为y = x - x₀，其中x₀为点P的横坐标，即y = x - x），即y = x - x。
直线y = x - x与⊙O：x² + y² = 1有公共点，所以圆心O(0,0)到直线的距离d ≤ 半径1。
根据点到直线距离公式，直线Ax + By + C = 0到点(x₀,y₀)的距离为|Ax₀ + By₀ + C| / √(A² + B²)，直线y = x - x可化为x - y - x = 0，所以d = |0 - 0 - x| / √(1² + (-1)²) = |x| / √2。
则|x| / √2 ≤ 1，即|x| ≤ √2，解得-√2 ≤ x ≤ √2。
答案：-√2 ≤ x ≤ √2

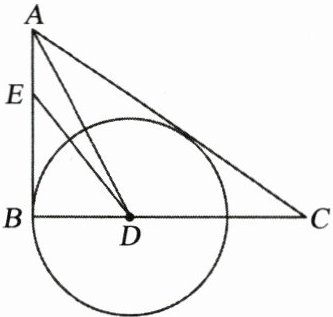
12. 如图,在$Rt△ABC$中,$∠B= 90^{\circ}$,$∠A的平分线交BC于点E$,$E为AB$上的一点,$DE= DC$,以点$D$为圆心,$DB长为半径作\odot D$.
(1) 求证:$AC是\odot D$的切线;
(2) 求证:$AB+EB= AC$.

答案： 【解析】：
(1)为了证明$AC$是$\odot D$的切线，我们可以按照以下步骤进行推导：
第一步，过点D作$DF \perp AC$于点F。
第二步，由于$AB$是$\odot D$的半径，且$AB \perp BC$，根据圆的切线性质，我们知道如果一条直线与圆的半径垂直，并且这条直线在圆上只与一个点接触，那么这条直线就是该圆的切线。
第三步，由于$AE$是$\angle BAC$的平分线，根据角平分线的性质，我们知道$DE=DF$（角平分线上的点到这个角的两边的距离相等）。
第四步，由于$DE$是$\odot D$的半径，且$DF \perp AC$，$DF=DE$，所以$AC$是$\odot D$的切线。
(2)为了证明$AB+EB=AC$，我们可以按照以下步骤进行推导：
第一步，由于$DF \perp AC$，且$DF=DB$（根据第一问的推导），根据直角三角形的全等性质，我们可以得出$Rt \bigtriangleup ADF \cong Rt \bigtriangleup ADB$（HL）。
第二步，由于$Rt \bigtriangleup ADF \cong Rt \bigtriangleup ADB$，根据全等三角形的对应边相等，我们可以得出$AF=AB$。
第三步，同理，由于$DE=DC$，且$DF \perp AC$，我们可以得出$Rt \bigtriangleup CDF \cong Rt \bigtriangleup EDB$（HL）。
第四步，由于$Rt \bigtriangleup CDF \cong Rt \bigtriangleup EDB$，根据全等三角形的对应边相等，我们可以得出$CF=EB$。
第五步，由于$AC=AF+CF$，根据第二步和第四步的结论，我们可以得出$AC=AB+EB$。
【答案】：
(1)证明见解析，$AC$是$\odot D$的切线。
(2)证明见解析，$AB+EB=AC$。