《2025年创新课时作业本九年级数学上册苏州专版》

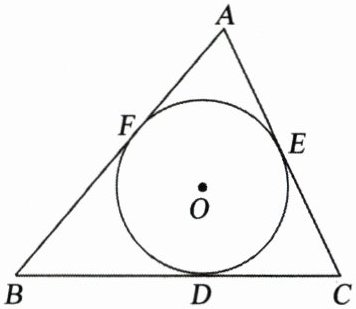
8. 如图,$\triangle ABC$是一张周长为18 cm的三角形纸片,$BC= 5$ cm,$\odot O$是它的内切圆,小明准备用剪刀在$\odot O$的右侧沿着与$\odot O$相切的任意一条直线MN剪下$\triangle AMN$,则剪下的三角形的周长为 (B)
A.13 cm
B.8 cm
C.6.5 cm
D.随直线$MN$的变化而变化

答案： 【解析】：本题可根据圆的切线长定理来求解剪下的$\triangle AMN$的周长。
圆的切线长定理：从圆外一点引圆的两条切线，它们的切线长相等。
设$\odot O$与$AB$、$BC$、$AC$、$MN$分别相切于点$D$、$E$、$F$、$G$。
根据切线长定理可得：$AD = AG$，$BD = BE$，$CE = CF$，$MG = MD$，$NG = NF$。
$\triangle AMN$的周长为$AM + AN + MN$，将$MN = MG + NG$代入可得：
$\triangle AMN$的周长$= AM + AN + MG + NG$。
因为$MG = MD$，$NG = NF$，所以$\triangle AMN$的周长$= AM + MD + AN + NF$。
又因为$AM + MD = AD$，$AN + NF = AF$，所以$\triangle AMN$的周长$= AD + AF$。
而$AD = AG$，$AF = AE$（切线长定理），所以$\triangle AMN$的周长$= AG + AE$。
$\triangle ABC$的周长为$AB + BC + AC$，$AB = AD + BD$，$AC = AF + CF$，则$\triangle ABC$的周长$=(AD + BD)+(BE + CE)+(AE + AF)$。
由$BD = BE$，$CE = CF$，可得$\triangle ABC$的周长$= (AD + AE)+(BD + BE)+(CE + CF)= (AD + AE)+2BC$。
已知$\triangle ABC$周长为$18cm$，$BC = 5cm$，则$AD + AE=\triangle ABC$的周长$- 2BC = 18 - 2×5 = 8cm$。
因为$\triangle AMN$的周长$= AG + AE = AD + AE$，所以$\triangle AMN$的周长为$8cm$。
【答案】：B

9. (1)直角三角形的两条直角边分别是5和12,则它的外接圆半径为$\frac{13}{2}$,内切圆半径为2。
(2)边长为$2\sqrt {3}$的等边$\triangle ABC$的外接圆的半径为2,内切圆半径为1。

答案： 【解析】：
本题主要考查直角三角形的外接圆半径和内切圆半径的计算，以及等边三角形的外接圆半径和内切圆半径的计算。
(1) 对于直角三角形，其外接圆的半径等于斜边的一半。由勾股定理，直角三角形的斜边长度为$\sqrt{5^2 + 12^2} = 13$，所以外接圆的半径为$\frac{13}{2}$。
内切圆半径则可以通过公式$r = \frac{a + b - c}{2}$计算，其中c为斜边长度，a和b为直角边长度。代入数值得到$r = \frac{5 + 12 - 13}{2} = 2$。
(2) 对于等边三角形，其外接圆的半径可以通过公式$R = \frac{a}{2\sin\frac{\pi}{3}}$计算，其中a为等边三角形的边长。代入$a = 2\sqrt{3}$，得到$R = \frac{2\sqrt{3}}{2\sin\frac{\pi}{3}} = 2$。
内切圆半径则可以通过公式$r = \frac{\sqrt{3}}{6}a$计算。代入$a = 2\sqrt{3}$，得到$r = \frac{\sqrt{3}}{6} × 2\sqrt{3} = 1$。
【答案】：
(1) $\frac{13}{2}$；2
(2) 2；1

10. 如图,$\triangle ABC外切于\odot O$,切点分别为$D$、$E$、$F$,$BC= 7$,$\odot O的半径为\sqrt {3}$,
(1)$∠A= 60^{\circ }$,求$\triangle ABC$的周长；
(2)若$∠A= 70^{\circ }$,$M为\odot O上异于F$、$E$的动点,则$∠FME$的度数为____。

(1)解：连接OE、OF、OA，设AF=AE=x。
∵△ABC外切于⊙O，切点为D、E、F，
∴OE⊥AC，OF⊥AB，OE=OF=√3，
∠OAF=∠OAE=1/2∠A=30°。
在Rt△AOF中，tan∠OAF=OF/AF，
即tan30°=√3/x，x=√3/tan30°=3。
设BD=BF=m，CD=CE=n，
则BF+CE=BD+CD=BC=7，
△ABC周长=AB+BC+AC=(AF+BF)+BC+(AE+CE)=2x+2(m+n)=2×3+2×7=20。
(2)55°或125°

答案：
(1)解：连接OE、OF、OA，设AF=AE=x。
∵△ABC外切于⊙O，切点为D、E、F，
∴OE⊥AC，OF⊥AB，OE=OF=√3，
∠OAF=∠OAE=1/2∠A=30°。
在Rt△AOF中，tan∠OAF=OF/AF，
即tan30°=√3/x，x=√3/tan30°=3。
设BD=BF=m，CD=CE=n，
则BF+CE=BD+CD=BC=7，
△ABC周长=AB+BC+AC=(AF+BF)+BC+(AE+CE)=2x+2(m+n)=2×3+2×7=20。
(2)55°或125°

11. 如图,在$\triangle ABC$中,$∠ACB= 70^{\circ }$,$\triangle ABC的内切圆\odot O与AB$、$BC分别相切于点D$、$E$,连接$DE$,$AO的延长线交DE于点F$,则$∠AFD= $55°。

答案： 解：连接OD、OE、OC。
∵⊙O是△ABC的内切圆，D、E为切点，
∴OD⊥AB，OE⊥BC，OD=OE，
AO平分∠BAC，CO平分∠ACB。
∵∠ACB=70°，
∴∠OCE=∠OCA=35°。
设∠OAD=∠OAC=α，则∠B=180°-∠BAC-∠ACB=180°-2α-70°=110°-2α。
在四边形ODBE中，∠ODB=∠OEB=90°，
∴∠DOE=180°-∠B=180°-(110°-2α)=70°+2α。
∵OD=OE，
∴∠ODE=∠OED=(180°-∠DOE)/2=(180°-70°-2α)/2=55°-α。
∵∠ODA=90°，
∴∠FDO=∠ODA-∠ODE=90°-(55°-α)=35°+α。
在Rt△AOD中，∠AOD=90°-α，
∴∠FOD=180°-∠AOD=180°-(90°-α)=90°+α。
在△FDO中，∠AFD=180°-∠FDO-∠FOD=180°-(35°+α)-(90°+α)=55°。
55°

12. 从三角形木板上截下一块圆形的木板。
(1)怎样才能使圆的面积尽可能大？(不写作法,但要保留作图痕迹)
(2)若$\triangle ABC的三边长为AB= 4$,$BC= 5$,$AC= 6$,求$\triangle ABC$的面积；
(3)在(1)(2)的基础上,求最大圆形木板的半径。

答案： 【解析】：本题主要考查了三角形内切圆的性质以及海伦公式和三角形面积与内切圆半径的关系。
（1）要使圆的面积尽可能大，则这个圆应该是三角形的内切圆，即圆与三角形三边都相切。
（2）对于三角形面积，可以使用海伦公式来计算。
海伦公式为：$S = \sqrt{p(p - a)(p - b)(p - c)}$，其中$a, b, c$是三角形的三边长，$p$是半周长，即$p = \frac{a + b + c}{2}$。
（3）三角形面积也可以表示为$S = pr$，其中$p$是半周长，$r$是内切圆半径。通过这个公式可以求出内切圆的半径。
【答案】：
(1)作图痕迹为三角形的内切圆（图略）；
(2)$p = \frac{4 + 5 + 6}{2} = \frac{15}{2}$
$S = \sqrt{\frac{15}{2}(\frac{15}{2} - 4)(\frac{15}{2} - 5)(\frac{15}{2} - 6)} = \sqrt{\frac{15}{2} × \frac{7}{2} × \frac{5}{2} × \frac{3}{2}} = \frac{15\sqrt{7}}{4}$
(3)由$S = pr$，得$r = \frac{S}{p} = \frac{\frac{15\sqrt{7}}{4}}{\frac{15}{2}} = \frac{\sqrt{7}}{2}$。
故最大圆形木板的半径为$\frac{\sqrt{7}}{2}$。