《2025年创新课时作业本九年级数学上册苏州专版》

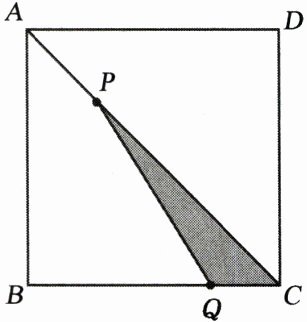
7. 如图,在正方形ABCD中,$AB= 5cm$,动点P以$\sqrt {2}cm/s$的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发,沿CB向点B移动,设P、Q两点移动时间为$ts(0＜t＜5)$.在P、Q两点移动的过程中,PQ的长度能否等于$\sqrt {10}cm$? 若能,求出此时t的值;若不能,请说明理由.

答案： 解：在正方形ABCD中，∠B=90°，AB=BC=5cm，AC为对角线，
∴AC=√(AB²+BC²)=√(5²+5²)=5√2cm，∠ACB=45°。
由题意得：AP=√2 t cm，CQ=t cm，
∴PC=AC-AP=5√2 - √2 t = √2(5 - t) cm。
过点P作PH⊥BC于点H，
在Rt△PHC中，∠PCH=45°，PC=√2(5 - t) cm，
∴PH=PC·sin45°=√2(5 - t)·√2/2=(5 - t) cm，
CH=PC·cos45°=√2(5 - t)·√2/2=(5 - t) cm，
∵CQ=t cm，
∴HQ=CH - CQ=(5 - t) - t=(5 - 2t) cm。
在Rt△PHQ中，PH=(5 - t) cm，HQ=(5 - 2t) cm，PQ=√10 cm，
由勾股定理得：PH² + HQ² = PQ²，
即(5 - t)² + (5 - 2t)² = (√10)²，
整理得：25 - 10t + t² + 25 - 20t + 4t² = 10，
5t² - 30t + 40 = 0，
t² - 6t + 8 = 0，
解得t₁=2，t₂=4。
∵0＜t＜5，
∴t=2和t=4均符合题意。
答：PQ的长度能等于√10 cm，此时t的值为2或4。

8. 如图,这是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点……第n行有n个点……前n行的点数和不能是以下哪个结果 ( B )
A.741
B.600
C.465
D.300

答案： 【解析】：
这个问题是一个三角点阵问题，其中前n行的点数和可以表示为等差数列的前n项和，即$1 + 2 + 3 + ... + n$。
等差数列的前n项和公式为：$S_n = \frac{n(n + 1)}{2}$。
我们需要判断哪个选项不能表示为这种形式。
A. $741$，
$\frac{n(n + 1)}{2} =741$，
$n(n + 1) = 1482$，
$n \approx 38.01$(此值不是整数，但由于浮点数的精度问题，我们可能需要进一步验证)，
经过验证，$n=38$时，$S_{38}=\frac{38 × 39}{2}=741$，是可以的。
B. $600$，
$\frac{n(n + 1)}{2} = 600$，
$n(n + 1) = 1200$，
此方程没有整数解，因为$34 × 35 = 1190$，$35 × 36 = 1260$，都不等于1200。
C. $465$，
$\frac{n(n + 1)}{2} = 465$，
$n(n + 1) = 930$，
$n \approx 30.49$(同样，需要验证)，
经过验证，$n=30$时，$S_{30}=\frac{30 × 31}{2}=465$，是可以的。
D. $300$，
$\frac{n(n + 1)}{2} = 300$，
$n(n + 1) = 600$，
$n = 24$(因为$24 × 25 = 600$)，
所以$n=24$时，这是可以的。
【答案】：
B.600。

9. 如图,在$△ABC$中,$∠B= 90^{\circ },AB= BC= 10cm$,点P从点A出发沿射线AB以1cm/s的速度作直线运动,点Q从点C出发沿边BC的延长线以2cm/s的速度作直线运动,如果P、Q分别从A、B同时出发,经过____4或6或12s,$△PCQ的面积为24cm^{2}$.

答案： 解：设经过$ t $秒，$\triangle PCQ$的面积为$24\,\text{cm}^2$。
由题意得：$AP = t\,\text{cm}$，$CQ = 2t\,\text{cm}$，$AB = BC = 10\,\text{cm}$，则$BP=\vert AB - AP\vert=\vert10 - t\vert\,\text{cm}$。
$\triangle PCQ$的面积为$\frac{1}{2} × CQ × BP$，即$\frac{1}{2} × 2t × \vert10 - t\vert=24$，化简得$t\vert10 - t\vert=24$。
情况1：当$0 \leq t \leq 10$时，$BP = 10 - t$
方程为$t(10 - t)=24$，即$t^2 - 10t + 24 = 0$。
解得$t_1 = 4$，$t_2 = 6$，均符合题意。
情况2：当$t ＞ 10$时，$BP = t - 10$
方程为$t(t - 10)=24$，即$t^2 - 10t - 24 = 0$。
解得$t_3 = 12$，$t_4 = -2$（舍去）。
综上，$t = 4$或$6$或$12$。
答案：$4$或$6$或$12$

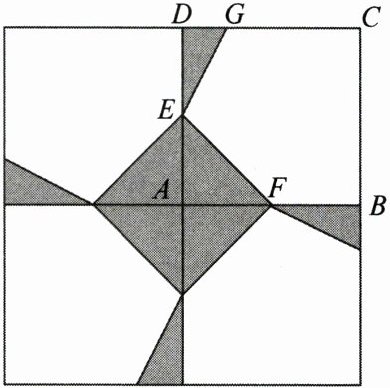
10. 如图,一个边长为8m的正方形花坛由4块全等的小正方形组成.在小正方形ABCD中,点G、E、F分别在CD、AD、AB上,且$DG= 1m,AE= AF= x$,在$△AEF,△DEG$,五边形EFBCG三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元.
(1) 当$x= 2$时,小正方形ABCD种植花卉所需的费用;
(2) 试用含有x的代数式表示五边形EFBCG的面积;
(3) 当x为何值时,大正方形花坛种植花卉所需的总费用是715元?

答案：
(1) 解：大正方形边长为8m，由4块全等小正方形组成，小正方形边长为4m。
当$x=2$时，
${S}_{\triangle AEF}=\frac{1}{2}AE\cdot AF=\frac{1}{2}× 2× 2=2{\text{m}}^{2}$，
$DE=AD - AE=4 - 2=2\text{m}$，$DG=1\text{m}$，
${S}_{\triangle DEG}=\frac{1}{2}DE\cdot DG=\frac{1}{2}× 2× 1=1{\text{m}}^{2}$，
${S}_{\text{五边形}EFBCG}={S}_{\text{小正方形}ABCD}-{S}_{\triangle AEF}-{S}_{\triangle DEG}=4× 4 - 2 - 1=13{\text{m}}^{2}$，
费用：$2× 20 + 1× 20 + 13× 10=40 + 20 + 130=190$元。
(2) 解：${S}_{\triangle AEF}=\frac{1}{2}{x}^{2}$，
$DE=4 - x$，${S}_{\triangle DEG}=\frac{1}{2}(4 - x)× 1=\frac{4 - x}{2}$，
${S}_{\text{五边形}EFBCG}=16 - \frac{1}{2}{x}^{2}-\frac{4 - x}{2}=-\frac{1}{2}{x}^{2}+\frac{1}{2}x + 14$。
(3) 解：一个小正方形费用：$20× (\frac{1}{2}{x}^{2}+\frac{4 - x}{2}) + 10× (-\frac{1}{2}{x}^{2}+\frac{1}{2}x + 14)=5{x}^{2}+5x + 120$，
总费用：$4× (5{x}^{2}+5x + 120)=715$，
整理得$20{x}^{2}+20x + 480=715$，即$4{x}^{2}+4x - 47=0$，
解得$x=\frac{-1\pm \sqrt{48}}{2}$（负值舍去），$x=\frac{-1 + 4\sqrt{3}}{2}$。
答：
(1) 190元；
(2) $-\frac{1}{2}{x}^{2}+\frac{1}{2}x + 14$；
(3)$x=\frac{-1 + 4\sqrt{3}}{2}$。