《2025年创新课时作业本九年级数学上册苏州专版》

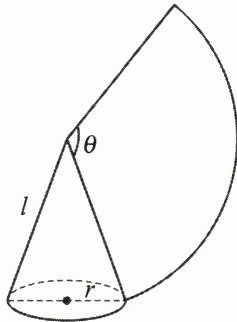
1. 若圆锥的母线长为 $ l $,底面圆的半径为 $ r $,则 $ S_{\text{圆锥侧}} = $ $\pi r l$.
2. 如图,圆锥与它的侧面展开图扇形之间存在着三种相等关系：
(1) 圆锥母线长 $ = $ 扇形半径；
(2) 圆锥底面圆周长 $ = $ 扇形弧长；
(3) 圆锥的侧面积 $ = $ 扇形面积.

答案： 【解析】：
本题主要考察圆锥侧面积的计算以及圆锥与其侧面展开图扇形之间的关系。
第一问，要求圆锥的侧面积，可以使用圆锥侧面积的公式，即$S_{\text{圆锥侧}} = \pi r l$，其中$r$是底面圆的半径，$l$是圆锥的母线长。
第二问，考察圆锥与扇形之间的三种相等关系：
圆锥的母线长等于扇形的半径。
圆锥的底面圆周长等于扇形的弧长。
圆锥的侧面积等于扇形的面积。
【答案】：
1. $\pi r l$；
2.
(1) 半径；
(2) 弧长；
(3) 面积。

1. 已知圆锥的底面半径为 $ 4 \text{ cm} $,母线长为 $ 5 \text{ cm} $,则圆锥的侧面积是 (B)
A.$ 20 \text{ cm}^2 $
B.$ 20\pi \text{ cm}^2 $
C.$ 10 \text{ cm}^2 $
D.$ 10\pi \text{ cm}^2 $

答案： 【解析】：
本题主要考察圆锥侧面积的计算。
圆锥的侧面积公式为：$S = \pi r l$，其中$r$为底面半径，$l$为母线长。
根据题意，底面半径$r = 4 \text{ cm}$，母线长$l = 5 \text{ cm}$。
代入公式得：$S = \pi × 4 × 5 = 20\pi \text{ cm}^2$。
【答案】：
B. $20\pi \text{ cm}^2$。

2. 若用半径为 $ 6 $,圆心角为 $ 120^{\circ} $ 的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为 (B)
A.$ 1 $
B.$ 2 $
C.$ 3 $
D.$ 4 $

答案： 【解析】：
本题主要考察圆锥的侧面积与扇形面积之间的关系。圆锥的侧面展开后是一个扇形，扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长。
首先，计算扇形的弧长。扇形弧长公式为：$弧长 = \frac{圆心角}{360^{\circ}} × 2\pi × 半径$。
给定扇形的半径为6，圆心角为$120^{\circ}$，所以扇形的弧长为：
$弧长 = \frac{120^{\circ}}{360^{\circ}} × 2\pi × 6 = \frac{1}{3} × 12\pi = 4\pi$。
由于这个弧长等于圆锥底面的周长，所以有：
$2\pi r = 4\pi$，
其中r是圆锥的底面半径。
解这个方程，得到：
$r = 2$。
【答案】：B. $2$。

3. 已知圆锥的底面半径为 $ 1 $,母线长为 $ 3 $,则该圆锥侧面展开图扇形的圆心角是 (B)
A.$ 90^{\circ} $
B.$ 120^{\circ} $
C.$ 180^{\circ} $
D.$ 150^{\circ} $

答案： 【解析】：
本题考查圆锥的侧面展开图扇形的圆心角计算。
首先，我们知道圆锥的底面半径为1，所以底面的周长，也即扇形的弧长为：
$C = 2\pi r = 2\pi × 1 = 2\pi$
设圆锥侧面展开图扇形的圆心角为 $n^{\circ}$，由于圆锥的母线长为3，所以扇形的半径也为3。
根据扇形的弧长与圆心角的关系，我们有：
$\frac{n\pi × 3}{180} = 2\pi$
解这个方程，我们得到：
$n = 120$
所以，圆锥侧面展开图扇形的圆心角为 $120^{\circ}$。
【答案】：
B. $120^{\circ}$。

4. 已知圆锥的侧面积为 $ 10\pi \text{ cm}^2 $,母线长为 $ 5 \text{ cm} $,则该圆锥的底面半径为 ______ $ \text{cm} $.
2

答案： 解：设圆锥的底面半径为 $ r $ cm。
圆锥侧面积公式为 $ S = \pi r l $（其中 $ l $ 为母线长）。
已知 $ S = 10\pi $ cm²，$ l = 5 $ cm，代入公式得：
$ 10\pi = \pi × r × 5 $
两边同时除以 $ \pi $：$ 10 = 5r $
解得 $ r = 2 $
2

5. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 $ r = 4 $,扇形的圆心角 $ \theta = 120^{\circ} $,则该圆锥母线 $ l $ 的长为 ______ 12.

答案： 【解析】：本题主要考查圆锥的侧面积计算以及弧长公式的应用。
圆锥的底面是一个圆，其周长即为扇形的弧长。
先求底面圆的周长：
圆的周长公式为 $C = 2\pi r$。
代入 $r = 4$，得到 $C = 2\pi × 4 = 8\pi$。
再利用扇形的弧长公式求母线长 $l$：
扇形的弧长公式为 $\text{弧长} = \frac{\theta}{360} × 2\pi l$。
已知扇形的圆心角 $\theta = 120^\circ$ 和弧长等于底面圆的周长 $8\pi$，代入公式得：
$\frac{120}{360} × 2\pi l = 8\pi$
化简得：
$\frac{1}{3} × 2\pi l = 8\pi$
$\frac{2\pi l}{3} = 8\pi$
$2\pi l = 24\pi$
$l = 12$
【答案】：12。

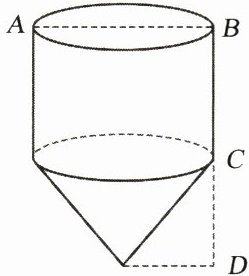
6. “赶陀螺”是一项深受人们喜爱的运动,如图是一个陀螺的立体结构图.已知底面圆的直径 $ AB = 8 \text{ cm} $,圆柱的高 $ BC = 6 \text{ cm} $,圆锥的高 $ CD = 3 \text{ cm} $,求这个陀螺的表面积.

答案： 【解析】：本题主要考查了圆锥的侧面积公式和圆柱的侧面积公式，熟练其公式是解题的关键。
首先，我们可以根据圆的面积公式求出底面圆的面积。
然后，我们可以根据圆柱的侧面积公式求出圆柱的侧面积。
接着，我们可以利用勾股定理求出圆锥的母线长。
最后，我们可以根据圆锥的侧面积公式求出圆锥的侧面积，将底面圆的面积、圆柱的侧面积和圆锥的侧面积相加，即可得到陀螺的表面积。
【答案】：
解：
底面圆的半径为$\frac{AB}{2} = \frac{8}{2} = 4（\text{cm}）$，
所以底面圆的面积$S_{\text{底}} = \pi r^2 = \pi × 4^2 = 16\pi （\text{cm}^2）$，
圆柱的侧面积$S_{\text{圆柱侧}} = 2\pi r h_{1} = 2\pi × 4 × 6 = 48× 2\pi ÷2= 48\pi（\text{cm}^2）$，
圆锥的母线长$l$可以通过勾股定理求出，即$l = \sqrt{r^2 + h_{2}^2} = \sqrt{4^2 + 3^2} = 5（\text{cm}）$，
圆锥的侧面积$S_{\text{圆锥侧}} = \pi r l = \pi × 4 × 5 = 20\pi （\text{cm}^2）$，
所以，陀螺的表面积$S = S_{\text{底}} + S_{\text{圆柱侧}} + S_{\text{圆锥侧}} = 16\pi + 48\pi + 20\pi = 84\pi（\text{cm}^2）$。
答：这个陀螺的表面积是$84\pi \text{cm}^2$。

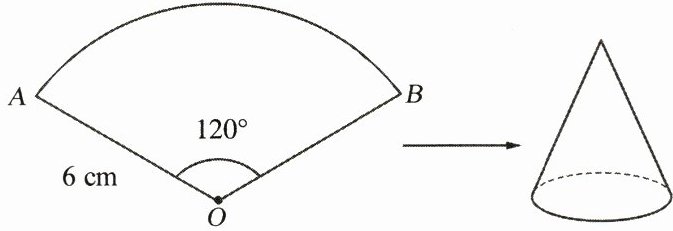
7. 如图,已知扇形 $ AOB $ 的半径为 $ 6 \text{ cm} $,圆心角的度数为 $ 120^{\circ} $,若将此扇形围成一个圆锥,则
(1) 围成的圆锥的侧面积为多少？
(2) 该圆锥的底面半径是多少？

答案： 【解析】：本题主要考查了圆锥的侧面积和底面半径的计算。
（1）首先，我们需要计算扇形的弧长。
根据弧长公式：$l = \frac{n\pi r}{180}$，其中$n$是圆心角的度数，$r$是半径。
将$n = 120^\circ$和$r = 6 \text{ cm}$代入公式，得到：
$l = \frac{120\pi × 6}{180} = 4\pi \text{ cm}$，
由于扇形围成的圆锥的侧面展开图就是扇形本身，所以圆锥的侧面积就等于扇形的面积。
根据扇形面积公式：$S = \frac{1}{2}lr$，其中$l$是弧长，$r$是半径。
代入$l = 4\pi \text{ cm}$和$r = 6 \text{ cm}$，得到：
$S = \frac{1}{2} × 4\pi × 6 = 12\pi \text{ cm}^2$，
所以围成的圆锥的侧面积为$12\pi \text{ cm}^2$。
（2）圆锥的底面周长等于扇形的弧长，即$4\pi \text{ cm}$。
根据圆的周长公式：$C = 2\pi r$，其中$C$是周长，$r$是半径。
设圆锥的底面半径为$r'$，则有：
$2\pi r' = 4\pi$，
解得$r' = 2 \text{ cm}$，
所以该圆锥的底面半径是$2 \text{ cm}$。
【答案】：
(1) $12\pi \text{ cm}^2$；
(2) $2 \text{ cm}$。