《2025年创新课时作业本九年级数学上册苏州专版》

8. 如图,$P$、$Q分别是\odot O的内接正五边形的边AB$、$BC$上的点,$BP= CQ$,则$∠POQ$的度数为 (C)
A.$75^{\circ }$
B.$54^{\circ }$
C.$72^{\circ }$
D.$60^{\circ }$

答案： 解：连接OA、OB、OC。
∵五边形ABCDE是⊙O的内接正五边形，
∴∠AOB=∠BOC=360°÷5=72°，OA=OB=OC，∠OBA=∠OCB。
∵BP=CQ，OB=OC，
∴△OBP≌△OCQ（SAS）。
∴∠BOP=∠COQ。
∵∠AOB=∠AOP+∠BOP=72°，
∴∠AOP+∠COQ=72°。
∴∠POQ=∠AOC - (∠AOP+∠COQ)=144° - 72°=72°。
答案：C

9. 刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积. 如图,若用圆的内接正十二边形的面积$S_{1}来近似估计\odot O的面积S$,设$\odot O$的半径为1,则$S-S_{1}= $$\pi - 3$.

答案： 【解析】：
本题要求用圆的内接正十二边形的面积$S_1$来近似估计圆的面积S，并求出它们之间的差值$S-S_1$，这需要分别计算出圆和内接正十二边形的面积。
对于半径为$r$的圆，其面积公式为$S = \pi r^2$，已知圆$O$的半径为$1$，将$r = 1$代入公式可得圆的面积$S=\pi×1^2=\pi$。
把圆$O$的内接正十二边形分成$12$个全等的等腰三角形，每个等腰三角形的顶角为$\frac{360^{\circ}}{12}=30^{\circ}$，腰长为圆的半径$1$。
根据三角形面积公式$S_{\triangle}=\frac{1}{2}ab\sin C$（其中$a,b$为三角形的两边，$C$为$a,b$夹角），对于每个等腰三角形，$a = b = 1$，$C = 30^{\circ}$，则每个等腰三角形的面积为：
$\frac{1}{2}×1×1×\sin30^{\circ}=\frac{1}{2}×1×1×\frac{1}{2}=\frac{1}{4}$。
那么内接正十二边形的面积$S_1$为$12$个这样的等腰三角形的面积之和，即$S_1 = 12×\frac{1}{4}=3$。
用圆的面积$S$减去内接正十二边形的面积$S_1$，可得$S - S_1=\pi - 3$。
【答案】：$\pi - 3$。

10. 如图,正方形$ABCD内接于\odot O$,$P为\overset{\frown}{BC}$上一点,连接$PD$、$PC$.
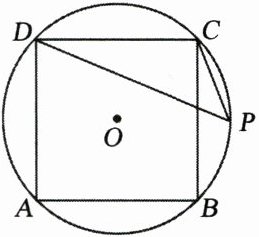
(1)$∠CPD= $45°；
(2)若$DC= 4$,$CP= 2\sqrt {2}$,求$DP$的长.解：连接BD。
∵正方形ABCD内接于⊙O，DC=4，
∴BD为⊙O直径，BD=4√2，∠BCD=90°，∠DBC=45°。
∵∠CPD=∠CBD=45°（同弧所对圆周角相等），
设DP=x，在△CPD中，由余弦定理得：
DC²=DP²+CP²-2·DP·CP·cos∠CPD
即4²=x²+(2√2)²-2·x·2√2·cos45°
16=x²+8-2·x·2√2·(√2/2)
16=x²+8-4x
x²-4x-8=0
解得x=2+2√3（负值舍去）
∴DP=2+2√3

答案：
(1) 45°
(2) 解：连接BD。
∵正方形ABCD内接于⊙O，DC=4，
∴BD为⊙O直径，BD=4√2，∠BCD=90°，∠DBC=45°。
∵∠CPD=∠CBD=45°（同弧所对圆周角相等），
设DP=x，在△CPD中，由余弦定理得：
DC²=DP²+CP²-2·DP·CP·cos∠CPD
即4²=x²+(2√2)²-2·x·2√2·cos45°
16=x²+8-2·x·2√2·(√2/2)
16=x²+8-4x
x²-4x-8=0
解得x=2+2√3（负值舍去）
∴DP=2+2√3

11. 如图,$AC是\odot O$的内接正六边形的一边,点$B在\overset{\frown}{AC}$上,且$BC是\odot O$的内接正十边形的一边,若$AB是\odot O的内接正n$边形的一边,则$n= $15.

答案： 解：设⊙O的半径为R。
∵AC是⊙O的内接正六边形的一边，
∴∠AOC = 360°/6 = 60°。
∵BC是⊙O的内接正十边形的一边，
∴∠BOC = 360°/10 = 36°。
∵点B在$\overset{\frown}{AC}$上，
∴∠AOB = ∠AOC - ∠BOC = 60° - 36° = 24°。
∵AB是⊙O的内接正n边形的一边，
∴n = 360°/∠AOB = 360°/24° = 15。
15

12. 如图,图①、图②、图③……图ⓝ分别是$\odot O的内接正三角形ABC$,正四边形$ABCD$、正五边形$ABCDE$……正$n边形ABCD…$,点$M$、$N分别从点B$、$C开始以相同的速度在\odot O$上逆时针运动.
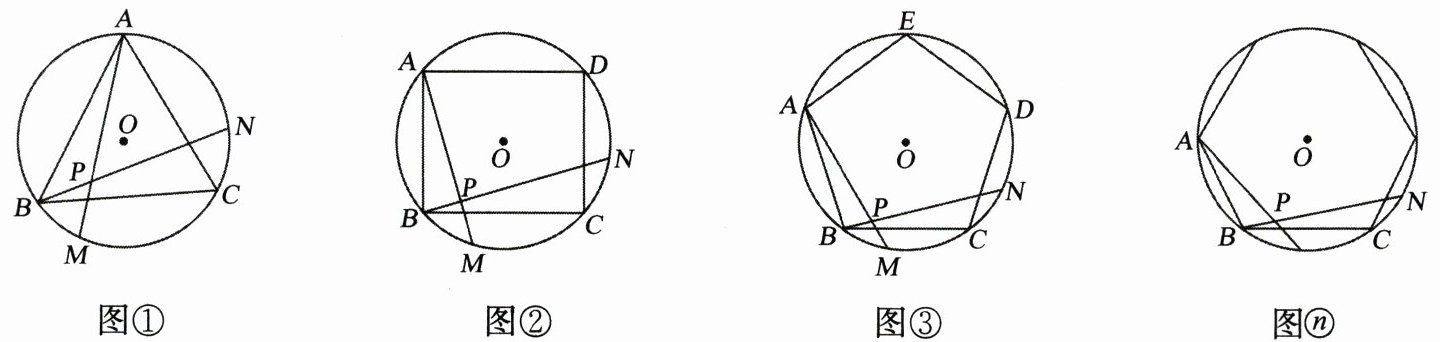
(1)图①中$∠APN$的度数为$60^\circ$；图②中,$∠APN$的度数为$90^\circ$,图③中$∠APN$的度数为$108^\circ$；
(2)试探索$∠APN的度数与正多边形边数n$的关系(直接写答案)$\frac{(n-2)×180^\circ}{n}$.

答案：
(1) $60^\circ$；$90^\circ$；$108^\circ$
(2) $\frac{(n-2)×180^\circ}{n}$