《2025年创新课时作业本九年级数学上册苏州专版》

8. 已知$\odot O$的直径为 8,点$P$在直线$l$上,且$OP=4$,则直线$l$与$\odot O$的位置关系是 (D)
A.相离
B.相切
C.相交
D.相切或相交

答案： 【解析】：
本题考查直线与圆的位置关系，需要利用圆心到直线的距离与圆的半径之间的关系来判断。
已知圆$\odot O$的直径为8，所以半径$r=4$。
点$P$在直线$l$上，且$OP=4$，即圆心$O$到点$P$的距离为4，这也等于圆的半径。
当$OP$垂直于直线$l$时，圆心$O$到直线$l$的距离$d$等于$OP$，即$d=4$，此时圆的半径$r$也等于4，因此直线$l$与圆$\odot O$相切。
当$OP$不垂直于直线$l$时，圆心$O$到直线$l$的距离$d$会小于$OP$，即$d＜4$，由于$d＜r$，所以直线$l$与圆$\odot O$相交。
综合上述两种情况，直线$l$与圆$\odot O$的位置关系是相切或相交。
【答案】：
D. 相切或相交。

9. 圆心$O$到直线$l$的距离为$d$,$\odot O$半径为$R$. 若$d$、$R$是方程$x^{2}-9x+20=0$的两根,则直线和圆的位置关系是相交,则$d$、$R$值分别为$d = 4$，$R = 5$;若$d$、$R$是方程$x^{2}-4x+m=0$的两个根,且直线$l$与$\odot O$相切,则$m$的值是$m = 4$.

答案： 【解析】：
本题主要考察直线与圆的位置关系以及一元二次方程的解。
首先，我们解方程$x^{2} - 9x + 20 = 0$，通过因式分解得到$(x-4)(x-5)=0$，解得$x_{1} = 4$，$x_{2} = 5$。
由于题目描述中，直线$l$与圆$\odot O$相交，根据直线与圆的位置关系，我们知道相交时圆心到直线的距离$d$应该小于圆的半径$R$。
因此，我们可以确定$d = 4$，$R = 5$。
接着，我们考虑第二个问题。
由于直线$l$与圆$\odot O$相切，根据直线与圆的位置关系，我们知道相切时圆心到直线的距离$d$应该等于圆的半径$R$。
又因为$d$和$R$是方程$x^{2} - 4x + m = 0$的两个根，根据一元二次方程的根与系数的关系，我们有$d + R = 4$，$d × R = m$。
由于$d = R$，我们可以得到$d = R = 2$。
最后，我们计算$m$的值，即$m = d × R = 2 × 2 = 4$。
【答案】：
$d = 4$，$R = 5$；$m = 4$。

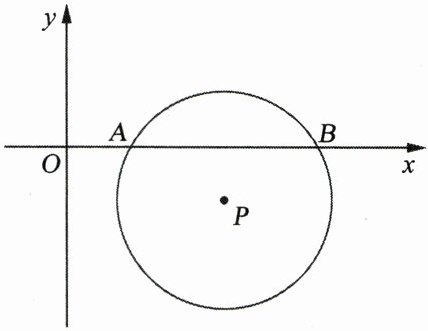
10. 如图,在平面直角坐标系中,$\odot P$与$x$轴交于$A$、$B$两点,点$P$的坐标为$(3,-1)$,$AB=2\sqrt{3}$.
(1) 求$\odot P$的半径;
(2) 将$\odot P$向下平移,求$\odot P$与$x$轴相切时平移的距离.

答案： 【解析】：
本题主要考查了垂径定理和直线与圆的位置关系。
（1）根据垂径定理，过圆心$P$作$x$轴的垂线，垂足为$C$，则$C$为$AB$的中点，即$AC = \frac{AB}{2} = \sqrt{3}$，利用勾股定理，可以求出圆的半径$R$，即$R = \sqrt{PC^{2} + AC^{2}}$，其中$PC$为圆心到$x$轴的距离，即$y$坐标的绝对值，$AC$为圆心横坐标到$A$或$B$的距离。
（2）当圆与$x$轴相切时，圆心到$x$轴的距离等于圆的半径，根据这个性质，可以求出平移的距离。
【答案】：
解：
(1)过点$P$作$PC \perp AB$于点$C$，
∵$P(3,-1)$，
∴$OC=3$，$PC=1$，
∵$AB=2\sqrt{3}$，
∴$AC=\sqrt{3}$，
连接$AP$，则$AP=\sqrt{AC^2+PC^2}=2$，
∴$\odot P$的半径为$2$。
(2)
∵$\odot P$的半径为$2$，
∴当$\odot P$向下平移$1$个单位时，$\odot P$与$x$轴相切，
∴平移的距离为$1$。

11. 以点$P(1,2)$为圆心,$r$为半径画圆,与坐标轴恰好有三个交点,则$r$应满足 (A)
A.$r=2$或$r=\sqrt{5}$
B.$r=2$
C.$r=\sqrt{5}$
D.$2\leqslant r\leqslant\sqrt{5}$

答案： 【解析】：
本题主要考察直线与圆的位置关系，特别是圆与坐标轴的交点情况。
首先，考虑圆心$P(1,2)$到$x$轴的距离。由于圆心$P$的$y$坐标为$2$，所以到$x$轴的距离为$2$。
其次，考虑圆心$P(1,2)$到$y$轴的距离。由于圆心$P$的$x$坐标为$1$，所以到$y$轴的距离为$1$。
现在，根据这些距离和给定的选项来确定$r$的值。
当$r=2$时，圆与$x$轴相切，并与$y$轴相交于两点（因为圆心到$y$轴的距离小于$r$），再加上圆与$x$轴的切点，共有三个交点。但我们需要检查是否还有其他可能的$r$值。
当$r=\sqrt{5}$时，由于$\sqrt{5}$大于圆心到$x$轴的距离$2$且大于圆心到$y$轴的距离$1$，并且$\sqrt{2^2+1^2}=\sqrt{5}$，即圆心到原点的距离等于$r$，此时圆会经过原点，并与$x$轴和$y$轴各相交于一点（除了原点外），再加上圆与$x$轴的另一个交点（不是切点），也是三个交点。
当$r$在$2$和$\sqrt{5}$之间时，圆会与$x$轴相交于两点（不是切点），并与$y$轴也相交于两点，共有四个交点，不符合题意。
当$r$大于$\sqrt{5}$时，圆会与$x$轴和$y$轴都相交于两点，并且还会包含其他点，交点数量超过三个。
当$r$小于$2$时，圆可能与$x$轴无交点或只有一个切点，并与$y$轴相交于两点，交点数量不足三个。
综上所述，只有当$r=2$或$r=\sqrt{5}$时，圆与坐标轴恰好有三个交点。
【答案】：
A. $r=2$或$r=\sqrt{5}$。

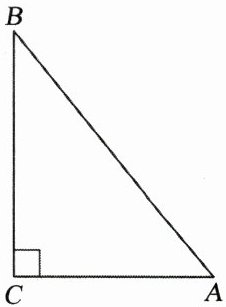
12. 在$\mathrm{Rt}\triangle ABC$中,$\angle C=90^{\circ}$,$BC=4\mathrm{cm}$,$AC=3\mathrm{cm}$. 以点$C$为圆心,$R$为半径作$\odot C$.
(1) 若边$AB$与$\odot C$没有公共点,求$r$的取值范围;
(2) 若边$AB$与$\odot C$有两个公共点,求$r$的取值范围;
(3) 若边$AB$与$\odot C$只有一个公共点,求$r$的取值范围.

答案： 【解析】：本题主要考查直线与圆的位置关系，可通过比较圆心到直线的距离$d$与圆半径$R$的大小关系来确定。
先根据勾股定理求出斜边$AB$的长度，再利用三角形面积公式求出圆心$C$到$AB$的距离$d$，最后根据直线与圆的位置关系分情况讨论$R$的取值范围。
步骤一：求斜边$AB$的长度
在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$BC = 4cm$，$AC = 3cm$，根据勾股定理$AB^{2}=AC^{2}+BC^{2}$，可得：
$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5cm$
步骤二：求圆心$C$到$AB$的距离$d$
根据三角形面积公式$S=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot d$（其中$S$为$\triangle ABC$的面积），可得：
$\frac{1}{2}×3×4=\frac{1}{2}×5× d$
$d=\frac{3×4}{5}=\frac{12}{5}=2.4cm$
步骤三：分情况讨论$R$的取值范围
（1）若边$AB$与$\odot C$没有公共点
当圆心到直线的距离$d\gt R$时，直线与圆相离，即边$AB$与$\odot C$没有公共点。
已知$d = 2.4cm$，且$R\gt0$（半径为正数），所以$0\lt R\lt 2.4$。
（2）若边$AB$与$\odot C$有两个公共点
当圆心到直线的距离$d\lt R$且$R\lt AC$（点$A$到圆心$C$的距离）时，直线与圆相交，即边$AB$与$\odot C$有两个公共点。
已知$d = 2.4cm$，$AC = 3cm$，所以$2.4\lt R\lt 3$。
（3）若边$AB$与$\odot C$只有一个公共点
当圆心到直线的距离$d = R$或$AC\leq R\lt BC$时，直线与圆相切或直线与圆相交但其中一个交点为直角顶点，即边$AB$与$\odot C$只有一个公共点。
已知$d = 2.4cm$，$AC = 3cm$，$BC = 4cm$，所以$R = 2.4$或$3\leq R\lt 4$。
【答案】：
(1)$0\lt R\lt 2.4$；
(2)$2.4\lt R\lt 3$；
(3)$R = 2.4$或$3\leq R\lt 4$