第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1. 一般地,将一组数据按大小顺序排列,如果数据的个数是奇数,那么处于
2. 一组数据中出现次数最多的数叫作这组数据的
中间
位置的数叫作这组数据的中位
数;如果数据的个数是偶数,那么处于中间位置的两个数的平均
数叫作这组数据的中位数。2. 一组数据中出现次数最多的数叫作这组数据的
众数
。
答案:
1. 中间;中位;平均
2. 众数
2. 众数
1. 一组数据3,4,4,5,5,5,6,6,7的众数是 (
A.4
B.5
C.6
D.7
B
)A.4
B.5
C.6
D.7
答案:
【解析】:
众数是一组数据中出现次数最多的数。我们需要统计每个数在这组数据中出现的次数。
数据$3$出现$1$次;
数据$4$出现$2$次;
数据$5$出现$3$次;
数据$6$出现$2$次;
数据$7$出现$1$次。
从上面的统计可以看出,数据$5$的出现次数最多,为$3$次。
【答案】:
B. $5$
众数是一组数据中出现次数最多的数。我们需要统计每个数在这组数据中出现的次数。
数据$3$出现$1$次;
数据$4$出现$2$次;
数据$5$出现$3$次;
数据$6$出现$2$次;
数据$7$出现$1$次。
从上面的统计可以看出,数据$5$的出现次数最多,为$3$次。
【答案】:
B. $5$
2. 九年级(1)班15名男同学进行引体向上测试,每人只测一次,测试结果统计如下:
|引体向上个数|0|1|2|3|4|5|6|7|8|
|人数|1|1|2|1|3|3|2|1|1|
这15名男同学引体向上数的中位数是 (
A.2
B.3
C.4
D.5
|引体向上个数|0|1|2|3|4|5|6|7|8|
|人数|1|1|2|1|3|3|2|1|1|
这15名男同学引体向上数的中位数是 (
C
)A.2
B.3
C.4
D.5
答案:
【解析】:
本题主要考查中位数的定义及计算方法。中位数是一组数据排序后位于中间的数。如果数据量为奇数,则中位数是中间的那个数;如果数据量为偶数,则中位数是中间两个数的平均值。
首先,将引体向上的个数按照从小到大的顺序排列,并考虑对应的人数:
$0(1人), 1(1人), 2(2人), 3(1人), 4(3人), 5(3人), 6(2人), 7(1人), 8(1人)$
然后,计算累计人数,以确定中位数所在的位置:
$1, 2, 4, 5, 8, 11, 13, 14, 15$
因为总共有15名同学,所以中位数应该是第8名同学的成绩(因为8是奇数,所以中位数就是第$\frac{15+1}{2}=8$个数)。
从上面的累计人数中,我们可以看到第8名同学的成绩是4个引体向上(因为第5到第8名同学都是4个引体向上)。
所以,这15名男同学引体向上数的中位数是4。
【答案】:
C
本题主要考查中位数的定义及计算方法。中位数是一组数据排序后位于中间的数。如果数据量为奇数,则中位数是中间的那个数;如果数据量为偶数,则中位数是中间两个数的平均值。
首先,将引体向上的个数按照从小到大的顺序排列,并考虑对应的人数:
$0(1人), 1(1人), 2(2人), 3(1人), 4(3人), 5(3人), 6(2人), 7(1人), 8(1人)$
然后,计算累计人数,以确定中位数所在的位置:
$1, 2, 4, 5, 8, 11, 13, 14, 15$
因为总共有15名同学,所以中位数应该是第8名同学的成绩(因为8是奇数,所以中位数就是第$\frac{15+1}{2}=8$个数)。
从上面的累计人数中,我们可以看到第8名同学的成绩是4个引体向上(因为第5到第8名同学都是4个引体向上)。
所以,这15名男同学引体向上数的中位数是4。
【答案】:
C
3. “江城读书月”活动结束后,对八年级(3)班45人所阅读书籍数量情况的统计结果如下表所示:
|阅读数量|1本|2本|3本|3本以上|
|人数|10|18|13|4|
根据统计结果,这里的数据2是这组数据的 (
A.平均数
B.中位数
C.众数
D.中位数、众数
|阅读数量|1本|2本|3本|3本以上|
|人数|10|18|13|4|
根据统计结果,这里的数据2是这组数据的 (
D
)A.平均数
B.中位数
C.众数
D.中位数、众数
答案:
【解析】:
本题考查中位数和众数的理解。
首先,将数据按照阅读数量进行排序:
1本:10人
2本:18人
3本:13人
3本以上:4人(由于“3本以上”是模糊数量,为了确定中位数和众数,可以将其视为大于3的某个具体数量,但在排序时,它仍然排在3本之后)
接下来,为了找到中位数,需要确定中间位置的数值。
因为有45个数据点,所以中位数将是第23个数据点(当数据点数量为奇数时,中位数是中间那个数;当数据点数量为偶数时,中位数是中间两个数的平均值,但在此问题中,由于我们直接通过人数来确定位置,所以直接找到第23个位置即可)。
从排序后的数据可以看出,第23个位置落在“2本”的范围内(前10+18=28人中,第23人是其中的一个),因此中位数是2本。
再来看众数,众数是出现次数最多的数值。
从数据中可以看出,“2本”的人数最多,有18人,所以众数也是2本。
由于2本既是中位数又是众数,所以答案是D,中位数和众数。但题目选项要求的是单一称呼,由于众数更具体且直接(即出现次数最多的数),而中位数虽然也是2,但在此情境下,若要选择一个最具代表性的称呼,通常选择众数,不过根据题目选项,需要选择包含正确答案的选项,所以选择D,它包含了“中位数”和“众数”两个正确的称呼。但根据常规理解,若必须单选,会倾向于选择“众数”作为最直接答案,但此题中需严格遵循题目给出的选项。
【答案】:D
本题考查中位数和众数的理解。
首先,将数据按照阅读数量进行排序:
1本:10人
2本:18人
3本:13人
3本以上:4人(由于“3本以上”是模糊数量,为了确定中位数和众数,可以将其视为大于3的某个具体数量,但在排序时,它仍然排在3本之后)
接下来,为了找到中位数,需要确定中间位置的数值。
因为有45个数据点,所以中位数将是第23个数据点(当数据点数量为奇数时,中位数是中间那个数;当数据点数量为偶数时,中位数是中间两个数的平均值,但在此问题中,由于我们直接通过人数来确定位置,所以直接找到第23个位置即可)。
从排序后的数据可以看出,第23个位置落在“2本”的范围内(前10+18=28人中,第23人是其中的一个),因此中位数是2本。
再来看众数,众数是出现次数最多的数值。
从数据中可以看出,“2本”的人数最多,有18人,所以众数也是2本。
由于2本既是中位数又是众数,所以答案是D,中位数和众数。但题目选项要求的是单一称呼,由于众数更具体且直接(即出现次数最多的数),而中位数虽然也是2,但在此情境下,若要选择一个最具代表性的称呼,通常选择众数,不过根据题目选项,需要选择包含正确答案的选项,所以选择D,它包含了“中位数”和“众数”两个正确的称呼。但根据常规理解,若必须单选,会倾向于选择“众数”作为最直接答案,但此题中需严格遵循题目给出的选项。
【答案】:D
4. 从小到大排列的一组数据:-2,0,4,4,x,6,6,9的中位数是5,那么这组数据的众数是
6
。
答案:
【解析】:
首先,需要明确中位数的定义。
对于一组从小到大排列的数据,如果数据量为奇数,则中位数是中间的那个数;
如果数据量为偶数,则中位数是中间两个数的平均值。
题目中给出的数据总数为8(偶数个),且中位数是5。
因此,中间两个数的平均值应为5。
数据从小到大排列为-2,0,4,4,x,6,6,9。
中间两个数为4,x或者x,6。
考虑到4和6的平均值不为5,而题目已给出中位数是5,所以x必须和4或6中的一个数配对,使得它们的平均值为5。
通过计算,$(4 + x) ÷ 2 = 5$ 或 $(x + 6) ÷ 2 = 5$,
可以得出$x = 6$(因为$x$应该大于4且小于6或者等于6,而等于其他值均不满足条件)。
然后,需要找出这组数据的众数。
众数是一组数据中出现次数最多的数。
在这组数据中,数字6出现了3次,而其他数字出现的次数都少于3次。
因此,众数是6。
【答案】:
6
首先,需要明确中位数的定义。
对于一组从小到大排列的数据,如果数据量为奇数,则中位数是中间的那个数;
如果数据量为偶数,则中位数是中间两个数的平均值。
题目中给出的数据总数为8(偶数个),且中位数是5。
因此,中间两个数的平均值应为5。
数据从小到大排列为-2,0,4,4,x,6,6,9。
中间两个数为4,x或者x,6。
考虑到4和6的平均值不为5,而题目已给出中位数是5,所以x必须和4或6中的一个数配对,使得它们的平均值为5。
通过计算,$(4 + x) ÷ 2 = 5$ 或 $(x + 6) ÷ 2 = 5$,
可以得出$x = 6$(因为$x$应该大于4且小于6或者等于6,而等于其他值均不满足条件)。
然后,需要找出这组数据的众数。
众数是一组数据中出现次数最多的数。
在这组数据中,数字6出现了3次,而其他数字出现的次数都少于3次。
因此,众数是6。
【答案】:
6
5. 已知一组数据6,x,3,3,5,1的众数是3和5,则这组数据的中位数是
4
。
答案:
【解析】:
首先,根据众数的定义,一组数据中出现次数最多的数为众数。
题目中给出数据组$6,x,3,3,5,1$的众数是3和5,意味着3和5在这组数据中出现的次数都是最多的,且次数相同。
由于3已经出现了两次,而5只出现了一次,为了使5也成为众数,x必须等于5。
确定$x=5$后,将这组数据从小到大排序得到:$1,3,3,5,5,6$。
因为数据组有6个数,所以中位数是第3个数和第4个数的平均值,即$(3+5)÷ 2=4$。
【答案】:
4
首先,根据众数的定义,一组数据中出现次数最多的数为众数。
题目中给出数据组$6,x,3,3,5,1$的众数是3和5,意味着3和5在这组数据中出现的次数都是最多的,且次数相同。
由于3已经出现了两次,而5只出现了一次,为了使5也成为众数,x必须等于5。
确定$x=5$后,将这组数据从小到大排序得到:$1,3,3,5,5,6$。
因为数据组有6个数,所以中位数是第3个数和第4个数的平均值,即$(3+5)÷ 2=4$。
【答案】:
4
6. 某兴趣小组20位同学在一次测试中的得分情况如下表:
|得分|10|9|8|7|
|人数|5|8|4|3|
(1) 写出这20位同学测试得分的中位数为
(2) 求这20位同学该次测试得分的平均分。
|得分|10|9|8|7|
|人数|5|8|4|3|
(1) 写出这20位同学测试得分的中位数为
9
,众数为9
;(2) 求这20位同学该次测试得分的平均分。
解:这20位同学的加权平均分为
$\text{平均分} = \frac{(10 × 5) + (9 × 8) + (8 × 4) + (7 × 3)}{20}$
$= \frac{50 + 72 + 32 + 21}{20}$
$= \frac{175}{20}$
$= 8.75 \text{(分)}$
答:这20位同学该次测试得分的平均分为8.75分。
$\text{平均分} = \frac{(10 × 5) + (9 × 8) + (8 × 4) + (7 × 3)}{20}$
$= \frac{50 + 72 + 32 + 21}{20}$
$= \frac{175}{20}$
$= 8.75 \text{(分)}$
答:这20位同学该次测试得分的平均分为8.75分。
答案:
【解析】:
(1)要求中位数和众数,需要首先对数据进行排序和统计。
中位数:将所有数值由小到大排列后正中间的数。如果数据量是奇数,中位数就是中间那个数;如果数据量是偶数,中位数是中间两个数的平均值。由于本题数据已经分组给出,我们需要根据每组的人数来确定中位数的位置。总共有20位同学,所以中位数应该是第10和第11位同学得分的平均值。从表格中可以看出,得分9的人数最多(8人),且从低到高排列后,第10和第11位同学均落在得分9的组内,因此中位数是9。
众数:出现次数最多的数。从表格中可以看出,得分9的人数最多,所以众数是9。
(2)要求平均分,需要使用加权平均数的公式,即每个数据点乘以它的权重(在这个案例中是每组的人数),然后将这些乘积相加,再除以总人数。
【答案】:
(1)中位数为9,众数为9。
(2)解:这20位同学的加权平均分为
$\text{平均分} = \frac{(10 × 5) + (9 × 8) + (8 × 4) + (7 × 3)}{20}$
$= \frac{50 + 72 + 32 + 21}{20}$
$= \frac{175}{20}$
$= 8.75 \text{(分)}$
答:这20位同学该次测试得分的平均分为8.75分。
(1)要求中位数和众数,需要首先对数据进行排序和统计。
中位数:将所有数值由小到大排列后正中间的数。如果数据量是奇数,中位数就是中间那个数;如果数据量是偶数,中位数是中间两个数的平均值。由于本题数据已经分组给出,我们需要根据每组的人数来确定中位数的位置。总共有20位同学,所以中位数应该是第10和第11位同学得分的平均值。从表格中可以看出,得分9的人数最多(8人),且从低到高排列后,第10和第11位同学均落在得分9的组内,因此中位数是9。
众数:出现次数最多的数。从表格中可以看出,得分9的人数最多,所以众数是9。
(2)要求平均分,需要使用加权平均数的公式,即每个数据点乘以它的权重(在这个案例中是每组的人数),然后将这些乘积相加,再除以总人数。
【答案】:
(1)中位数为9,众数为9。
(2)解:这20位同学的加权平均分为
$\text{平均分} = \frac{(10 × 5) + (9 × 8) + (8 × 4) + (7 × 3)}{20}$
$= \frac{50 + 72 + 32 + 21}{20}$
$= \frac{175}{20}$
$= 8.75 \text{(分)}$
答:这20位同学该次测试得分的平均分为8.75分。
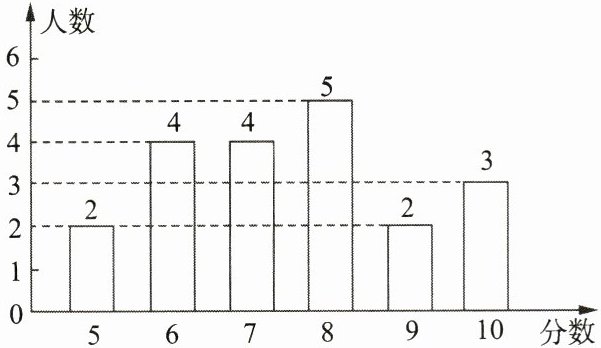
7. 为了解学生掌握垃圾分类知识的情况,某学校举行了一次“垃圾分类”知识的小测试,现随机抽取20名学生的测试成绩(满分10分,学生成绩均为整数)进行整理,并绘制成如下统计图。根据以上信息,解答下列问题:
(1) 这20名学生的测试成绩的中位数为
(2) 计算这20名学生的测试成绩的平均数;
(3) 该校共2400名学生参加了本次测试,试估计参加此次测试成绩不低于“平均水平”的学生人数。
(1) 这20名学生的测试成绩的中位数为
7.5
分,众数为8
分;(2) 计算这20名学生的测试成绩的平均数;
7.5分
(3) 该校共2400名学生参加了本次测试,试估计参加此次测试成绩不低于“平均水平”的学生人数。
1200人

答案:
1. (1)7.5,8
2. (2)
解:根据平均数公式$\overline{x}=\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots +x_{n}f_{n}}{f_{1}+f_{2}+\cdots +f_{n}}$(其中$x_{i}$是数据,$f_{i}$是数据$x_{i}$出现的次数)。
这里$x_{1}=5,f_{1}=2$;$x_{2}=6,f_{2}=4$;$x_{3}=7,f_{3}=4$;$x_{4}=8,f_{4}=5$;$x_{5}=9,f_{5}=2$;$x_{6}=10,f_{6}=3$。
则$\overline{x}=\frac{5×2 + 6×4+7×4 + 8×5+9×2+10×3}{2 + 4+4 + 5+2+3}$
先计算分子:$5×2 + 6×4+7×4 + 8×5+9×2+10×3=10 + 24+28 + 40+18+30$
$10 + 24+28 + 40+18+30=(10 + 24)+(28 + 40)+(18 + 30)=34+68+48 = 150$。
分母$=2 + 4+4 + 5+2+3=20$。
所以$\overline{x}=\frac{150}{20}=7.5$分。
3. (3)
解:成绩不低于平均水平($7.5$分)的有$8$分、$9$分、$10$分的人数。
$8$分的有$5$人,$9$分的有$2$人,$10$分的有$3$人,共$5 + 2+3=10$人。
则$20$人中成绩不低于平均水平的占比为$\frac{10}{20}=\frac{1}{2}$。
该校共$2400$名学生,所以估计成绩不低于平均水平的学生人数为$2400×\frac{1}{2}=1200$人。
综上,(1)中位数$7.5$分,众数$8$分;(2)平均数是$7.5$分;(3)估计成绩不低于平均水平的学生人数为$1200$人。
2. (2)
解:根据平均数公式$\overline{x}=\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots +x_{n}f_{n}}{f_{1}+f_{2}+\cdots +f_{n}}$(其中$x_{i}$是数据,$f_{i}$是数据$x_{i}$出现的次数)。
这里$x_{1}=5,f_{1}=2$;$x_{2}=6,f_{2}=4$;$x_{3}=7,f_{3}=4$;$x_{4}=8,f_{4}=5$;$x_{5}=9,f_{5}=2$;$x_{6}=10,f_{6}=3$。
则$\overline{x}=\frac{5×2 + 6×4+7×4 + 8×5+9×2+10×3}{2 + 4+4 + 5+2+3}$
先计算分子:$5×2 + 6×4+7×4 + 8×5+9×2+10×3=10 + 24+28 + 40+18+30$
$10 + 24+28 + 40+18+30=(10 + 24)+(28 + 40)+(18 + 30)=34+68+48 = 150$。
分母$=2 + 4+4 + 5+2+3=20$。
所以$\overline{x}=\frac{150}{20}=7.5$分。
3. (3)
解:成绩不低于平均水平($7.5$分)的有$8$分、$9$分、$10$分的人数。
$8$分的有$5$人,$9$分的有$2$人,$10$分的有$3$人,共$5 + 2+3=10$人。
则$20$人中成绩不低于平均水平的占比为$\frac{10}{20}=\frac{1}{2}$。
该校共$2400$名学生,所以估计成绩不低于平均水平的学生人数为$2400×\frac{1}{2}=1200$人。
综上,(1)中位数$7.5$分,众数$8$分;(2)平均数是$7.5$分;(3)估计成绩不低于平均水平的学生人数为$1200$人。
查看更多完整答案,请扫码查看


