《2025年创新课时作业本九年级数学上册苏州专版》

一般地,设一个试验的所有可能发生的结果有n个,它们都是随机事件,每次试验有且只有其中的1个结果出现。如果每个结果出现的机会相等,那么我们说这n个事件的发生是等可能的,也称这个试验的结果具有等可能性。

答案： 【解析】：本题主要考查等可能性试验的基本概念。
根据等可能性试验的定义，一个试验的所有可能发生的结果有n个，且这些结果都是随机事件。在每次试验中，有且只有其中的一个结果会出现。如果每个结果出现的机会相等，那么就说这n个事件的发生是等可能的，也称这个试验的结果具有等可能性。
【答案】：1；相等；等可能的；等可能性。

1. 下列各组事件中,不属于等可能事件的是(C)
A.投掷一枚均匀的硬币,正面朝上或反面朝上
B.投掷一枚均匀的标准骰子,4点朝上或6点朝上
C.从一副扑克中随机摸一张牌,摸到的是5或大王
D.从一副扑克中随机摸一张牌,摸到的是5或6

答案： 【解析】：
本题考查的是等可能性事件的概念。等可能性事件意味着每一个事件发生的概率是相等的。
A选项：投掷一枚均匀的硬币，正面朝上或反面朝上。由于硬币是均匀的，所以正面和反面朝上的概率都是$\frac{1}{2}$，属于等可能事件。
B选项：投掷一枚均匀的标准骰子，4点朝上或6点朝上。由于骰子是均匀的，所以4点和6点朝上的概率都是$\frac{1}{6}$，属于等可能事件。
C选项：从一副扑克中随机摸一张牌，摸到的是5或大王。一副扑克中有4张5和1张大王，所以摸到5的概率是$\frac{4}{54}$，而摸到大王的概率是$\frac{1}{54}$，这两个概率不相等，所以不属于等可能事件。
D选项：从一副扑克中随机摸一张牌，摸到的是5或6。一副扑克中有4张5和4张6，所以摸到5或6的概率都是$\frac{4}{54}=\frac{2}{27}$，属于等可能事件。
综上所述，只有C选项中的两个事件不是等可能的。
【答案】：
C

2. 长江是中华民族的母亲河,长江流域孕育出藏羌文化、巴蜀文化、荆楚文化、吴越文化等区域文化。若从上述四种区域文化中随机选一种文化开展专题学习,则选中“吴越文化”的概率是(A)
A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{3}{4}$

答案： 【解析】：
本题考察的是概率的基本计算。在概率论中，如果一个试验有n种等可能的结果，而事件A包含其中的m种结果，则事件A发生的概率为$P(A) = \frac{m}{n}$。
从题目中我们知道，有四种区域文化：藏羌文化、巴蜀文化、荆楚文化、吴越文化。因此，随机选一种文化，总共有4种等可能的结果。
而选中“吴越文化”是其中的1种结果。所以，选中“吴越文化”的概率是$\frac{1}{4}$。
【答案】：
A. $\frac{1}{4}$。

3. 在一个不透明的袋中,装有1个白球、2个红球、2个黄球、3个黑球,它们除颜色外都相同,搅匀后从袋中任意摸出1个球,可能性最大的是(D)
A.白球
B.红球
C.黄球
D.黑球

答案： 【解析】：
本题考察的是等可能性事件中各种事件出现的概率计算。
在一个不透明的袋中，装有不同颜色的球，我们需要计算摸出每种颜色球的概率，并比较这些概率以确定哪种颜色的球被摸出的可能性最大。
首先，我们需要确定袋中每种颜色球的数量：白球1个，红球2个，黄球2个，黑球3个。
然后，我们计算总球数：1（白）+ 2（红）+ 2（黄）+ 3（黑）= 8。
接着，我们分别计算摸出每种颜色球的概率：
摸出白球的概率：$P(\text{白球}) = \frac{1}{8}$，
摸出红球的概率：$P(\text{红球}) = \frac{2}{8} = \frac{1}{4}$，
摸出黄球的概率：$P(\text{黄球}) = \frac{2}{8} = \frac{1}{4}$，
摸出黑球的概率：$P(\text{黑球}) = \frac{3}{8}$。
最后，我们比较这些概率，可以看出摸出黑球的概率最大，即$\frac{3}{8}$。
【答案】：
D. 黑球。

4. 把一副普通扑克牌中的数字2,3,4,5,6,7,8,9,10的9张牌洗均匀后正面向下放在桌面上,从中随机抽取一张,抽出的牌上的数恰为3的倍数的概率是$\frac{1}{3}$。

答案： 【解析】：
本题主要考察等可能性事件中概率的计算。
首先，我们需要确定总的可能事件数，即从9张牌中随机抽取一张的方式有9种。
接着，我们需要确定满足条件的事件数，即抽出的牌上的数字是3的倍数的牌有哪些。
通过观察，我们可以发现数字3、6、9是3的倍数，因此满足条件的事件有3种。
最后，根据概率的定义，概率等于满足条件的事件数除以总的可能事件数，即$\frac{3}{9}$。
【答案】：
$\frac{1}{3}$

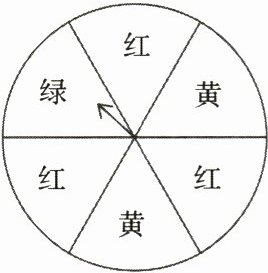
5. 如图是一个可以自由转动的转盘,转盘分成6个大小相同的扇形,颜色分为红、绿、黄三种颜色。指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形)。转动一次转盘后,指针指向______绿颜色的可能性最小。

答案： 【解析】：
本题考查等可能事件概率大小的计算。
需要先确定每种颜色扇形的数量，再根据数量判断指针指向哪种颜色的可能性最小。
观察转盘可知，转盘被分成$6$个大小相同的扇形，其中红色扇形有$3$个，绿色扇形有$1$个，黄色扇形有$2$个。
根据等可能事件概率的计算方法，在等可能事件中，某一事件发生的概率等于该事件包含的基本事件数除以总的基本事件数。
那么指针指向某种颜色扇形的概率就等于该颜色扇形的数量除以扇形的总数量。
扇形总数量为$6$个，红色扇形数量为$3$个，所以指针指向红色的概率为$\frac{3}{6}=\frac{1}{2}$；
绿色扇形数量为$1$个，所以指针指向绿色的概率为$\frac{1}{6}$；
黄色扇形数量为$2$个，所以指针指向黄色的概率为$\frac{2}{6}=\frac{1}{3}$。
比较$\frac{1}{2}$，$\frac{1}{6}$，$\frac{1}{3}$的大小，分母不同先通分，$2$、$6$、$3$的最小公倍数是$6$，则$\frac{1}{2}=\frac{3}{6}$，$\frac{1}{3}=\frac{2}{6}$。
因为$\frac{1}{6}＜\frac{2}{6}＜\frac{3}{6}$，即$\frac{1}{6}＜\frac{1}{3}＜\frac{1}{2}$，所以指针指向绿色的可能性最小。
【答案】：
绿

6. 甲袋中有红球8个、白球5个和黑球12个；乙袋中有红球27个、白球35个和黑球16个。
(1)如果你想取出1个黑球,选哪个袋子成功的机会大？请说明理由；
(2)如果你想取出1个红球,选哪个袋子成功的机会大？请说明理由；
(3)“从乙袋中取出红球10个后,乙袋中的红球个数仍比甲袋中红球个数多,所以此时若想取出1个红球,选乙袋成功的机会大”。你认为这种说法正确吗？为什么？

答案： 【解析】：
本题主要考察的是概率的计算，即某一事件发生的可能性大小。
(1)对于取出黑球的概率，我们需要比较两个袋子中黑球的比例。甲袋中黑球的比例是$\frac{12}{8+5+12}$，乙袋中黑球的比例是$\frac{16}{27+35+16}$。通过计算，我们可以比较这两个比例来确定在哪个袋子取出黑球的机会更大。
(2)对于取出红球的概率，我们同样需要比较两个袋子中红球的比例。甲袋中红球的比例是$\frac{8}{8+5+12}$，乙袋中红球的比例是$\frac{27}{27+35+16}$。通过计算，我们可以确定在哪个袋子取出红球的机会更大。
(3)对于第三问，我们需要先理解题目中的条件，然后重新计算乙袋中红球的比例，再与甲袋中红球的比例进行比较。注意，此时乙袋中红球的数量已经变为$27-10=17$。
【答案】：
(1)解：
甲袋中取出黑球的概率：
$P_{甲}(黑球) = \frac{12}{8+5+12} = \frac{12}{25}$
乙袋中取出黑球的概率：
$P_{乙}(黑球) = \frac{16}{27+35+16} = \frac{16}{78} = \frac{8}{39}$
因为 $\frac{12}{25} ＞ \frac{8}{39}$，所以选甲袋成功的机会大。
(2)解：
甲袋中取出红球的概率：
$P_{甲}(红球) = \frac{8}{8+5+12} = \frac{8}{25}$
乙袋中取出红球的概率：
$P_{乙}(红球) = \frac{27}{27+35+16} = \frac{27}{78} = \frac{9}{26}$
因为 $\frac{9}{26} ＞ \frac{8}{25}$，所以选乙袋成功的机会大。
(3)解：
乙袋中取出10个红球后，乙袋中红球的数量变为$27-10=17$，此时乙袋中取出红球的概率：
$P_{乙}'(红球) = \frac{17}{17+35+16} = \frac{17}{68} = \frac{1}{4}$
因为 $\frac{1}{4} ＜ \frac{8}{25}$（即甲袋中取出红球的概率），所以此时若想取出1个红球，选甲袋成功的机会大。故原说法不正确。