《2025年创新课时作业本九年级数学上册苏州专版》

1. 如图,在$Rt△ABC$中,$∠C= 90^{\circ },AC= 11cm$,点P从点A出发沿AC以1cm/s的速度移动,点Q从点C出发沿CB以2cm/s的速度移动,如果P、Q分别从A、C两点同时出发,当它们相距10cm时所需的时间为 (D)
A.3s
B.4s
C.5s
D.3s或1.4s

答案： 【解析】：本题可通过设未知数，根据勾股定理列出方程，进而求解得到时间。
设运动时间为$t$秒，因为点$P$从点$A$出发沿$AC$以$1cm/s$的速度移动，点$Q$从点$C$出发沿$CB$以$2cm/s$的速度移动，所以$AP = t cm$，$CQ = 2t cm$。
已知$AC = 11cm$，则$CP=(11 - t)cm$。
在$Rt\triangle PCQ$中，根据勾股定理$PQ^{2}=CP^{2}+CQ^{2}$，已知$PQ = 10cm$，可列出方程$(11 - t)^{2}+(2t)^{2}=10^{2}$，展开并化简该方程求解$t$的值。
【答案】：
解：设运动时间为$t$秒，则$AP = t cm$，$CQ = 2t cm$，$CP=(11 - t)cm$。
在$Rt\triangle PCQ$中，根据勾股定理可得：
$(11 - t)^{2}+(2t)^{2}=10^{2}$
$121 - 22t + t^{2}+4t^{2}=100$
$5t^{2}-22t + 121 - 100 = 0$
$5t^{2}-22t + 21 = 0$
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$，这里$a = 5$，$b = -22$，$c = 21$，
根据求根公式$t=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$可得：
$t=\frac{22\pm\sqrt{(-22)^{2}-4×5×21}}{2×5}=\frac{22\pm\sqrt{484 - 420}}{10}=\frac{22\pm\sqrt{64}}{10}=\frac{22\pm8}{10}$
解得$t_1=\frac{22 + 8}{10}=3$，$t_2=\frac{22 - 8}{10}=1.4$。
所以当它们相距$10cm$时所需的时间为$3s$或$1.4s$，答案选D。

2. 如图,在$Rt△ABC$中,$∠ABC= 90^{\circ },AB= 6cm,BC= 8cm$,动点P从点A出发沿边AB以1cm/s的速度向点B匀速移动,同时,点Q从点B出发沿边BC以2cm/s的速度向点C匀速移动,当P、Q两点中有一个点到达终点时另一个点也停止运动.运动多少秒后,$△PBQ面积为5cm^{2}$? (B)
A.0.5
B.1
C.5
D.1或5

答案： 【解析】：本题可根据三角形面积公式列出关于运动时间的方程，然后求解方程得到运动时间。
步骤一：设运动时间为$t$秒
已知动点$P$从点$A$出发沿边$AB$以$1cm/s$的速度向点$B$匀速移动，点$Q$从点$B$出发沿边$BC$以$2cm/s$的速度向点$C$匀速移动。
根据路程$=$速度$×$时间，可得$AP = t cm$，$BQ = 2t cm$。
步骤二：求出$PB$的长度
因为$AB = 6cm$，$AP = t cm$，所以$PB=(6 - t)cm$。
步骤三：根据三角形面积公式列出方程
已知$\angle ABC = 90^{\circ}$，所以$\triangle PBQ$是直角三角形，根据直角三角形面积公式$S=\frac{1}{2}×底×高$，可得${S}_{\triangle PBQ}=\frac{1}{2}× PB× BQ$。
已知${S}_{\triangle PBQ}=5cm^{2}$，$PB=(6 - t)cm$，$BQ = 2t cm$，代入面积公式可得：
$\frac{1}{2}×(6 - t)× 2t = 5$
步骤四：化简并求解方程
对$\frac{1}{2}×(6 - t)× 2t = 5$进行化简：
$(6 - t)× t = 5$
$6t - t^{2} = 5$
移项化为一元二次方程的一般形式：$t^{2} - 6t + 5 = 0$
因式分解得：$(t - 1)(t - 5) = 0$
则$t - 1 = 0$或$t - 5 = 0$，
解得$t_1 = 1$，$t_2 = 5$。
步骤五：检验$t$的值是否符合题意
已知$AB = 6cm$，$BC = 8cm$，点$P$的速度是$1cm/s$，点$Q$的速度是$2cm/s$。
点$P$从$A$到$B$所需时间为$6÷1 = 6s$，点$Q$从$B$到$C$所需时间为$8÷2 = 4s$。
因为当$P$、$Q$两点中有一个点到达终点时另一个点也停止运动，而$t = 5$时，点$Q$早已到达终点，所以$t = 5$不符合题意，舍去。
故$t = 1$，即运动$1$秒后，$\triangle PBQ$面积为$5cm^{2}$。
【答案】：B

3. 一个两位数,十位数字与个位数字之和为9,且这两个数字之积等于它们两个数字和的2倍,这个两位数是 (C)
A.36
B.63
C.36或63
D.-36或-63

答案： 【解析】：
本题主要考查一元二次方程的应用。
设这个两位数的十位数字为$x$，个位数字为$y$。
根据题意，我们可以列出以下两个方程：
十位数字与个位数字之和为9，即 $x + y = 9$。
这两个数字之积等于它们两个数字和的2倍，即 $xy = 2 × 9 = 18$。
接下来，我们解这个方程组：
从第一个方程，我们可以得到 $y = 9 - x$。
将这个表达式代入第二个方程，得到 $x(9 - x) = 18$。
展开并整理，得到 $9x - x^2 = 18$。
进一步整理，得到 $x^2 - 9x + 18 = 0$。
因式分解，得到 $(x - 3)(x - 6) = 0$。
解得 $x_1 = 3$，$x_2 = 6$。
当 $x = 3$ 时，$y = 9 - 3 = 6$。
当 $x = 6$ 时，$y = 9 - 6 = 3$。
因此，这个两位数可以是36或63。
【答案】：
C. $36$或$63$。

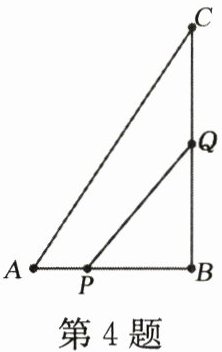
4. 如图,在$△ABC$中,$∠B= 90^{\circ },AB= 6,BC= 8$,点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,经过2或4秒,四边形APQC的面积等于$16cm^{2}$.

答案： 【解析】：本题可先根据$P$、$Q$的运动速度表示出$AP$、$BQ$的长度，进而得出$PB$的长度，然后根据三角形面积公式分别表示出$\triangle ABC$和$\triangle PBQ$的面积，最后根据四边形$APQC$的面积等于$\triangle ABC$的面积减去$\triangle PBQ$的面积列出方程求解。
步骤一：求出$\triangle ABC$的面积
在$\triangle ABC$中，$\angle B = 90^{\circ}$，$AB = 6cm$，$BC = 8cm$，根据直角三角形面积公式$S=\frac{1}{2}ab$（其中$a$、$b$为直角边），可得$\triangle ABC$的面积为：
$S_{\triangle ABC}=\frac{1}{2}× AB× BC=\frac{1}{2}× 6× 8 = 24cm^{2}$
步骤二：设运动时间为$t$秒，分别表示出$AP$、$BQ$、$PB$的长度
已知点$P$从点$A$开始沿边$AB$向点$B$以$1cm/s$的速度移动，点$Q$从点$B$开始沿边$BC$向点$C$以$2cm/s$的速度移动，根据路程$=$速度$×$时间，可得：
$AP = t cm$，$BQ = 2t cm$。
因为$AB = 6cm$，所以$PB=(6 - t)cm$。
步骤三：求出$\triangle PBQ$的面积
在$\triangle PBQ$中，$\angle B = 90^{\circ}$，$PB=(6 - t)cm$，$BQ = 2t cm$，根据直角三角形面积公式可得$\triangle PBQ$的面积为：
$S_{\triangle PBQ}=\frac{1}{2}× PB× BQ=\frac{1}{2}×(6 - t)× 2t=(6t - t^{2})cm^{2}$
步骤四：根据四边形$APQC$的面积列出方程并求解
因为四边形$APQC$的面积等于$\triangle ABC$的面积减去$\triangle PBQ$的面积，且四边形$APQC$的面积等于$16cm^{2}$，所以可列出方程：
$24 - (6t - t^{2}) = 16$
去括号得：$24 - 6t + t^{2} = 16$
移项化为一元二次方程的一般形式为：$t^{2} - 6t + 8 = 0$
因式分解得：$(t - 2)(t - 4) = 0$
则$t - 2 = 0$或$t - 4 = 0$，
解得$t_{1} = 2$，$t_{2} = 4$。
当$t = 4$时，$BQ = 2× 4 = 8cm$，此时$Q$点刚好运动到$C$点，符合题意；
当$t = 2$时，$BQ = 2× 2 = 4cm$，$P$、$Q$都在相应边上运动，也符合题意。
【答案】：$2$或$4$

5. 如图,A、B、C、D是矩形的四个顶点,$AB= 16cm,BC= 6cm$,动点P从点A出发,以3cm/s的速度向点B运动,直到点B为止;动点Q同时从点C出发,以2cm/s的速度向点D运动,当时间为1.6s或4.8s时,点P和点Q之间的距离是10cm.

答案： 【解析】：本题可通过设未知数，根据矩形的性质和勾股定理列出方程，进而求解得到时间。
设运动时间为$t$秒。
步骤一：分别表示出$AP$、$CQ$、$BP$、$DQ$的长度
已知动点$P$从点$A$出发，速度是$3cm/s$，根据路程$=$速度$×$时间，可得$AP = 3t cm$。
因为$AB = 16cm$，所以$BP=(16 - 3t)cm$。
动点$Q$从点$C$出发，速度是$2cm/s$，则$CQ = 2t cm$，又因为$CD = AB = 16cm$，所以$DQ=(16 - 2t)cm$。
步骤二：过点$Q$作$QE\perp AB$于点$E$，构造直角三角形
由于四边形$ABCD$是矩形，所以$QE = BC = 6cm$，$EQ$与$DC$平行且相等，则$BE = CQ = 2t cm$，那么$PE=|16 - 3t - 2t|=(16 - 5t)cm$。
步骤三：在$Rt\triangle PEQ$中，根据勾股定理列出方程
已知点$P$和点$Q$之间的距离是$10cm$，即$PQ = 10cm$，在$Rt\triangle PEQ$中，由勾股定理$a^2 + b^2 = c^2$（其中$a$、$b$为直角边，$c$为斜边）可得：
$PE^{2}+QE^{2}=PQ^{2}$，即$(16 - 5t)^{2}+6^{2}=10^{2}$。
步骤四：解方程
对$(16 - 5t)^{2}+6^{2}=10^{2}$进行求解：
$\begin{aligned}(16 - 5t)^{2}+36&=100\\(16 - 5t)^{2}&=100 - 36\\(16 - 5t)^{2}&=64\\16 - 5t&=\pm8\end{aligned}$
当$16 - 5t = 8$时，
$5t = 16 - 8$，
$5t = 8$，
解得$t=\frac{8}{5}=1.6$。
当$16 - 5t = -8$时，
$5t = 16 + 8$，
$5t = 24$，
解得$t = \frac{24}{5}=4.8$。
因为$P$点从$A$到$B$运动，$AP = 3t\leqslant16$，即$t\leqslant\frac{16}{3}$；$Q$点从$C$到$D$运动，$CQ = 2t\leqslant16$，即$t\leqslant8$，$1.6$和$4.8$都满足条件。
【答案】：$1.6s$或$4.8s$

6. 如图,在$△ABC$中,$∠C= 90^{\circ },AC= 16cm,BC= 8cm$,一动点P从点C出发沿着CB方向以2cm/s的速度运动,另一动点Q从点A出发沿着边AC以4cm/s的速度运动,P、Q两点同时出发,运动时间为t(单位:s).
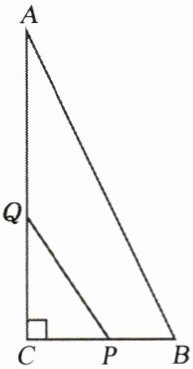
(1) 若$△PCQ的面积是△ABC面积的\frac {1}{4}$,求t的值;
(2)$△PCQ$的面积能否与四边形ABPQ面积相等? 若能,求出t的值;若不能,说明理由.

答案： 【解析】：本题主要考查一元二次方程的应用，通过三角形面积公式建立方程来求解。
（1）首先，根据$S=\frac{1}{2}ah$（a为底，h为高），可得$\bigtriangleup ABC$的面积为：$S_{\bigtriangleup ABC}=\frac{1}{2}× AC× BC$。
已知$AC = 16cm$，$BC = 8cm$，则$S_{\bigtriangleup ABC}=\frac{1}{2}×16×8 = 64cm^{2}$。
因为点P的速度是$2cm/s$，运动时间为t，所以$PC = 2t cm$；点Q的速度是$4cm/s$，运动时间为t，所以$CQ=(16 - 4t)cm$。
那么$\bigtriangleup PCQ$的面积为：$S_{\bigtriangleup PCQ}=\frac{1}{2}× PC× CQ=\frac{1}{2}× 2t×(16 - 4t)=(16t - 4t^{2})cm^{2}$。
已知$\bigtriangleup PCQ$的面积是$\bigtriangleup ABC$面积的$\frac{1}{4}$，则可列出方程：
$16t - 4t^{2}=\frac{1}{4}×64$。
化简方程得：$16t - 4t^{2}=16$，移项化为标准的一元二次方程形式：$4t^{2}-16t + 16 = 0$，两边同时除以4得：$t^{2}-4t + 4 = 0$。
由完全平方公式$(a-b)^2=a^2-2ab+b^2$，可得$(t - 2)^{2}=0$，解得$t_{1}=t_{2}=2$。
所以，t的值为2。
（2）四边形$ABPQ$的面积$S_{四边形ABPQ}=S_{\bigtriangleup ABC}-S_{\bigtriangleup PCQ}$。
若$\bigtriangleup PCQ$的面积与四边形$ABPQ$面积相等，则$S_{\bigtriangleup PCQ}=\frac{1}{2}S_{\bigtriangleup ABC}$。
即$16t - 4t^{2}=\frac{1}{2}×64$，化简方程得：$16t - 4t^{2}=32$，移项化为标准的一元二次方程形式：$4t^{2}-16t + 32 = 0$，两边同时除以4得：$t^{2}-4t + 8 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$，其判别式$\Delta=b^{2}-4ac$，在方程$t^{2}-4t + 8 = 0$中，$a = 1$，$b = - 4$，$c = 8$，则$\Delta=(-4)^{2}-4×1×8=16 - 32=-16\lt0$。
当$\Delta\lt0$时，一元二次方程无实数解。
所以，$\bigtriangleup PCQ$的面积不能与四边形$ABPQ$面积相等。
【答案】：
(1)$t = 2$；
(2)不能，理由：由上述计算可知，对应的一元二次方程无实数解。