《2025年畅行课堂七年级数学下册华师大版》

1. 多边形的外角和等于（ ）
A. $180^{\circ}$
B. $360^{\circ}$
C. $540^{\circ}$
D. $720^{\circ}$

答案： B

2.（襄阳中考）正五边形的外角和为（ ）
A. $180^{\circ}$
B. $360^{\circ}$
C. $540^{\circ}$
D. $720^{\circ}$

答案： B

3.（2024·济南）若正多边形的一个外角是$45^{\circ}$，则这个正多边形是（ ）
A. 正六边形
B. 正七边形
C. 正八边形
D. 正九边形

答案： C

4. 若某多边形的边数增加1，则这个多边形的外角和（ ）
A. 增加$180^{\circ}$
B. 增加$360^{\circ}$
C. 减少$180^{\circ}$
D. 不变

答案： D

5.（2024·遂宁）佩佩在“黄娥古镇”研学时学习扎染技术，得到一个内角和为$1080^{\circ}$的正多边形图案，这个正多边形的每个外角为（ ）
A. $36^{\circ}$
B. $40^{\circ}$
C. $45^{\circ}$
D. $60^{\circ}$

答案： C

6. 已知一个多边形的每一个外角都等于$18^{\circ}$，下列说法错误的是（ ）
A. 这个多边形是二十边形
B. 这个多边形的内角和是$3600^{\circ}$
C. 这个多边形的每个内角都是$162^{\circ}$
D. 这个多边形的外角和是$360^{\circ}$

答案： B

7. 如图，在五边形$ABCDE$中，$\angle BAE = 110^{\circ}$，则$\angle 1+\angle 2+\angle 3+\angle 4=$_______.

答案： $290^{\circ}$

8.（2024·宁乡市月考）一个多边形的内角和是$1080^{\circ}$.
（1）求该多边形的边数；
（2）若该多边形每个内角都相等，求每一个外角的度数.

答案： 解：
(1)设该多边形的边数为$n$.
$\therefore(n - 2)\times180^{\circ}=1080^{\circ}$，$\therefore n = 8$，
$\therefore$边数为8.
(2)$\because$该多边形每个内角都相等，由于等角的补角相等，故该多边形每个外角都相等，
$\therefore$每一个外角的度数$=\frac{360^{\circ}}{8}=45^{\circ}$.

9.（2024·惠城区期中）如图，$\angle A+\angle B+\angle C+\angle D+\angle DEC+\angle AFB$等于（ ）


A. $360^{\circ}$
B. $720^{\circ}$
C. $180^{\circ}$
D. $540^{\circ}$

答案： A

10. 如图，在正六边形$ABCDEF$内，以$AB$为边作正五边形$ABGHI$，则$\angle FAI=$_______.

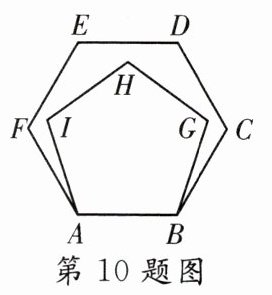
答案： $12^{\circ}$

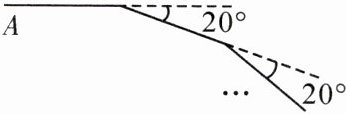
11. 如图，小明从点$A$出发，前进$10\ m$后向右转$20^{\circ}$，再前进$10\ m$后又向右转$20^{\circ}$，这样一直下去，直到他第一次回到出发点$A$为止，他所走的路径构成了一个多边形.
（1）小明一共走了多少米？
（2）这个多边形的内角和是多少度？

答案： 解：
(1)根据题意可知，所经过的路线正好构成一个外角是$20^{\circ}$的正多边形，
$\therefore360\div20 = 18$，$18\times10 = 180$（m）.
答：小明一共走了180 m.
(2)$(18 - 2)\times180^{\circ}=2880^{\circ}$.
答：这个多边形的内角和是$2880^{\circ}$.