《2025年课堂点睛七年级数学上册北师大版》

11. 过一个多边形的一个顶点的所有对角线把多边形分成 4 个三角形,则这个多边形的边数为(D)
A.3
B.4
C.5
D.6

答案： D

12. 若从一个多边形的一个顶点出发,最多可画 2024 条对角线,则它是2027边形.

答案： 2027

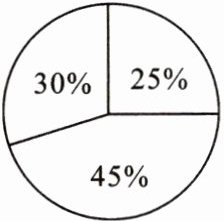
13. 如图,把一个圆分成三个扇形,若圆的半径为 2,则最小扇形的圆心角度数为90°；最大扇形的面积为$\frac{9\pi}{5}$.
]

答案： 90° $\frac{9\pi}{5}$

14. 已知 A、B、C 是同一直线上的三点,点 D 为 AB 的中点,若 AB = 12,BC = 7,则 CD 的长为(C)
A.1
B.13
C.13 或 1
D.9.5

答案： C

15. 将一个正六边形纸片对折,并完全重合,那么得到的图形是四或五边形.

答案： 四或五

16. 已知∠AOB = 80°,∠BOC = 50°,OD 是∠AOB 的角平分线,OE 是∠BOC 的角平分线,则∠DOE = 65°或15°.

答案： 65°或15°

17. 已知点 C 在线段 AB 上,且 AC = 6,BC = 4,M,N 分别是 AC,BC 的中点.
(1) 求线段 MN 的长度；
(2) 如果 AC = a,BC = b,其他条件不变,你能猜出 MN 的长度吗？
(3) 如果我们这样叙述它：“已知点 C 与线段 AB 在同一直线上,线段 AC = 6,BC = 4,M,N 分别是 AC,BC 的中点,求 MN 的长度.”结果会有变化吗？如果有,求出结果.

答案：

(1)解：
∵AC=6，BC=4，点M，N分别是AC，BC的中点，
∴MN=$\frac{1}{2}$(AC+CB)=$\frac{1}{2}$×10=5；
(2)MN=$\frac{a+b}{2}$，直线上相邻两线段中点间的距离为两线段长度和的一半；
(3)如图:，有变化，会出现两种情况：①当点C在线段AB上时，MN=$\frac{1}{2}$(AC+BC)=5；②当点C在AB的延长线上时，MN=$\frac{1}{2}$(AC-BC)=1.

18. 如图所示,已知在同一平面内∠AOB = 90°,∠AOC = 60°.

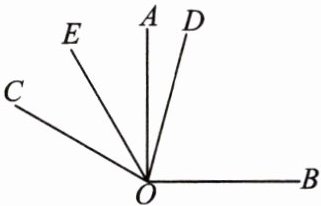
(1) 计算：∠BOC = 150°.
(2) 若 OD 平分∠BOC,OE 平分∠AOC,直接写出∠DOE 的度数为45°.
(3) 试问在(2)的条件下,如果将题目中∠AOC = 60°改成∠AOC = 2α(α ＜ 45°),其他条件不变,你能求出∠DOE 的度数吗？若能,请你写出求解过程；若不能,请说明理由.
能.理由：因为∠AOB=90°，∠AOC=2α，所以∠BOC=90°+2α.因为OD，OE分别平分∠BOC，∠AOC，所以∠DOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(90°+2α)=45°+α，∠COE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×2α=α，所以∠DOE=∠DOC-∠COE=45°+α-α=45°.

答案：
(1)150°
(2)45°
(3)解：能.理由：因为∠AOB=90°，∠AOC=2α，所以∠BOC=90°+2α.因为OD，OE分别平分∠BOC，∠AOC，所以∠DOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(90°+2α)=45°+α，∠COE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×2α=α，所以∠DOE=∠DOC-∠COE=45°+α-α=45°.