《2025年课堂点睛七年级数学上册北师大版》

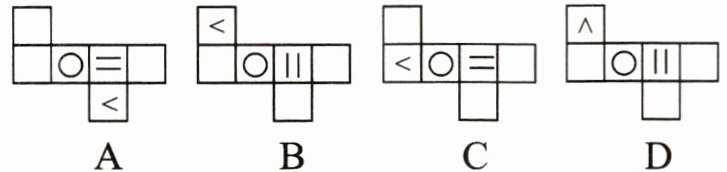
7. 将如图所示的正方体沿某些棱展开后,能得到的图形是 (B)

答案： B

8. (威海市中考)如图是一正方体的表面展开图. 将其折叠成正方体后,与顶点K距离最远的顶点是 (D)

A.A点
B.B点
C.C点
D.D点

答案： D

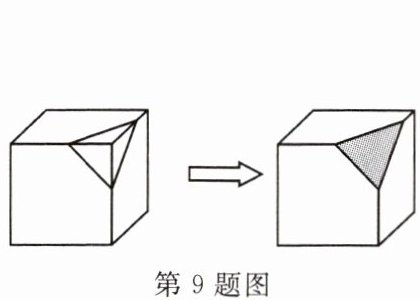
9. 如图,将图中的正方体纸盒切去一角得到右图,下列选项中,不能作为纸盒剩余部分的展开图的是 (C)

答案： C

10. 某综合实践小组进行废物再利用的环保小卫士行动. 他们准备用废弃的宣传单制作装垃圾的无盖纸盒. 操作探究如下：


(1)若准备制作一个无盖的正方体纸盒,图1中的C图形经过折叠能围成无盖正方体纸盒.
(2)图2是小明的设计图,把它折成无盖正方体纸盒后,与“小”字相对的字是环.

答案：
(1)C　
(2)环

11. (核心素养·空间观念)如图①所示,从大正方体中截去一个小正方体之后,可以得到图②的几何体.

(1)设原大正方体的表面积为a,图②中几何体的表面积为b,那么a与b的大小关系是____；(填序号)
A. $ a ＞ b $
B. $ a ＜ b $
C. $ a = b $
D. 无法判断
(2)小明说“设图①中大正方体的棱长之和为m,图②中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗？为什么？
(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图③是图②几何体的表面展开图吗？如有错误,请予修正.

答案：

(1)C　
(2)解:如图④标粗的棱是多出来的，共6条，如果截去的小正方体的棱长为大正方体的棱长的一半时,n比m正好多出大正方体的3条棱的长度;如果截去的小正方体的棱长不是大正方体的棱长的一半时,n比m就不是多出大正方体的3条棱的长度.故小明的说法是不正确的.　　　　　　　　 　　
(3)图③不是图②几何体的表面展开图，改后的图形,如图⑤所示.