第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 两点之间的所有连线中,
线段最短
。
答案:
线段最短
2. 两点之间______,叫作这两点之间的距离。
答案:
线段的长度
3. 把一条线段分成相等的两条线段的点叫线段的
中点
。
答案:
中点
如图,点C为线段AB的中点,点D为线段BC的中点,AB= 4cm,求线段AD的长度。

【自主解答】
解:∵AB= 4cm,C是AB中点,
∴AC= BC= $\frac{1}{2}$AB= 2(cm),
∵D是BC中点,
∴CD= $\frac{1}{2}$BC= 1(cm),
∴AD= AC+CD= 3cm。
【方法归纳】本题考查了线段的和差、线段的中点等知识。先根据线段中点的性质求出AC、BC、CD的长,再根据线段的和差关系求解即可。

【自主解答】
解:∵AB= 4cm,C是AB中点,
∴AC= BC= $\frac{1}{2}$AB= 2(cm),
∵D是BC中点,
∴CD= $\frac{1}{2}$BC= 1(cm),
∴AD= AC+CD= 3cm。
【方法归纳】本题考查了线段的和差、线段的中点等知识。先根据线段中点的性质求出AC、BC、CD的长,再根据线段的和差关系求解即可。
答案:
【自主解答】
解:
∵AB= 4cm,C是AB中点,
∴AC= BC= $\frac{1}{2}$AB= 2(cm),
∵D是BC中点,
∴CD= $\frac{1}{2}$BC= 1(cm),
∴AD= AC+CD= 3cm。
【方法归纳】本题考查了线段的和差、线段的中点等知识。先根据线段中点的性质求出AC、BC、CD的长,再根据线段的和差关系求解即可。
解:
∵AB= 4cm,C是AB中点,
∴AC= BC= $\frac{1}{2}$AB= 2(cm),
∵D是BC中点,
∴CD= $\frac{1}{2}$BC= 1(cm),
∴AD= AC+CD= 3cm。
【方法归纳】本题考查了线段的和差、线段的中点等知识。先根据线段中点的性质求出AC、BC、CD的长,再根据线段的和差关系求解即可。
1. (柳州市中考)如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是(
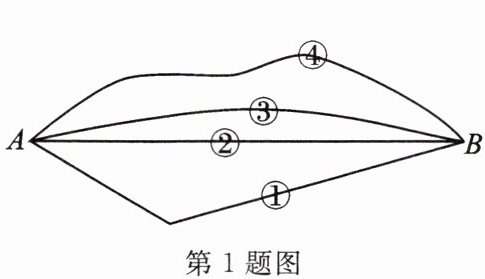
A.①
B.②
C.③
D.④
B
)
A.①
B.②
C.③
D.④
答案:
B
2. 下列说法中正确的有(
①过两点有且只有一条直线;②连接两点的线段叫两点之间的距离;③两点之间线段最短;④直线比射线长。
A.1个
B.2个
C.3个
D.4个
B
)①过两点有且只有一条直线;②连接两点的线段叫两点之间的距离;③两点之间线段最短;④直线比射线长。
A.1个
B.2个
C.3个
D.4个
答案:
B
3. 把弯曲的河道改直,能够缩短航程,这样做根据的道理是
两点之间线段最短
。
答案:
两点之间线段最短
4. 体育课上,小明在点O处进行了四次铅球试投,铅球分别落在图中的M,N,P,Q四个点处,则表示他最好成绩的点是(
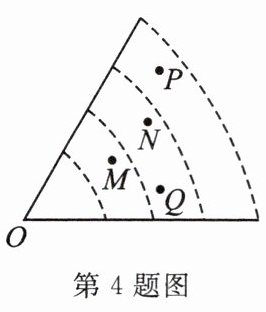
A.M
B.N
C.P
D.Q
C
)
A.M
B.N
C.P
D.Q
答案:
C
5. 如图,用一支角度固定的圆规比较线段a,b的长短,则(
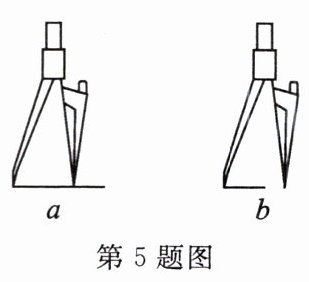
A.a>b
B.a= b
C.a<b
D.无法确定
A
)
A.a>b
B.a= b
C.a<b
D.无法确定
答案:
A
6. (教材第117页习题第4题变式)尺规作图,不写作法,必须保留作图痕迹。已知线段a和b,求作:线段c= 2b-a。


答案:
解:如图 ,作射线OM,在射线OM上截取OA=AB=b,BC=a,则线段OC=2b−a.即线段OC即为所求.
,作射线OM,在射线OM上截取OA=AB=b,BC=a,则线段OC=2b−a.即线段OC即为所求.
解:如图
 ,作射线OM,在射线OM上截取OA=AB=b,BC=a,则线段OC=2b−a.即线段OC即为所求.
,作射线OM,在射线OM上截取OA=AB=b,BC=a,则线段OC=2b−a.即线段OC即为所求. 7. 下列说法正确的是(
A.若AB= 2AD,则点D为线段AB的中点
B.若AD= $\frac{1}{2}$AB,则点D为线段AB的中点
C.若点D为线段AB的中点,则AD= BD
D.若点D为线段AB的中点,则AD= 2BD
C
)A.若AB= 2AD,则点D为线段AB的中点
B.若AD= $\frac{1}{2}$AB,则点D为线段AB的中点
C.若点D为线段AB的中点,则AD= BD
D.若点D为线段AB的中点,则AD= 2BD
答案:
C
查看更多完整答案,请扫码查看


