《2025年课堂点睛七年级数学上册北师大版》

1. 有一个游戏的规则是：你想一个数,乘以 2,加上 6,再除以 2,最后减去你所想的数,我就知道结果. 这个结果是(C)
A.1
B.2
C.3
D.4

答案： C

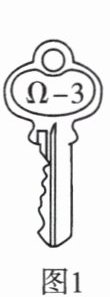
2. (跨学科)为了保密,许多情况下需要采用密码,破译密码有一把“钥匙”. 如图 1,密码“钥匙”显示 $\Omega - 3$,表示将密文中每个字母在图 2 中沿逆时针方向转动 3 位. 例如,破译 kdssb 得 happy. 继续使用此密码“钥匙”,破译 pdwkv 得maths.
]

答案： maths

3. 一个两位数,其中 $a$ 表示十位上的数字,$b$ 表示个位上的数字($a eq b$,$ab eq 0$),把十位、个位上的数字互换位置得到一个新两位数,则这两个两位数的和一定能被数11整除,这两个两位数的差一定能被数9整除.

答案： 11 9

4. (教材第 98 页随堂练习变式)有三堆棋子,数目相等,每堆至少有 5 枚,从左堆中取出 4 枚放入中堆,从右堆中取出 5 枚放入中堆,再从中堆中取出与左堆剩余棋子数相同的棋子数放入左堆,这时中堆的棋子数是13 枚.

答案： 13 枚

5. 陈老师和学生做一个猜数游戏,他让学生按照如下步骤进行计算：
①任想一个两位数 $a$,把 $a$ 乘以 2,再加上 9,把所得的和再乘以 2；
②把 $a$ 乘以 2,再加上 30,把所得的和除以 2；
③把①所得的结果减去②所得的结果,这个差即为最后的结果.
陈老师说：只要你告诉我最后的结果,我就能猜出你最初想的两位数 $a$. 学生周晓晓计算的结果是 96,陈老师立即猜出周晓晓最初想的两位数是 31.
请用自己的语言解释陈老师是怎样算出来的？

答案： 解:由题意可得,①的结果为$(2a+9)×2=4a+18$,②的结果为$(2a+30)÷2=a+15$;③的结果为$(4a+18)-(a+15)=3a+3$;令$3a+3=96$,解得$a=31$.

6. 小明和小红玩猜数字游戏,小明说：“你随便在自然数中选定三个一位数,按下列步骤进行计算：①把第一个数乘以 2,②加上 5,③把所得的和乘以 5,④加上第二个数字,⑤再把所得的和乘以 10,⑥再加上第三个数字,只要你告诉我最后的得数,我就知道你所选的三个一位数.”若小红告诉小明最后得到的结果是 846,则小红所报的第 2 个数是9.

答案： 9

7. 【阅读理解】计算：$25×11 = 275$,$13×11 = 143$,$48×11 = 528$,$74×11 = 814$,观察算式,我们发现两位数乘 11 的速算方法：头尾一拉,中间相加,满十进一.
【拓展应用】已知一个两位数,十位上的数字是 $a$,个位上的数字是 $b$,这个两位数乘 11,计算结果的十位上的数字可表示为(D)
A.$a$ 或 $a + 1$
B.$a + b$ 或 $ab$
C.$a + b - 10$
D.$a + b$ 或 $a + b - 10$

答案： D