《2025年课堂点睛七年级数学上册北师大版》

7. 已知$\angle AOB = 70^{\circ}$,$\angle AOC = 30^{\circ}$,则$\angle COB = $40°或 100°。

答案： 40°或 100°

8. (湖北省中考改编)如图所示,$C$,$O$,$D$三点共线,$\angle AOC = 40^{\circ}$,$\angle BOD = 50^{\circ}$,$OM$,$ON分别是\angle AOC$,$\angle BOD$的平分线,则$\angle MON$等于(D)

A.$45^{\circ}$
B.$90^{\circ}$
C.$165^{\circ}$
D.$135^{\circ}$

答案： D

9. 如图,是一副特殊的三角板,用它们可以画出一些特殊角,不能利用这副三角板画出的角度是(D)

A.$135^{\circ}$
B.$162^{\circ}$
C.$81^{\circ}$
D.$30^{\circ}$

答案： D

10. 如图所示,将两块直角三角板的直角顶点重合,若$\angle AOD = 144^{\circ}42'$,则$\angle BOC = $35.3$^{\circ}$。

答案： 35.3

11. 如图所示,$\angle AOB$是平角,$\angle BOC = 36^{\circ}$,$OD平分\angle AOC$,$\angle DOE = 90^{\circ}$,求$\angle AOE$的度数。

答案： 解:
∵∠AOB 是平角,∠BOC=36°,
∴∠AOC=180°-∠BOC=180°-36°=144°,
∵OD 平分∠AOC,
∴∠AOD=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×144°=72°,
∵∠DOE=90°,
∴∠AOE=∠DOE-∠AOD=90°-72°=18°.

12. (一题多设问)
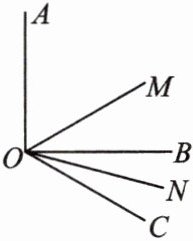
(1)如图,$\angle AOB = 90^{\circ}$,$\angle BOC = 30^{\circ}$,$OM平分\angle AOC$,$ON平分\angle BOC$。则$\angle MON$的度数为45°；
(2)如果(1)中$\angle AOB = \alpha$,其他条件不变,求$\angle MON$的度数；
(3)如果(1)中,$\angle BOC = \beta$($\beta$为锐角),其他条件不变,求$\angle MON$的度数；
(4)从(1)(2)(3)的结果中能看出什么规律？

答案：
(1)45°
(2)解:∠MON=∠MOC-∠NOC=$\frac{1}{2}$∠AOC-$\frac{1}{2}$∠BOC=$\frac{1}{2}$(α+30°)-$\frac{1}{2}$×30°=$\frac{1}{2}$α.
(3)∠MON=$\frac{1}{2}$∠AOC-$\frac{1}{2}$∠BOC=$\frac{1}{2}$(90°+β)-$\frac{1}{2}$β=$\frac{1}{2}$×90°=45°.
(4)∠MON=$\frac{1}{2}$∠AOB.

1. 将一张长方形纸片按如图所示的方式折叠,$BD$、$BE$为折痕,若$\angle ABE = 20^{\circ}$,则$\angle DBC$为70°。

答案： 70°

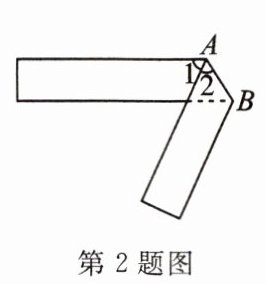
2. 如图,把一张长方形纸片沿$AB$折叠后,若$\angle 1 = 50^{\circ}$,则$\angle 2$的度数为65°。

答案： 65°

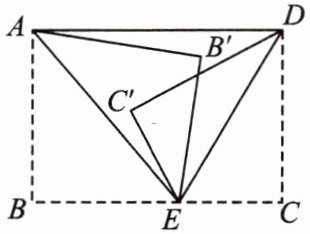
3. 如图,将长方形纸片$ABCD$按如图所示方式折叠,折叠后点$B落到B'$,点$C落到C'$,$AE$,$DE$为折痕,且$\angle B'EC' = 36^{\circ}$,则$\angle AEB + \angle DEC = $108$^{\circ}$。

答案： 108