《2025年课堂点睛七年级数学上册北师大版》

1. 用具体数值代替式中的字母,按照代数式中给出的运算,计算出的结果,叫作代数式的值。

答案： 代数式的值

2. 数值转换机的本质就是求____。

答案： 代数式的值

按如图的程序计算,若开始输入的$x值为2$,求最后输出的结果。

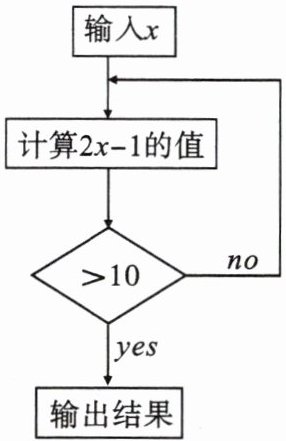
答案： 自主解答
解：当$x = 2$时,$2x - 1 = 2×2 - 1 = 3 ＜ 10$；
将$x = 3$代入得：$2x - 1 = 2×3 - 1 = 5 ＜ 10$；
将$x = 5$代入得：$2x - 1 = 2×5 - 1 = 9 ＜ 10$；
将$x = 9$代入得：$2x - 1 = 2×9 - 1 = 17 ＞ 10$。
故输出结果为$17$。
方法归纳本题主要考查了求代数式的值,有理数的混合运算,本题是操作型题目,由数值转换机的程序图得到代数式是解题的关键。

1. 当$x = -1$时,代数式$3x + 1$的值为(B)
A.$-1$
B.$-2$
C.$4$
D.$-4$

答案： B

2. 若$x = -3$,$y = 1$,则代数式$2x - 3y + 1$的值为(B)
A.$-10$
B.$-8$
C.$4$
D.$10$

答案： B

3. 若$x^{2} + 3x的值为7$,则$x^{2} + 3x - 2$的值为5。

答案： 5

4. 某市有一块长为$4$米,宽为$b$米的长方形地块,如图所示,规划部门计划将阴影部分绿化,中间正方形空地将修建一座雕像。
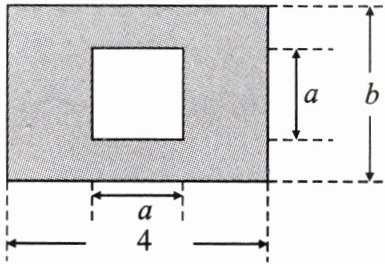
(1)试用含$a$,$b$的式子表示绿化的面积是多少平方米？
(2)若$a = 2$,$b = 3$,求出绿化面积。

答案：
(1)解:根据题意得$4b-a^{2}$.答:绿化的面积是$(4b-a^{2})$平方米.
(2)将$a=2,b=3$代入
(1)题结果得$4×3-2^{2}=8$(平方米),答:若$a=2,b=$3,绿化面积为8平方米.

5. 按如图所示的程序计算,若开始输入的数为$-2$,求最后输出的结果。

答案： 解:把-2 代入得$(-2)×3-(-2)=-6+2=-4$$＞-5$,再把-4 代入得$(-4)×3-(-2)=-12+2=-10＜-5$,即最后输出的结果是-10.

6. 已知等边三角形的边长为$p$,正方形的边长为$q$,则$3p + 4q$的实际意义为等边三角形的周长与正方形的周长之和。

答案： 等边三角形的周长与正方形的周长之和

7. 请你结合自身生活实际,设计具体情境,解释下列代数式的意义：
(1)$a^{3}$；
(2)$2a - b$。

答案：
(1)解:一个正方体盒子,其棱长为a cm,则它的体积为$a^{3}cm^{3}$(答案不唯一).
(2)甲有a个笔记本,乙的笔记本的个数是甲的2倍少b个,则乙的笔记本的个数可表示为$(2a-b)$个.(答案不唯一)