《2025年课堂点睛七年级数学上册北师大版》

9. (贵州省中考改编)我们从不同的方向观察同一物体时,可能看到不同的图形,则从正面、左面、上面观察都不可能看到长方形的是(C)

答案： C

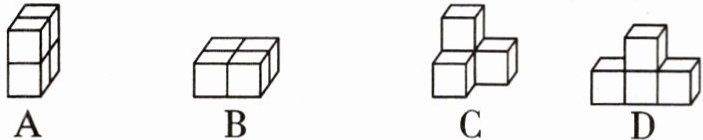
10. 用四个相同的小立方块搭几何体,要求从正面、左面、上面看到的几何体的形状图中至少有两个是相同的,则如图所示四种摆放方式中不符合要求的是(D)

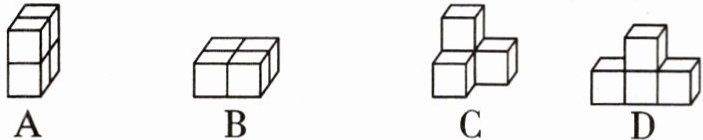
答案： D

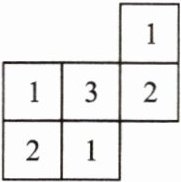
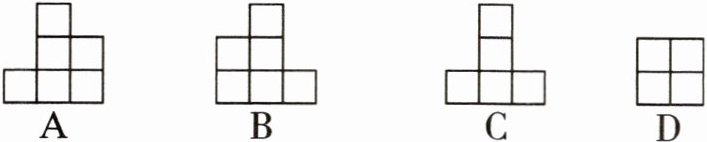
11. 如图是一个由多个相同小正方体堆积而成的几何体从上面看到的形状图,图中所示的数字为该位置小正方体的个数,则这个几何体从左面看到的形状图是(A)

答案： A

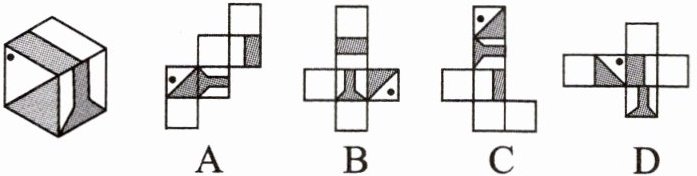
12. 如图所示的正方体的展开图是(D)

答案： D

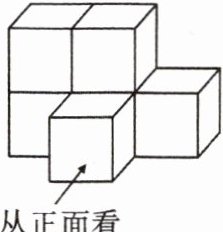
13. 如图是由 6 块完全相同的小正方体搭成的几何体,如果在这个几何体上再添加一些小正方体,并保持从正面和从左面看到的形状不变,则最多可以添加2块小正方体.

答案： 2

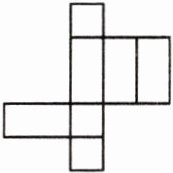
14. 小明用若干个正方形和长方形拼成了一个长方体的展开图,拼完后,小明看来看去觉得所拼图形(如图)似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题. 若有多余图形,请将多余部分涂上颜色；若图形不全,则直接在原图中补全；
(2)若图中的正方形边长为 5cm,长方形的长为 8cm,则修正后所折叠而成的长方体的表面积为$____cm^2.$

答案：

(1)解:拼图存在问题,多出一个正方形,如图所示.
(2)210

15. 一个几何体是由若干个棱长为 3cm 的小正方体搭成的,从左面、上面看到的几何体的形状图如图所示：

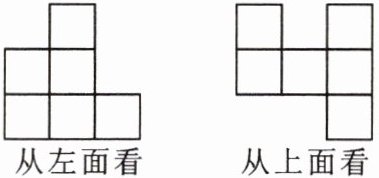
(1)该几何体最少由9个小正方体组成,最多由14个小正方体组成；
(2)将该几何体的形状固定好.
①求该几何体体积的最大值；
②若要给体积最小时的几何体表面涂上油漆,求所涂油漆面积的最小值.
(2)解:①$3^{3}× 14=378(cm^3)$. ②$9× (2× 6+2× 5+2× 7)=324(cm^2)$.

答案：
(1)9 14
(2)解:①$3^{3}× 14=378(cm^3)$. ②$9× (2× 6+2× 5+2× 7)=324(cm^2)$.