《2025年课堂点睛七年级数学上册北师大版》

8. (程序题)如图,当输入$a = -2$,$b = -3$时,输出的$y$的值为-7。

答案： -7

9. 已知$x - 2y + 2 = 0$,则代数式$(2y - x)^{2} - (x - 2y) - 1$的值为(A)
A.$5$
B.$14$
C.$13$
D.$7$

答案： A

10. 一批产品,甲单独做$a$小时可以完成,乙单独做$b$小时可以完成,现在已完成了任务的$\frac{2}{a} + \frac{5}{b}$,则甲、乙的工作情况是甲已工作了2小时,乙已工作了5小时。

答案： 甲已工作了2小时,乙已工作了5小时

11. 按如图的运算程序计算,若开始输入的$x值为24$,那么第一次输出的结果为$12$,…,则第$2024$次输出的结果为6。

答案： 6

12. (宁夏自治区中考)如图是某种杆秤的示意图。在秤杆的点$A$处固定提纽,点$B$处挂秤盘,点$C为0$刻度点。当秤盘不放物品时,提起提纽,秤砣所挂位置移动到点$C$,秤杆处于平衡。秤盘放入$x$克物品后移动秤砣,当秤砣所挂位置与提纽的距离为$y$毫米时秤杆处于平衡。测得$x与y$的几组对应数据如下表：


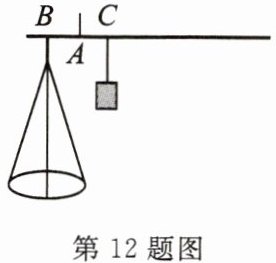
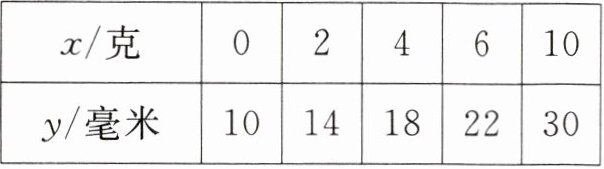
由表中数据的规律可知,当$x = 20$克时,$y = $50毫米。

答案： 50

13. (教材第$78$页例题变式)七年级学生在$5$名教师的带领下去公园秋游,公园的门票为每人$30$元,现有两种优惠方案,甲方案：带队教师免费,学生按八折收费：乙方案：师生都七五折收费。
(1)若有$m$名学生,用代数式表示两种优惠方案各需多少元？
(2)当$m = 70$时,采用哪种方案优惠？

答案：
(1)解:甲方案:$m×30×0.8=24m$(元),乙方案:$(m+5)×30×0.75=22.5(m+5)$(元).
(2)当$m=70$时,甲方案付费为$24×70=1680$(元),乙方案付费$22.5×75=1687.5$(元),因为$1680＜1687.5$,所以采用甲方案优惠.

14. (核心素养·运算能力)(1)按下表已填写的完成表中的空白处代数式的值：

(2)比较表中两代数式的计算结果,请写出$(a - b)^{2}与a^{2} - 2ab + b^{2}$之间有什么关系？
(3)利用你发现的结论,求$2024^{2} - 4048×2025 + 2025^{2}$。
(1)41699
(2)解:根据(1)中数据可得$(a-b)^{2}=a^{2}-2ab+b^{2}.$
(3)由(2)中的等式可知:$2024^{2}-4048×2025+2025^{2}=2024^{2}-2×2024×2025+2025^{2}=(2024-2025)^{2}=1.$

答案：
(1)4 16 9 9
(2)解:根据
(1)中数据可得$(a-b)^{2}=a^{2}-2ab+b^{2}$.
(3)由
(2)中的等式可知:$2024^{2}-4048×2025+2025^{2}=2024^{2}-2×2024×2025+2025^{2}=(2024-2025)^{2}=1.$