第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
1. 按一定规律排列的一组数据为$\frac{1}{2},-\frac{3}{5},\frac{1}{2},-\frac{7}{17},\frac{9}{26},-\frac{11}{37},…$,则第$10$个数是(
A.$-\frac{19}{101}$
B.$\frac{21}{101}$
C.$-\frac{19}{82}$
D.$\frac{21}{82}$
A
)。A.$-\frac{19}{101}$
B.$\frac{21}{101}$
C.$-\frac{19}{82}$
D.$\frac{21}{82}$
答案:
A
2. 按规律排列的一列单项式为$x,-x^{3},x^{5},-x^{7},x^{9},…$,则第$20$个单项式是
-x³⁹
。
答案:
-x³⁹
3. 苯是一种有机化合物,是组成结构最简单的芳香烃,可以合成一系列衍生物。某小组用小木棒摆放的苯及其衍生物的结构式如图所示,第$1个图形需要9$根小木棒,第$2个图形需要16$根小木棒,第$3个图形需要23$根小木棒……按此规律,第$n$个图形需要(
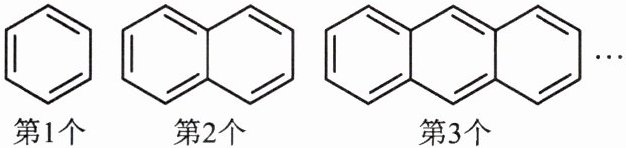
A.$(7n + 9)$根
B.$(7n + 7)$根
C.$(7n + 5)$根
D.$(7n + 2)$根
D
)小木棒。
A.$(7n + 9)$根
B.$(7n + 7)$根
C.$(7n + 5)$根
D.$(7n + 2)$根
答案:
D
1. 按规律排列的一列数为$0,1,-4,9,-16,25,…$,则第$11$个数是(
A.$-121$
B.$-100$
C.$100$
D.$121$
B
)。A.$-121$
B.$-100$
C.$100$
D.$121$
答案:
B
2. 小明和小亮玩游戏。小明让小亮在心里任想一个数,不说出来,把想好的这个数减去$3$,把所得的差乘以$2$,再减去想好的数的$2$倍。小明准确地说出了小亮算出的结果。这个结果是(
A.$2$
B.$-2$
C.$6$
D.$-6$
D
)。A.$2$
B.$-2$
C.$6$
D.$-6$
答案:
D
3. 观察下列两行数:
$1,5,11,19,29,…$;
$1,3,6,10,15,…$。
取每行的第$7$个数,这两个数的和是(
A.$92$
B.$87$
C.$83$
D.$78$
$1,5,11,19,29,…$;
$1,3,6,10,15,…$。
取每行的第$7$个数,这两个数的和是(
C
)。A.$92$
B.$87$
C.$83$
D.$78$
答案:
C
4. 已知一组数据为$1,\frac{2}{3},\frac{3}{5},\frac{4}{7},…$,则第$n$个数应为(
A.$\frac{n}{n - 2}$
B.$\frac{n}{n + 2}$
C.$\frac{n}{2n - 1}$
D.$\frac{n}{2n + 1}$
C
)。A.$\frac{n}{n - 2}$
B.$\frac{n}{n + 2}$
C.$\frac{n}{2n - 1}$
D.$\frac{n}{2n + 1}$
答案:
C
5. 设一列数中相邻的$3个数依次为m,n,p$,且满足$p = m^{2}-n$。若这列数为$-1,3,-2,a,-7,b,…$,则$b = $
128
。
答案:
128
6. 观察下列等式:
$\frac{1}{1×2}= 1-\frac{1}{2}= \frac{1}{2},$
$\frac{1}{1×2}+\frac{1}{2×3}= 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}= \frac{2}{3},$
$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}= 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}= \frac{3}{4},$
……可知第n个式子的计算结果为
$\frac{1}{1×2}= 1-\frac{1}{2}= \frac{1}{2},$
$\frac{1}{1×2}+\frac{1}{2×3}= 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}= \frac{2}{3},$
$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}= 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}= \frac{3}{4},$
……可知第n个式子的计算结果为
$\frac{n}{n+1}$
(n为正整数,写出最简结果即可)。
答案:
$\frac{n}{n+1}$
7. 小强:“请在心里想好一个数,按照下列步骤进行操作:先把这个数乘$4$,然后加$8$,再乘$5$,再加$7$,最后乘$5$,把最终的结果告诉我,我就知道你心里想的数了。”同学们试了几次,小强都猜对了。你知道这是为什么吗?
答案:
解:设这个数为x,根据题意得5[5(4x+8)+7]=5(20x+40+7)=100x+235,此数减去235后除以100,就可得x的值.
查看更多完整答案,请扫码查看


