第137页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
2. 在长方形ABCD中放入6个长度相同的小长方形,所标尺寸如图所示.设小长方形的宽AE = xcm,依题意可列方程为(

A.6 + 2x = 14 - 3x
B.6 + 2x = x + (14 - 3x)
C.6 + 2x = 14 - x
D.14 - 3x = 6 + 2x
B
).
A.6 + 2x = 14 - 3x
B.6 + 2x = x + (14 - 3x)
C.6 + 2x = 14 - x
D.14 - 3x = 6 + 2x
答案:
B
3. 大家都读过《曹冲称象》的故事吧?按照曹冲的方法,先将象牵到船上,并在船的侧面标记水位,再将象牵出,然后往船上抬入20块等重的条形石,并在船上留3个搬运工,这时水位恰好到达标记位置.如果再抬入1块同样的条形石,船上只留1个搬运工,水位也恰好到达标记的位置.已知每个搬运工体重为90kg,则每块条形石的重量为(
A.120kg
B.140kg
C.160kg
D.180kg
D
).A.120kg
B.140kg
C.160kg
D.180kg
答案:
D
4. 如图,将一段标有0—60的均匀刻度(刻度为整数)的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A,B,C这3段.若这3段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是(
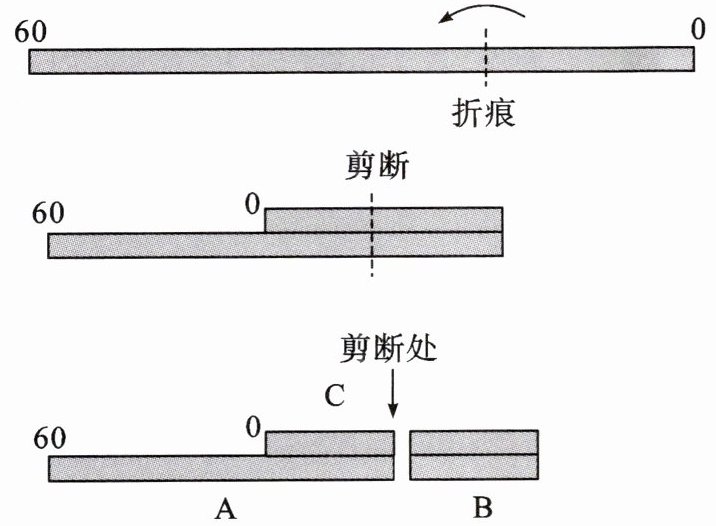
A.20
B.25
C.30
D.35
C
).
A.20
B.25
C.30
D.35
答案:
C
5. 小彬家的墙上钉着一个用彩绳围成的三角形(如图,单位:cm).小彬通过移动钉子,把它变成一个正三角形(如图虚线所示),则正三角形的边长为
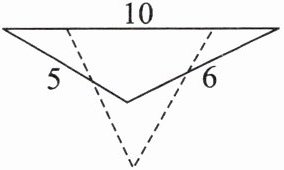
7
cm.
答案:
7
6. 如果一个矩形内部能用一些正方形铺满,这些正方形既不重叠,又无缝隙,就称这个矩形为“优美矩形”.已知如图所示优美矩形ABCD的周长为26,则正方形d的边长为
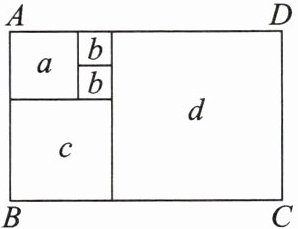
5
.
答案:
5
7. 一个玻璃密封器皿如图①所示,测得它的底面直径为20cm,高为20cm,现内装蓝色溶液若干,如图②放置时,测得液面高10cm;如图③放置时,测得液面高16cm.该玻璃密封器皿的总容量为
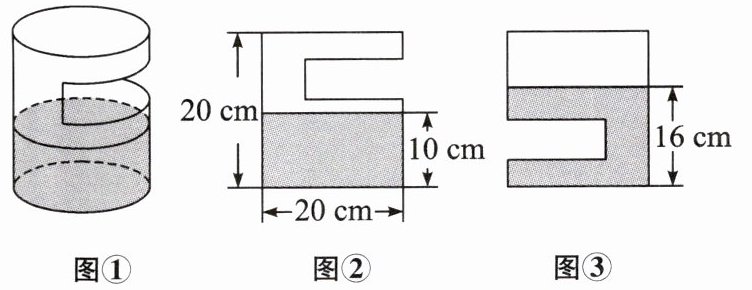
1400π
$cm^3($结果保留π).
答案:
1400π
8. 新年快到了,贫困山区的孩子给资助他们的王老师写了封信,写完后将长方形信纸折叠起来装入信封时发现:若将信纸如图①连续两次对折后,沿着信封口边线装入信封,信封宽绰3.8cm;若将信纸如图②那样3等分折叠后,按同样方法装入信封,信封宽绰1.4cm.试求信纸的长度和信封口的宽度.

9. 底面半径为10cm、高为30cm的圆柱形水桶中装满了水.小明先将桶中的水倒满2个底面半径为3cm、高为5cm的圆柱形杯子,再把剩下的水倒入长、宽、高分别为50cm,20cm,20cm的长方体容器中.长方体容器内水的高度大约是多少厘米?(π取3,容器的厚度不计.)

9. 底面半径为10cm、高为30cm的圆柱形水桶中装满了水.小明先将桶中的水倒满2个底面半径为3cm、高为5cm的圆柱形杯子,再把剩下的水倒入长、宽、高分别为50cm,20cm,20cm的长方体容器中.长方体容器内水的高度大约是多少厘米?(π取3,容器的厚度不计.)
答案:
8.解:设信纸的长度为12x cm,则信封口的宽度为(4x+1.4)cm.根据题意得3x+3.8=4x+1.4,解得x=2.4,
∴12x=28.8,4x+1.4=11(cm).答:信纸的长度为28.8 cm,信封口的宽度为11 cm.9.解:设长方体容器内水的高度大约是x cm,依题意有π×3²×5×2+50×20x=π×10²×30,解得x=8.73.答:长方体容器内水的高度大约是8.73 cm.
∴12x=28.8,4x+1.4=11(cm).答:信纸的长度为28.8 cm,信封口的宽度为11 cm.9.解:设长方体容器内水的高度大约是x cm,依题意有π×3²×5×2+50×20x=π×10²×30,解得x=8.73.答:长方体容器内水的高度大约是8.73 cm.
9. 底面半径为10cm、高为30cm的圆柱形水桶中装满了水.小明先将桶中的水倒满2个底面半径为3cm、高为5cm的圆柱形杯子,再把剩下的水倒入长、宽、高分别为50cm,20cm,20cm的长方体容器中.长方体容器内水的高度大约是多少厘米?(π取3,容器的厚度不计.)
答案:
9.解:设长方体容器内水的高度大约是x cm,依题意有π×3²×5×2+50×20x=π×10²×30,解得x=8.73.答:长方体容器内水的高度大约是8.73 cm.
查看更多完整答案,请扫码查看


