第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
2. 观察算式$(-4)×\dfrac{1}{7}×(-25)×14$,在解题过程中,能使运算变得简便的运算律是(
A.乘法交换律
B.乘法结合律
C.乘法交换律、结合律
D.乘法对加法的分配律
C
).A.乘法交换律
B.乘法结合律
C.乘法交换律、结合律
D.乘法对加法的分配律
答案:
C
3. $\left(-7\dfrac{5}{8}\right)×8$可化为(
A.$-7×\dfrac{5}{8}×8$
B.$-7×8+\dfrac{5}{8}$
C.$-7×8+\dfrac{5}{8}×8$
D.$-7×8-\dfrac{5}{8}×8$
D
).A.$-7×\dfrac{5}{8}×8$
B.$-7×8+\dfrac{5}{8}$
C.$-7×8+\dfrac{5}{8}×8$
D.$-7×8-\dfrac{5}{8}×8$
答案:
D
4. 计算:$(-22)×\dfrac{5}{7}×\left(-\dfrac{3}{11}\right)×(-21)= $
-90
.
答案:
-90
5. 计算:$\dfrac{1}{3}×31-\dfrac{1}{3}×13= \dfrac{1}{3}×$
18
$=6$.
答案:
18
6. 计算下列题.
(1) $\left(-4\dfrac{1}{20}\right)×1.25×(-8)$
(2) $(-10)×(-8.24)×(-0.1)$
(3) $-\dfrac{5}{6}×2.4×\dfrac{3}{5}$
(1) $\left(-4\dfrac{1}{20}\right)×1.25×(-8)$
(2) $(-10)×(-8.24)×(-0.1)$
(3) $-\dfrac{5}{6}×2.4×\dfrac{3}{5}$
答案:
6.解:
(1)原式=$\frac{81}{20}×10=\frac{81}{2}$;
(2)原式=-8.24;
(3)原式=$-\frac{5}{6}×\frac{3}{5}×2.4=-1.2$.
(1)原式=$\frac{81}{20}×10=\frac{81}{2}$;
(2)原式=-8.24;
(3)原式=$-\frac{5}{6}×\frac{3}{5}×2.4=-1.2$.
7. 计算下列题.
(1) $\left(\dfrac{7}{9}-\dfrac{5}{6}+\dfrac{3}{4}-\dfrac{7}{18}\right)×72$
(2) $-\dfrac{3}{4}×\left(8 - 1\dfrac{1}{3}-0.04\right)$
(3) $71\dfrac{15}{16}×(-8)$
(1) $\left(\dfrac{7}{9}-\dfrac{5}{6}+\dfrac{3}{4}-\dfrac{7}{18}\right)×72$
(2) $-\dfrac{3}{4}×\left(8 - 1\dfrac{1}{3}-0.04\right)$
(3) $71\dfrac{15}{16}×(-8)$
答案:
7.解:
(1)原式=$\frac{7}{9}×72-\frac{5}{6}×72+\frac{3}{4}×72-\frac{7}{18}×72=22$;
(2)原式=$-\frac{3}{4}×8+\frac{3}{4}×\frac{4}{3}+\frac{3}{4}×0.04=-4.97$;
(3)原式=$(71+\frac{15}{16})×(-8)=71×(-8)+\frac{15}{16}×(-8)=-568-\frac{15}{2}=-575\frac{1}{2}$.
(1)原式=$\frac{7}{9}×72-\frac{5}{6}×72+\frac{3}{4}×72-\frac{7}{18}×72=22$;
(2)原式=$-\frac{3}{4}×8+\frac{3}{4}×\frac{4}{3}+\frac{3}{4}×0.04=-4.97$;
(3)原式=$(71+\frac{15}{16})×(-8)=71×(-8)+\frac{15}{16}×(-8)=-568-\frac{15}{2}=-575\frac{1}{2}$.
8. 利用运算律有时能进行简便计算.
例 1:$98×12= (100 - 2)×12 = 1200 - 24 = 1176$.
例 2:$-16×233 + 17×233= (-16 + 17)×233 = 233$.
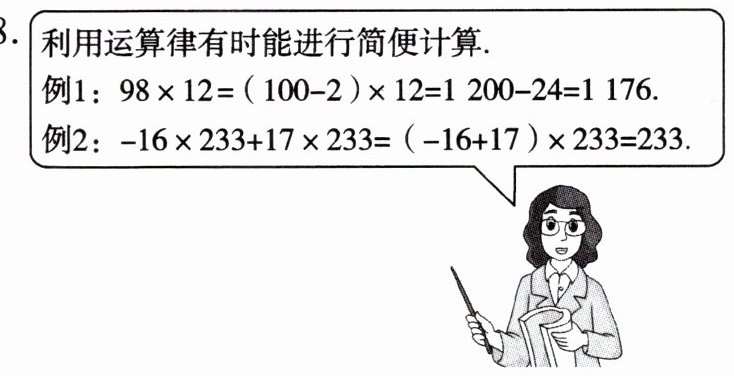
请你参考上面的例题,用运算律简便计算.
(1) $999×(-15)$
(2) $999×118\dfrac{4}{5}+999×\left(-\dfrac{1}{5}\right)-999×18\dfrac{3}{5}$
例 1:$98×12= (100 - 2)×12 = 1200 - 24 = 1176$.
例 2:$-16×233 + 17×233= (-16 + 17)×233 = 233$.

请你参考上面的例题,用运算律简便计算.
(1) $999×(-15)$
(2) $999×118\dfrac{4}{5}+999×\left(-\dfrac{1}{5}\right)-999×18\dfrac{3}{5}$
答案:
8.解:
(1)$999×(-15)=(1000-1)×(-15)=1000×(-15)+15=-15000+15=-14985$;
(2)$999×118\frac{4}{5}+999×(-\frac{1}{5})-999×18\frac{3}{5}=999×(118\frac{4}{5}-\frac{1}{5}-18\frac{3}{5})=999×100=99900$.
(1)$999×(-15)=(1000-1)×(-15)=1000×(-15)+15=-15000+15=-14985$;
(2)$999×118\frac{4}{5}+999×(-\frac{1}{5})-999×18\frac{3}{5}=999×(118\frac{4}{5}-\frac{1}{5}-18\frac{3}{5})=999×100=99900$.
查看更多完整答案,请扫码查看


