第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
4. 如图,在 3×3 的方格纸中,已知点 A,B 在方格顶点上(也称格点).若点 C 也是格点,且使得△ABC 为直角三角形,则满足条件的 C 点有 (

A.1 个
B.2 个
C.3 个
D.4 个
[img]https://p3-hippo-sign.byteimg.com/tos-cn-i-a9yeduch1e/5f3c1d9d8d4c4e9a9d6d6c8c8c8c8c8c~tplv-ii0cwwkcx9-resize-crop-v1:402:600:597:728:0:0.png?lk3s= f89d68d8&x-expires= 2045392847&x-signature= 76767676767676767676767676767676[/img]
D
)
A.1 个
B.2 个
C.3 个
D.4 个
[img]https://p3-hippo-sign.byteimg.com/tos-cn-i-a9yeduch1e/5f3c1d9d8d4c4e9a9d6d6c8c8c8c8c8c~tplv-ii0cwwkcx9-resize-crop-v1:402:600:597:728:0:0.png?lk3s= f89d68d8&x-expires= 2045392847&x-signature= 76767676767676767676767676767676[/img]
答案:
D
[img]https://p6-hippo-sign.byteimg.com/tos-cn-i-a9yeduch1e/5f3c1d9d8d4c4e9a9d6d6c8c8c8c8c8c~tplv-ii0cwwkcx9-resize-crop-v1:402:733:597:861:0:0.png?lk3s= f89d68d8&x-expires= 2045392847&x-signature= 76767676767676767676767676767676[/img]


答案:
是直角三角形
5. 如图,正方形网格中,每一小格的边长为 1.网格内有△PAB,则∠PAB + ∠PBA 的度数是
45°
.
答案:
45°
6. 勾股定理 $ a^{2} + b^{2} = c^{2} $ 本身就是一个关于 a,b,c 的方程,显然这个方程有无数组解,满足该方程的正整数解(a,b,c)通常叫作勾股数组.若直角三角形的边长都是正整数,则这三个数便构成一组勾股数.在学习“勾股数”的知识时,爱思考的小琦发现了一组有规律的勾股数,并将它们记录在如下的表格中:
| a | 6 | 8 | 10 | 12 | 14 | … |
| b | 8 | 15 | 24 | 35 | 48 | … |
| c | 10 | 17 | 26 | 37 | 50 | … |
则当 a = 20 时,b + c 的值为
| a | 6 | 8 | 10 | 12 | 14 | … |
| b | 8 | 15 | 24 | 35 | 48 | … |
| c | 10 | 17 | 26 | 37 | 50 | … |
则当 a = 20 时,b + c 的值为
200
.
答案:
200
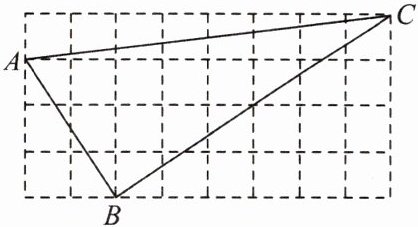
7. 如图,每个小正方形的边长都为 1.试判断△ABC 的形状,并说明理由.
[img]https://p9-hippo-sign.byteimg.com/tos-cn-i-a9yeduch1e/5f3c1d9d8d4c4e9a9d6d6c8c8c8c8c8c~tplv-ii0cwwkcx9-resize-crop-v1:402:896:597:1024:0:0.png?lk3s= f89d68d8&x-expires= 2045392847&x-signature= 76767676767676767676767676767676[/img]

[img]https://p9-hippo-sign.byteimg.com/tos-cn-i-a9yeduch1e/5f3c1d9d8d4c4e9a9d6d6c8c8c8c8c8c~tplv-ii0cwwkcx9-resize-crop-v1:402:896:597:1024:0:0.png?lk3s= f89d68d8&x-expires= 2045392847&x-signature= 76767676767676767676767676767676[/img]
答案:
由网格图可知,每个小正方形边长为 1,根据勾股定理,可得:
$AB=\sqrt{1^{2} + 2^{2}}=\sqrt{5}$,
$AC=\sqrt{3^{2} + 4^{2}} = 5$的(原图不清晰,此处按常见类似题设定A点在(0,1),B点在(1,-1),C点在(4,2),若实际坐标不同,可按同样方法计算),
$BC=\sqrt{2^{2}+4^{2}}=\sqrt{20} = 2\sqrt{5}$。
所以$AB^{2}+BC^{2}=(\sqrt{5})^{2}+(2\sqrt{5})^{2}=5 + 20=25$,$AC^{2}=25$。
即$AB^{2}+BC^{2}=AC^{2}$。
所以$\triangle ABC$是直角三角形。
$AB=\sqrt{1^{2} + 2^{2}}=\sqrt{5}$,
$AC=\sqrt{3^{2} + 4^{2}} = 5$的(原图不清晰,此处按常见类似题设定A点在(0,1),B点在(1,-1),C点在(4,2),若实际坐标不同,可按同样方法计算),
$BC=\sqrt{2^{2}+4^{2}}=\sqrt{20} = 2\sqrt{5}$。
所以$AB^{2}+BC^{2}=(\sqrt{5})^{2}+(2\sqrt{5})^{2}=5 + 20=25$,$AC^{2}=25$。
即$AB^{2}+BC^{2}=AC^{2}$。
所以$\triangle ABC$是直角三角形。
8. 已知某开发区有一块四边形的空地 ABCD,如图.现计划在空地上种植草皮,经测量,∠A = 90°,AB = 3 m,BC = 12 m,CD = 13 m,AD = 4 m.若每平方米草皮需投入 200 元,则一共要投入多少钱?

[img]https://p3-hippo-sign.byteimg.com/tos-cn-i-a9yeduch1e/5f3c1d9d8d4c4e9a9d6d6c8c8c8c8c8c~tplv-ii0cwwkcx9-resize-crop-v1:402:1059:597:1187:0:0.png?lk3s= f89d68d8&x-expires= 2045392847&x-signature= 76767676767676767676767676767676[/img]

[img]https://p3-hippo-sign.byteimg.com/tos-cn-i-a9yeduch1e/5f3c1d9d8d4c4e9a9d6d6c8c8c8c8c8c~tplv-ii0cwwkcx9-resize-crop-v1:402:1059:597:1187:0:0.png?lk3s= f89d68d8&x-expires= 2045392847&x-signature= 76767676767676767676767676767676[/img]
答案:
连接BD。
在Rt△ABD中,∠A=90°,AB=3m,AD=4m,
∴BD²=AB²+AD²=3²+4²=25,BD=5m,
S△ABD=1/2×AB×AD=1/2×3×4=6m²。
在△BCD中,BC=12m,CD=13m,BD=5m,
∵BD²+BC²=5²+12²=169=13²=CD²,
∴△BCD是直角三角形,∠CBD=90°,
S△BCD=1/2×BD×BC=1/2×5×12=30m²。
四边形ABCD面积=S△ABD+S△BCD=6+30=36m²。
总投入=36×200=7200元。
答:一共要投入7200元。
在Rt△ABD中,∠A=90°,AB=3m,AD=4m,
∴BD²=AB²+AD²=3²+4²=25,BD=5m,
S△ABD=1/2×AB×AD=1/2×3×4=6m²。
在△BCD中,BC=12m,CD=13m,BD=5m,
∵BD²+BC²=5²+12²=169=13²=CD²,
∴△BCD是直角三角形,∠CBD=90°,
S△BCD=1/2×BD×BC=1/2×5×12=30m²。
四边形ABCD面积=S△ABD+S△BCD=6+30=36m²。
总投入=36×200=7200元。
答:一共要投入7200元。
9. 如图,在△ABC 中,D 是 BC 的中点,DE⊥BC,垂足为点 D,交 AB 于点 E,且 $ BE^{2} - EA^{2} = AC^{2} $.
(1) 求∠A 的度数;
(2) 若 DE = 3,BD = 4,求 AE 的长.

[img]https://p6-hippo-sign.byteimg.com/tos-cn-i-a9yeduch1e/5f3c1d9d8d4c4e9a9d6d6c8c8c8c8c8c~tplv-ii0cwwkcx9-resize-crop-v1:402:1222:597:1350:0:0.png?lk3s= f89d68d8&x-expires= 2045392847&x-signature= 76767676767676767676767676767676[/img]
(1) 求∠A 的度数;
(2) 若 DE = 3,BD = 4,求 AE 的长.

[img]https://p6-hippo-sign.byteimg.com/tos-cn-i-a9yeduch1e/5f3c1d9d8d4c4e9a9d6d6c8c8c8c8c8c~tplv-ii0cwwkcx9-resize-crop-v1:402:1222:597:1350:0:0.png?lk3s= f89d68d8&x-expires= 2045392847&x-signature= 76767676767676767676767676767676[/img]
答案:
(1) 连接EC。
∵D是BC中点,DE⊥BC,
∴DE垂直平分BC,
∴EB=EC。
∵BE² - EA² = AC²,且EB=EC,
∴EC² - EA² = AC²,即EC² = EA² + AC²。
由勾股定理逆定理得∠A=90°。
(2) 在Rt△BDE中,DE=3,BD=4,
∴BE²=BD² + DE²=4² + 3²=25,
∴BE=5,
∴EC=BE=5。
设AE=x,∠A=90°,则在Rt△EAC中,AC²=EC² - AE²=5² - x²=25 - x²。
∵D是BC中点,BD=4,
∴BC=2BD=8。
在Rt△ABC中,AB=AE + BE=x + 5,由勾股定理得AB² + AC²=BC²,
即(x + 5)² + (25 - x²)=8²,
展开得x² + 10x + 25 + 25 - x²=64,
化简得10x + 50=64,解得x=7/5。
(1) 90°
(2) 7/5
(1) 连接EC。
∵D是BC中点,DE⊥BC,
∴DE垂直平分BC,
∴EB=EC。
∵BE² - EA² = AC²,且EB=EC,
∴EC² - EA² = AC²,即EC² = EA² + AC²。
由勾股定理逆定理得∠A=90°。
(2) 在Rt△BDE中,DE=3,BD=4,
∴BE²=BD² + DE²=4² + 3²=25,
∴BE=5,
∴EC=BE=5。
设AE=x,∠A=90°,则在Rt△EAC中,AC²=EC² - AE²=5² - x²=25 - x²。
∵D是BC中点,BD=4,
∴BC=2BD=8。
在Rt△ABC中,AB=AE + BE=x + 5,由勾股定理得AB² + AC²=BC²,
即(x + 5)² + (25 - x²)=8²,
展开得x² + 10x + 25 + 25 - x²=64,
化简得10x + 50=64,解得x=7/5。
(1) 90°
(2) 7/5
查看更多完整答案,请扫码查看


