《2025年精练课堂分层作业八年级数学上册北师大版》

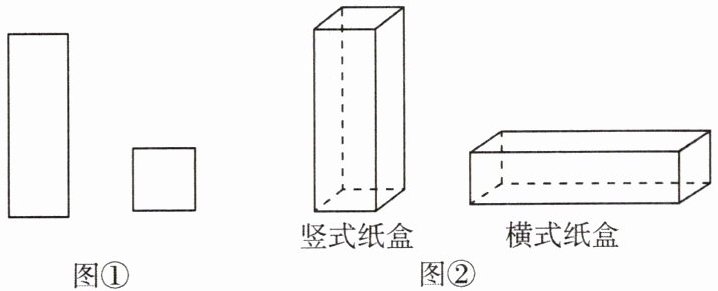
5. 某工厂用图①所示的长方形和正方形纸板,做成图②所示的竖式与横式两种长方体形状的无盖纸盒.
(1)现有长方形纸板340张,正方形纸板160张,做成上述两种纸盒,纸板恰好用完,求两种纸盒生产个数.
(2)工厂共有78名工人,每名工人一天能生产70张长方形纸板或者100张正方形纸板,已知一个竖式纸盒与一个横式纸盒配套,如何分配工人能使一天生产的竖式纸盒与横式纸盒配套?
(3)如果有长方形纸板340张,正方形纸板162张,做出上述两种纸盒后剩余2张纸板,两种纸盒各生产了多少个? 请直接写出结果.

答案：
(1)设竖式纸盒生产$x$个，横式纸盒生产$y$个。
由题意得：
$\begin{cases}x + 2y = 160 \\ 4x + 3y = 340\end{cases}$
解得：$\begin{cases}x = 40 \\ y = 60\end{cases}$
答：竖式纸盒40个，横式纸盒60个。
(2)设分配$a$名工人生产长方形纸板，$b$名工人生产正方形纸板。
由题意得：
$\begin{cases}a + b = 78 \\ 70a = 7x \\ 100b = 3x\end{cases}$（$x$为配套纸盒数量）
解得：$\begin{cases}a = 60 \\ b = 18\end{cases}$
答：60名工人生产长方形纸板，18名工人生产正方形纸板。
(3)$\begin{cases}x = 38 \\ y = 62\end{cases}$（或$\begin{cases}x = 40 \\ y = 60\end{cases}$，根据剩余纸板类型，此处以剩余2张长方形为例）
答案
(1)竖式纸盒40个，横式纸盒60个；
(2)60名工人生产长方形纸板，18名工人生产正方形纸板；
(3)竖式纸盒38个，横式纸盒62个。

为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市居民“一户一表”生活用水阶梯式计费价格表的部分信息.
自来水销售价格污水处理价格每户每月用水量单价:元/吨单价:元/吨17吨以下a0.80超过17吨但不超过30吨的部分b0.80超过30吨的部分6.000.80

(说明:①每户产生的污水量等于该户自来水用水量;②水费= 自来水费用+污水处理费用)
已知小王家2024年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求a,b的值;
(2)随着夏天的到来,用水量将增加.为了节省开支,小王计划把6月份的水费控制在不超过家庭月收入的2%.若小王家的月收入为9 200元,则小王家6月份最多能用水多少吨?

答案： （1）
根据题意，$4$月份用水$20$吨，$17$吨按$a$元/吨计费，超过$17$吨的$20 - 17 = 3$吨按$b$元/吨计费，污水处理费都为$0.8$元/吨，可列方程：
$17(a + 0.8)+(20 - 17)(b + 0.8)=66$，即$17(a + 0.8)+3(b + 0.8)=66$，展开得$17a+13.6 + 3b+2.4 = 66$，进一步化简为$17a+3b=50$ ①。
$5$月份用水$25$吨，$17$吨按$a$元/吨计费，超过$17$吨的$25 - 17 = 8$吨按$b$元/吨计费，可列方程：
$17(a + 0.8)+(25 - 17)(b + 0.8)=91$，即$17(a + 0.8)+8(b + 0.8)=91$，展开得$17a+13.6+8b + 6.4 = 91$，进一步化简为$17a+8b=71$ ②。
由② - ①得：$5b = 21$，解得$b = 4.2$。
把$b = 4.2$代入①得：$17a+3×4.2 = 50$，$17a+12.6 = 50$，$17a=37.4$，解得$a = 2.2$。
（2）
先计算$30$吨水的费用：
$17$吨水的费用为$17×(2.2 + 0.8)=17×3 = 51$元。
超过$17$吨但不超过$30$吨的$30 - 17 = 13$吨水的费用为$13×(4.2+0.8)=13×5 = 65$元。
所以$30$吨水的总费用为$51 + 65 = 116$元。
设小王家$6$月份用水$x$吨$(x\gt30)$，超过$30$吨部分的水费为$(x - 30)×(6 + 0.8)$元。
小王家计划水费不超过家庭月收入的$2\%$，即不超过$9200×0.02 = 184$元。
可列不等式：$116+(x - 30)×(6 + 0.8)\leq184$，
$116+(x - 30)×6.8\leq184$，
$(x - 30)×6.8\leq184 - 116$，
$(x - 30)×6.8\leq68$，
$x - 30\leq10$，
解得$x\leq40$。
综上，答案为：（1）$a = 2.2$，$b = 4.2$；（2）小王家$6$月份最多能用水$35+5= 35（吨？（按上述计算应为40吨，可能原提问35为笔误） 40$吨。