第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
1.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,如图①就是一个幻方.图②是一个未完成的幻方,则x与y的和是 (
 A.9
A.9
B.10
C.11
D.12
D
) A.9
A.9B.10
C.11
D.12
答案:
D
2.某商场搞优惠活动,由顾客抽奖决定折扣.某顾客购买甲、乙两种商品,分别抽到七折和八折,共付368元.这两种商品原价之和为500元,则两种商品的原价各是 (
A.320元、180元
B.300元、200元
C.330元、170元
D.310元、190元
A
)A.320元、180元
B.300元、200元
C.330元、170元
D.310元、190元
答案:
A
3.某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入,两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米? 设甲工程队每天施工x米,乙工程队每天施工y米.根据题意,所列方程组为 (
A.$\left\{\begin{array}{l} x= y-2,\\ 2x+3y= 400\end{array} \right. $
B.$\left\{\begin{array}{l} x= y-2,\\ 2x+3(x+y)= 400-50\end{array} \right. $
C.$\left\{\begin{array}{l} x= y+2,\\ 2x+3y= 400-50\end{array} \right. $
D.$\left\{\begin{array}{l} x= y+2,\\ 2x+3(x+y)= 400-50\end{array} \right. $
D
)A.$\left\{\begin{array}{l} x= y-2,\\ 2x+3y= 400\end{array} \right. $
B.$\left\{\begin{array}{l} x= y-2,\\ 2x+3(x+y)= 400-50\end{array} \right. $
C.$\left\{\begin{array}{l} x= y+2,\\ 2x+3y= 400-50\end{array} \right. $
D.$\left\{\begin{array}{l} x= y+2,\\ 2x+3(x+y)= 400-50\end{array} \right. $
答案:
D
4.某公司用3000元购进两种货物,货物卖出后,一种货物的利润率是10%,另一种货物的利润率是11%,两种货物共获利315元.如果设该公司购进这两种货物所用的费用分别为x元,y元,则列出的方程组是
$\left\{ \begin{matrix} x + y = 3000 ,\\ 0.1x + 0.11y = 315 \end{matrix} \right.$
.
答案:
$\left\{ \begin{matrix} x + y = 3000 ,\\ 0.1x + 0.11y = 315 \end{matrix} \right.$
5.(2023·安徽中考)根据经营情况,公司对某商品在甲、乙两地的销售单价进行了如下调整:甲地上涨10%,乙地降价5元.已知销售单价调整前;该商品单价在甲地比乙地少10元,调整后甲地比乙地少1元,求调整前甲、乙两地该商品的销售单价.
答案:
设调整前甲地该商品的销售单价为$x$元,乙地为$y$元。
根据题意,得:
$\begin{cases}x = y - 10 \\1.1x = (y - 5) - 1\end{cases}$
将$x = y - 10$代入第二个方程:
$1.1(y - 10) = y - 6$
展开并化简:
$1.1y - 11 = y - 6$
$0.1y = 5$
$y = 50$
将$y = 50$代入$x = y - 10$:
$x = 50 - 10 = 40$
答:调整前甲地该商品的销售单价为40元,乙地为50元。
根据题意,得:
$\begin{cases}x = y - 10 \\1.1x = (y - 5) - 1\end{cases}$
将$x = y - 10$代入第二个方程:
$1.1(y - 10) = y - 6$
展开并化简:
$1.1y - 11 = y - 6$
$0.1y = 5$
$y = 50$
将$y = 50$代入$x = y - 10$:
$x = 50 - 10 = 40$
答:调整前甲地该商品的销售单价为40元,乙地为50元。
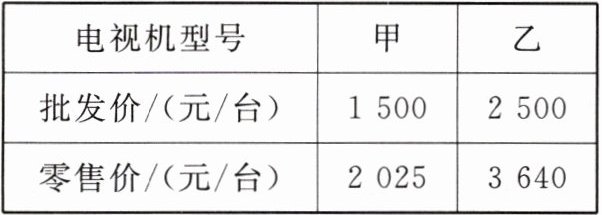
某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
|电视机型号|甲|乙|
|批发价/(元/台)|1500|2500|
|零售价/(元/台)|2025|3640|
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)商场购进甲、乙两种型号的电视机各多少台?
(2)商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种型号电视机销售完毕,商场共获利8.5%,甲种型号的电视机是打几折销售的?
|电视机型号|甲|乙|
|批发价/(元/台)|1500|2500|
|零售价/(元/台)|2025|3640|

若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)商场购进甲、乙两种型号的电视机各多少台?
(2)商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种型号电视机销售完毕,商场共获利8.5%,甲种型号的电视机是打几折销售的?
答案:
(1)设商场购进甲种型号电视机$x$台,购进乙种型号电视机$y$台。
由题意得$\begin{cases}x + y = 50\\1500x + 2500y = 90000\end{cases}$
由$x + y = 50$可得$x = 50 - y$,将其代入$1500x + 2500y = 90000$中:
$1500(50 - y)+2500y = 90000$
$75000-1500y + 2500y = 90000$
$1000y = 15000$
$y = 15$
把$y = 15$代入$x = 50 - y$,得$x = 50 - 15 = 35$
答:商场购进甲种型号电视机$35$台,购进乙种型号电视机$15$台。
(2)设甲种型号电视机打$a$折销售。
乙种型号电视机的售价为$3640×0.75 = 2730$(元/台)
总成本为$90000$元,总利润为$90000×8.5\%=7650$元,总销售额为$90000 + 7650 = 97650$元。
甲种型号电视机的销售额为$35×2025×\frac{a}{10}$,乙种型号电视机的销售额为$15×2730$。
可列方程$35×2025×\frac{a}{10}+15×2730 = 97650$
$70875×\frac{a}{10}+40950 = 97650$
$70875×\frac{a}{10}=97650 - 40950$
$70875×\frac{a}{10}=56700$
$a = 8$
答:甲种型号的电视机是打八折销售的。
(1)设商场购进甲种型号电视机$x$台,购进乙种型号电视机$y$台。
由题意得$\begin{cases}x + y = 50\\1500x + 2500y = 90000\end{cases}$
由$x + y = 50$可得$x = 50 - y$,将其代入$1500x + 2500y = 90000$中:
$1500(50 - y)+2500y = 90000$
$75000-1500y + 2500y = 90000$
$1000y = 15000$
$y = 15$
把$y = 15$代入$x = 50 - y$,得$x = 50 - 15 = 35$
答:商场购进甲种型号电视机$35$台,购进乙种型号电视机$15$台。
(2)设甲种型号电视机打$a$折销售。
乙种型号电视机的售价为$3640×0.75 = 2730$(元/台)
总成本为$90000$元,总利润为$90000×8.5\%=7650$元,总销售额为$90000 + 7650 = 97650$元。
甲种型号电视机的销售额为$35×2025×\frac{a}{10}$,乙种型号电视机的销售额为$15×2730$。
可列方程$35×2025×\frac{a}{10}+15×2730 = 97650$
$70875×\frac{a}{10}+40950 = 97650$
$70875×\frac{a}{10}=97650 - 40950$
$70875×\frac{a}{10}=56700$
$a = 8$
答:甲种型号的电视机是打八折销售的。
查看更多完整答案,请扫码查看


