《2025年精练课堂分层作业八年级数学上册北师大版》

10. 勾股定理神秘而美妙,它的证法多样,各有妙处,其中的“面积法”给了小聪灵感.他惊喜地发现：当两个全等的直角三角形如图①或图②摆放时,都可以用“面积法”来证明.下面是小聪利用图①证明勾股定理的过程：
将两个全等的直角三角形按图①摆放,其中∠DAB = 90°.求证：a^2 + b^2 = c^2.
证明：连接 DB,过点 D 作 BC 边上的高 DF,则 DF = EC = b - a.∵ S_{四边形ADCB} = S_{△ACD} + S_{△ABC} = $\frac{1}{2}$b^2 + $\frac{1}{2}$ab,
又∵ S_{四边形ADCB} = S_{△ADB} + S_{△DCB} = $\frac{1}{2}$c^2 + $\frac{1}{2}$a(b - a),∴ $\frac{1}{2}$b^2 + $\frac{1}{2}$ab = $\frac{1}{2}$c^2 + $\frac{1}{2}$a(b - a).∴ a^2 + b^2 = c^2.
请参照上述证法,利用图②完成下面的证明：
将两个全等的直角三角形按图②摆放,其中∠DAB = 90°.
求证：a^2 + b^2 = c^2.
证明：连接BD，过点 B 作 DE 边上的高 BF，则 BF = b - a.
∵ S_{五边形ACBED} = $S_{△ACB} + S_{△ABE} + S_{△ADE} =\frac{1}{2}ab + \frac{1}{2}b^2 + \frac{1}{2}ab$,
又∵ S_{五边形ACBED} = $S_{△ACB} + S_{△ABD} + S_{△BDE} = \frac{1}{2}ab + \frac{1}{2}c^2 + \frac{1}{2}a(b - a)$,
∴ $\frac{1}{2}ab + \frac{1}{2}b^2 + \frac{1}{2}ab = \frac{1}{2}ab + \frac{1}{2}c^2 + \frac{1}{2}a(b - a)$.
∴ a^2 + b^2 = c^2.

答案： 证明：连接 BD，过点 B 作 DE 边上的高 BF，则 BF = b - a。
∵ $S_{五边形ACBED} = S_{△ACB} + S_{△ABE} + S_{△ADE} $= $\frac{1}{2}ab + \frac{1}{2}b^2 + \frac{1}{2}ab$，
又
∵$ S_{五边形ACBED} = S_{△ACB} + S_{△ABD} + S_{△BDE}$ = $\frac{1}{2}ab + \frac{1}{2}c^2 + \frac{1}{2}a(b - a)$，
∴ $\frac{1}{2}ab + \frac{1}{2}b^2 + \frac{1}{2}ab = \frac{1}{2}ab + \frac{1}{2}c^2 + \frac{1}{2}a(b - a)$。
∴ $a^2 + b^2 = c^2$。

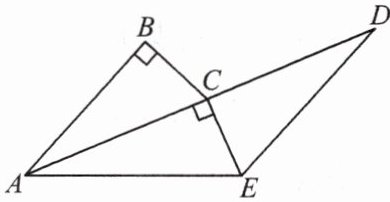
11. 如图,在△ABC 和△DCE 中,AC = DE,∠B = ∠DCE = 90°,点 A,C,D 依次在同一条直线上,且 AB // DE.
(1) 求证：△ABC ≌ △DCE.
(2) 连接 AE,当 BC = 5,AC = 12 时,求 AE 的长.

答案：
(1)见证明过程；
(2)13

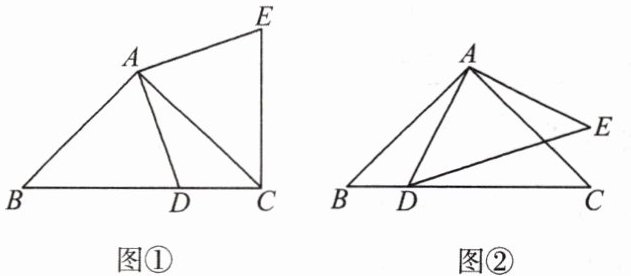
12. 问题：如图①,在 Rt△ABC 中,AB = AC,D 为 BC 边上一点(不与点 B,C 重合),将线段 AD 绕点 A 按逆时针方向旋转 90°得到 AE,连接 EC,则线段 BC,DC,EC 之间满足的等量关系式为BC=DC+EC；
探究：如图②,在 Rt△ABC 与 Rt△ADE 中,AB = AC,AD = AE,将△ADE 绕点 A 旋转,使点 D 落在 BC 边上.探索线段 AD,BD,CD 之间满足的等量关系,并证明你的结论.

答案： 问题：
BC=DC+EC
证明：
∵AB=AC，∠BAC=90°，
∴△ABC为等腰直角三角形。
∵AD绕点A逆时针旋转90°得AE，
∴AD=AE，∠DAE=90°。
∵∠BAC=∠DAE=90°，
∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE。
在△ABD和△ACE中，
$\begin{cases} AB=AC \\ ∠BAD=∠CAE \\ AD=AE \end{cases}$，
∴△ABD≌△ACE（SAS），
∴BD=EC。
∵BC=BD+DC，
∴BC=EC+DC。
探究：
BD²+CD²=2AD²
证明：
连接CE。
∵AB=AC，AD=AE，∠BAC=∠DAE=90°，
∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE。
在△ABD和△ACE中，
$\begin{cases} AB=AC \\ ∠BAD=∠CAE \\ AD=AE \end{cases}$，
∴△ABD≌△ACE（SAS），
∴BD=CE，∠ACE=∠ABD=45°。
∵∠ACB=45°，
∴∠DCE=∠ACB+∠ACE=45°+45°=90°，
∴△DCE为直角三角形，
∴DC²+CE²=DE²。
∵△ADE为等腰直角三角形，
∴DE²=AD²+AE²=2AD²。
∵CE=BD，
∴BD²+CD²=2AD²。
答案
问题：BC=DC+EC；
探究：BD²+CD²=2AD²。