第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
4. 长和宽分别为3和2的长方形,它的对角线长必定是 (
A.整数
B.分数
C.有理数
D.无理数
D
)A.整数
B.分数
C.有理数
D.无理数
答案:
D
5. 下图是棱长为1的正方体,有一只蚂蚁从点$A爬到点C'$去吃糖,则最短路线的长度是 (
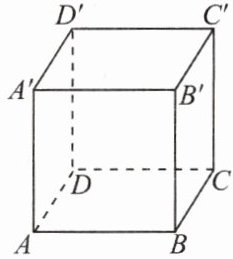
A.无理数
B.分数
C.可能是有理数,也可能是无理数
D.整数
A
)
A.无理数
B.分数
C.可能是有理数,也可能是无理数
D.整数
答案:
A
6. 在$\frac{1}{3},\pi,2.030\ 030\ 003…$(相邻两个3之间0的个数逐次加1),$-1,1.\dot{2}\dot{3},3.214\ 58$中,有理数有
4
个,无理数有2
个.
答案:
4,2
7. 已知正数$m满足m^{2}= 39$,则$m$的整数部分为
6
.
答案:
6
8. (2024 • 滨州中考)写出一个比$\sqrt{3}大且比\sqrt{10}$小的整数:
2(或3)
.
答案:
2(或3)
9. 如图所示,正方形A的面积(阴影部分)是
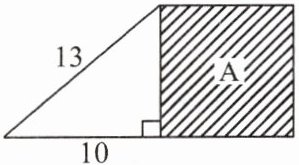
69
,其边长的整数部分是8
,这个正方形的边长是无理数
.(填“有理数”或“无理数”)
答案:
$69$;$8$;无理数
10. 八年级(3)班两名同学在打羽毛球,一不小心球落在离地面约为3m的树上.其中一名同学赶快搬来一架长为4m的梯子,架在树干上.梯子的底端离树干1m远,另一名同学爬上梯子去拿羽毛球.假设这名爬梯子同学的身高与臂长忽略不计,这名同学能拿到球吗?
答案:
设梯子与地面的夹角构成的直角三角形中,梯子为斜边,长度为4m,梯子底端离树干距离为一条直角边,长度为1m。
根据勾股定理,另一条直角边(即梯子能达到的高度)为:
$\sqrt{4^{2} - 1^{2}} = \sqrt{16 - 1} = \sqrt{15} \approx 3.87 \text(m)$
由于3.87m大于3m,
所以,这名同学能拿到球。
根据勾股定理,另一条直角边(即梯子能达到的高度)为:
$\sqrt{4^{2} - 1^{2}} = \sqrt{16 - 1} = \sqrt{15} \approx 3.87 \text(m)$
由于3.87m大于3m,
所以,这名同学能拿到球。
图①是第七届国际数学教育大会(简称ICME - 7)的会徽,会徽的主体图案是由图②所示的一连串直角三角形演化而成的,其中$OA_{1}= A_{1}A_{2}= A_{2}A_{3}=… =A_{7}A_{8}= 1$.如果把图②中的直角三角形继续作下去,那么$OA_{1},OA_{2},OA_{3},…,OA_{25}$这些线段中,有多少条线段的长度为无理数?
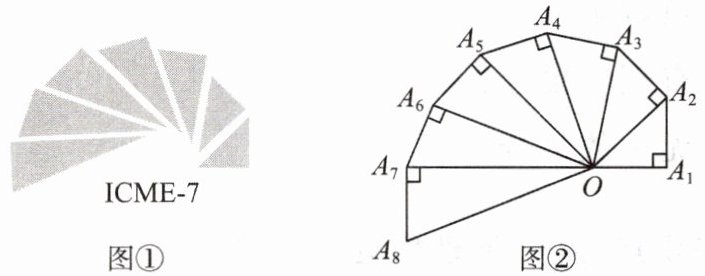

答案:
20
查看更多完整答案,请扫码查看


