《2025年自主学习指导课程与测试七年级数学上册人教版》

8. 做游戏，学数学。
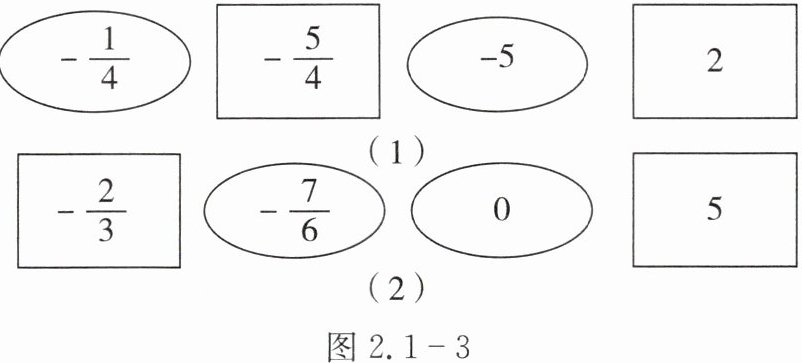
游戏规则：每人每次抽取 $4$ 张卡片，如果抽到椭圆卡片，那么减去卡片上的数；如果抽到长方形卡片，那么加上卡片上的数；最后结果大的为胜者。
小彬依次抽到了如图 $2.1 - 3(1)$ 所示的 $4$ 张卡片，小丽依次抽取到了如图 $2.1 - 3(2)$ 所示的 $4$ 张卡片。问获胜的是谁？请说明理由。

答案： 8.解:小彬获胜,理由如下$:-(-\frac{1}{4})-\frac{5}{4}-(-5)+2=\frac{1}{4}-\frac{5}{4}+5+2=-1+5+2=4+2=6,-\frac{2}{3}-(-\frac{7}{6})-0+5=-\frac{4}{6}+\frac{7}{6}+5=\frac{1}{2}+5=5\frac{1}{2},$因为$6＞5\frac{1}{2},$所以小彬获胜.

9. 如图 $2.1 - 4$，点 $A$，$B$ 在数轴上分别表示有理数 $a$，$b$，$A$，$B$ 两点之间的距离表示为 $AB$，在数轴上 $A$，$B$ 两点之间的距离 $AB = |a - b|$。例如：数轴上表示 $-1$ 与 $-2$ 的两点间的距离 $=| - 1-( - 2)| = - 1 + 2 = 1$；而 $|x + 2| = |x-( - 2)|$，所以 $|x + 2|$ 表示 $x$ 与 $-2$ 两点间的距离。利用数形结合思想回答下列问题。
(1) 数轴上表示 $-2$ 和 $-5$ 两点之间的距离为3。
(2) 若数轴上表示点 $x$ 的数满足 $|x - 3| = 2$，那么 $x=$1或5。
(3) 若数轴上表示点 $x$ 的数满足 $-4\lt x\lt4$，求 $|x - 4|+|x + 4|$ 的值。

答案： 9.解:
(1)3;
(2)1或5;
(3)因为$\vert x-4\vert+\vert x+4\vert$表示在数轴上表示x的点到-4和4的点的距离之和,且x位于-4到4之间,所以x-4＜0,x+4＞0,所以$\vert x-4\vert+\vert x+4\vert=4-x+x+4=8.$