《2025年全效核心素养测评高中数学必修第一册人教版》

8. (多选)下面列出的几种不等关系中，正确的有 (BCD)

A.x与2的和是非负数，该语句可表示为 “$ x + 2 ＞ 0 $”
B.$ \triangle ABC $的两边之和大于第三边，记三边分别为a，b，c，则上述不等关系可表示为 “$ a + b ＞ c $，$ b + c ＞ a $，且 $ a + c ＞ b $”
C.若某天的气温为t，最低气温为7℃，最高气温为13℃，则这天的气温范围可表示为 “7℃ $ \leq t \leq 13 $℃”
D.完成一项装修工程，请木工需支付工资每人400元，请瓦工需支付工资每人500元，要求工人的工资预算不超过20 000元. 设木工x人，瓦工y人，则上述问题用不等关系可表示为 “$ 400x + 500y \leq 20000 $”

答案： 8.BCD

9. (多选)下列不等式中，恒成立的有 (ACD)

A.$ a^{2} + 3 ＞ 2a $
B.$ x^{2} + y^{2} ＞ xy $
C.$ a^{2} + b^{2} \geq 2(a - b - 1) $
D.$ a^{2} + b^{2} \geq 2ab $

答案： 9.ACD

10. 一辆汽车原来每天行驶x km，如果该辆汽车每天行驶的路程比原来多19 km，那么8天内它的行程就超过2 200 km，用不等式表示为8(x + 19) ＞ 2200；如果它每天行驶的路程比原来少12 km，那么它原来行驶8天的路程就得花9天多的时间，用不等式表示为$\frac{8x}{x - 12} ＞ 9$.

答案： $10.8(x + 19) ＞ 2200 \frac{8x}{x - 12} ＞ 9$

11. 将一根长5 m的绳子截成两段，已知其中一段的长度为x m，若两段绳子长度之差不小于1 m，则x所满足的不等关系为.

答案： $11.\begin{cases}\vert 2x - 5\vert \geq 1 \\0 ＜ x ＜ 5\end{cases}$

12. 若 $ a ＜ 0 $，$ -1 ＜ b ＜ 0 $，则将 $ ab $，$ ab^{2} $，a按大小顺序排列为ab ＞ ab^{2} ＞ a(用“＞”连接).

答案： $12.ab ＞ ab^{2} ＞ a$

13. 已知 $ a ＞ 0 $，$ b ＞ 0 $，求证：$ (a^{2} + b^{2})^{2} \geq 4a^{2}b^{2} $，当且仅当 $ a = b $时，等号成立.

答案： 13.证明：$(a^{2} + b^{2})^{2} - 4a^{2}b^{2} = a^{4} + b^{4} + 2a^{2}b^{2} - 4a^{2}b^{2} = a^{4} + b^{4} - 2a^{2}b^{2} = (a^{2} - b^{2})^{2} \geq 0，$当且仅当$a^{2} = b^{2}$时取等号.又a ＞ 0，b ＞ 0，$\therefore (a^{2} + b^{2})^{2} \geq 4a^{2}b^{2}，$当且仅当a = b时，等号成立.

14. 有学生若干个，住若干间宿舍，如果每间住4人，那么还余19人，如果每间住6人，那么只有一间住不满但不空，求宿舍间数和学生人数.

答案： 14.解：设宿舍有x间，则学生有(4x + 19)人，依题意，得
$\begin{cases}4x + 19 ＜ 6x \\4x + 19 ＞ 6(x - 1)\end{cases}$
解得$\frac{19}{2} ＜ x ＜ \frac{25}{2}。$$\because x \in N^{*}，$$\therefore x = 10,11$或12，学生人数分别为59,63,67，故宿舍间数和学生人数分别为10间59人，11间63人或12间67人.

15. 手机的屏幕的面积与整机面积的比值叫做手机的“屏占比”，它是手机外观设计中的一个重要参数，其值通常在0～1之间. 设计师将某手机的屏幕面积和整机面积同时增加相同的数量，升级为一款新的手机外观，则该手机的“屏占比”和升级前比 (C)

A.不变
B.变小
C.变大
D.变化不确定

答案： 15.C

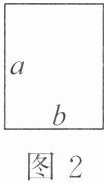
16. 如图所示的两种广告牌，其中图1是由两个等腰直角三角形构成的，图2是一个矩形，从图形上确定这两个广告牌面积的大小关系，并将这种关系用含字母a，b的不等式表示出来为$\frac{1}{2}(a^{2} + b^{2}) ＞ ab$.

答案： $16.\frac{1}{2}(a^{2} + b^{2}) ＞ ab$