《2025年配套综合练习甘肃八年级数学上册人教版》

9. 计算：(1)$\left(\frac{b}{5}\right)^{2}=$$\frac{b^{2}}{25}$；(2)$(4x)^{2}\cdot xy^{2}÷ 2xy=$$8x^{2}y$.

答案：
(1)$\frac{b^{2}}{25}$
(2)$8x^{2}y$

10. 若$(x + 3)(x^{2}-ax + 7)$的乘积中不含$x$的一次项,则$a = $$\frac{7}{3}$.

答案： $\frac{7}{3}$

11. 已知$(x - 1)(x + 2)= ax^{2}+bx + c$,则代数式$4a - 2b + c$的值为0.

答案： 0

12. 若$x^{2}-8x + b可以转化为(x - a)^{2}-2$,则$a + b$的值是18.

答案： 18

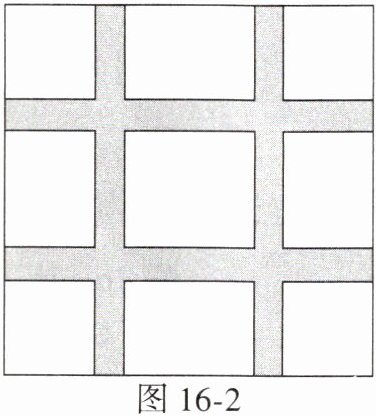
13. 如图 16 - 2,在一块边长为$a$的正方形花圃中,两纵两横的 4 条宽度为$b$的人行道把花圃分成 9 块.由此可以得到的关于$a$,$b$的恒等式是$(a-2b)^{2}=a^{2}-4ab+4b^{2}$.

答案： $(a-2b)^{2}=a^{2}-4ab+4b^{2}$

14. 有甲、乙、丙三种纸片若干张(数据如图 16 - 3,$a\gt b$).
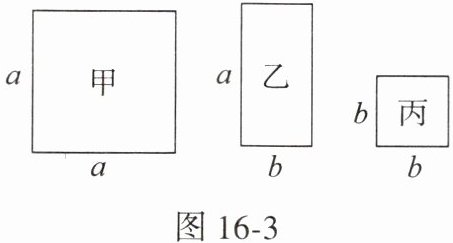
(1)若用这三种纸片紧密拼接成一个边长为$2a + b$的大正方形,则需要取乙纸片4张,丙纸片1张；
(2)若取甲纸片 1 张、乙纸片 3 张、丙纸片 2 张紧密拼成一个长方形,则这个长方形的长为$a+2b$,宽为$a+b$.

答案：
(1)4 1
(2)$a+2b$ $a+b$

15. (6 分)计算：
(1)$2a^{2}b\cdot 5ab^{2}-3ab\cdot (ab)^{2}$；(2)$a^{4}+(-2a^{2})^{3}-a^{8}÷ a^{4}$.

答案： $(1)$计算$2a^{2}b\cdot 5ab^{2}-3ab\cdot (ab)^{2}$
解：
根据单项式乘法法则：单项式与单项式相乘，把它们的系数、同底数幂分别相乘。
计算$2a^{2}b\cdot 5ab^{2}$：
系数相乘$2×5 = 10$，同底数幂相乘$a^{2}\cdot a=a^{2 + 1}=a^{3}$，$b\cdot b^{2}=b^{1 + 2}=b^{3}$，所以$2a^{2}b\cdot 5ab^{2}=10a^{3}b^{3}$。
计算$3ab\cdot (ab)^{2}$：
先算幂的乘方$(ab)^{2}=a^{2}b^{2}$，再算单项式乘法，系数$3×1 = 3$，同底数幂相乘$a\cdot a^{2}=a^{1+2}=a^{3}$，$b\cdot b^{2}=b^{1 + 2}=b^{3}$，所以$3ab\cdot (ab)^{2}=3a^{3}b^{3}$。
则$2a^{2}b\cdot 5ab^{2}-3ab\cdot (ab)^{2}=10a^{3}b^{3}-3a^{3}b^{3}=(10 - 3)a^{3}b^{3}=7a^{3}b^{3}$。
$(2)$计算$a^{4}+(-2a^{2})^{3}-a^{8}÷ a^{4}$
解：
计算$(-2a^{2})^{3}$：
根据积的乘方法则$(ab)^n=a^nb^n$，可得$(-2a^{2})^{3}=(-2)^{3}\cdot(a^{2})^{3}=-8a^{6}$。
计算$a^{8}÷ a^{4}$：
根据同底数幂的除法法则$a^m÷ a^n=a^{m - n}$（$m\gt n$，$a\neq0$），可得$a^{8}÷ a^{4}=a^{8 - 4}=a^{4}$。
则$a^{4}+(-2a^{2})^{3}-a^{8}÷ a^{4}=a^{4}-8a^{6}-a^{4}=(a^{4}-a^{4})-8a^{6}=-8a^{6}$。
综上，答案依次为$(1)\boldsymbol{7a^{3}b^{3}}$；$(2)\boldsymbol{-8a^{6}}$。