《2025年配套综合练习甘肃八年级数学上册人教版》

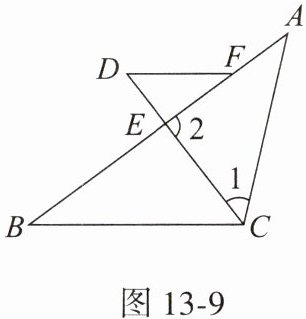
20. (7 分)如图 13 - 9,在 $ \triangle ABC $ 中,$ CD $ 平分 $ \angle ACB $,$ CD $ 交边 $ AB $ 于点 $ E $,在边 $ AE $ 上取点 $ F $,连接 $ DF $,使 $ \angle 1 = \angle D $。
(1)求证：$ DF// BC $；
(2)当 $ \angle A = 40^{\circ} $,$ \angle DFE = 36^{\circ} $ 时,求 $ \angle 2 $ 的度数。

答案：

(1)【证明】

∵ $CD$ 平分 $\angle ACB$，

∴ $\angle DCB = \angle 1$。

又
∵ $\angle 1 = \angle D$，

∴ $\angle DCB = \angle D$，

∴ $DF // BC$。

(2)【解】

∵ $DF // BC$，$\angle DFE = 36^{\circ}$，

∴ $\angle B = \angle DFE = 36^{\circ}$。

在 $\triangle ABC$ 中，$\angle A = 40^{\circ}$，$\angle B = 36^{\circ}$，

∴ $\angle ACB = 180^{\circ} - 40^{\circ} - 36^{\circ} = 104^{\circ}$。

又
∵ $CD$ 平分 $\angle ACB$，

∴ $\angle 1 = \frac{1}{2}\angle ACB = 52^{\circ}$，

∴ $\angle 2 = 180^{\circ} - 40^{\circ} - 52^{\circ} = 88^{\circ}$。

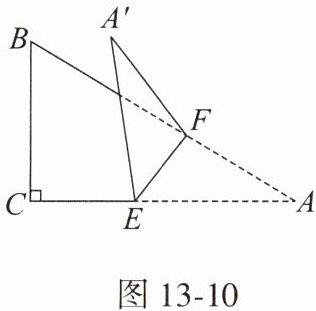
21. (8 分)如图 13 - 10,在 $ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ \angle A = 30^{\circ} $,$ E,F $ 分别是边 $ AC,AB $ 上的点,连接 $ EF $,将 $ \triangle AEF $ 沿 $ EF $ 折叠,得到 $ \triangle A'EF $,当 $ \triangle A'EF $ 的边 $ A'F $ 与 $ \triangle ABC $ 的一边平行时,求 $ \angle AEF $ 的度数。

答案： 情况1：$A'F // AB$
$\because A'F // AB$，$EF$为截线，$\therefore \angle A'FE = \angle BFE$（内错角相等）。
设$\angle AEF = x$，在$\triangle AEF$中，$\angle AFE = 180° - \angle A - \angle AEF = 150° - x$。
由折叠性质，$\angle A'FE = \angle AFE = 150° - x$。
$\because \angle BFE = 180° - \angle AFE = 180° - (150° - x) = 30° + x$，
$\therefore 150° - x = 30° + x$，解得$x = 60°$。
情况2：$A'F // BC$
$\because \angle C = 90°$，$\therefore BC \perp AC$，又$A'F // BC$，$\therefore A'F \perp AC$，即$\angle A'FD = 90°$（$D$为$A'F$与$AC$交点）。
设$\angle AEF = x$，则$\angle AFE = 150° - x$，折叠后$\angle A'FE = 150° - x$。
$\because \angle DFE = \angle A'FD - \angle A'FE = 90° - (150° - x) = x - 60°$，
在$\triangle DEF$中，$\angle DFE = 180° - \angle AEF - 90° = 90° - x$，
$\therefore x - 60° = 90° - x$，解得$x = 75°$。
结论：$\angle AEF$的度数为$60°$或$75°$。
$\boxed{60°}$或$\boxed{75°}$

22. (8 分)阅读下面的材料：
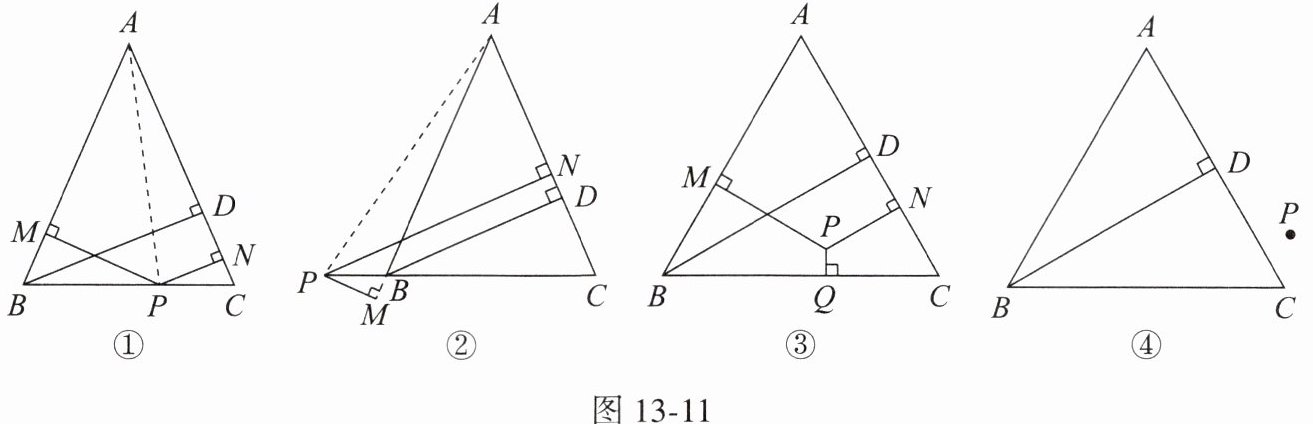
阳阳同学遇到这样一个问题：如图 13 - 11①,在 $ \triangle ABC $ 中,$ AB = AC $,$ BD $ 是 $ \triangle ABC $ 的高,$ P $ 是 $ BC $ 边上一点,$ PM,PN $ 分别与直线 $ AB,AC $ 垂直,垂足分别为点 $ M,N $。求证：$ BD = PM + PN $。
阳阳同学发现,连接 $ AP $,有 $ S_{\triangle ABC} = S_{\triangle ABP}+S_{\triangle ACP} $,即 $ \frac{1}{2}AC\cdot BD = \frac{1}{2}AB\cdot PM+\frac{1}{2}AC\cdot PN $。由 $ AB = AC $,可得 $ BD = PM + PN $。
他又画出了当点 $ P $ 在 $ CB $ 的延长线上,且上面问题中其他条件不变时的图形,如图 13 - 11②所示,他猜想此时 $ BD,PM,PN $ 之间的数量关系是 $ BD = PN - PM $。

(1)请补全阳阳同学证明猜想的过程。
证明：连接 $ AP $,$ \because S_{\triangle ABC} = S_{\triangle APC}- $$ S_{\triangle APB} $,
$ \therefore \frac{1}{2}AC\cdot BD = \frac{1}{2}AC\cdot $$ PN $$ -\frac{1}{2}AB\cdot $$ PM $。
$ \because AB = AC $,$ \therefore BD = PN - PM $。
(2)参考阳阳同学思考问题的方法,解决下列问题：
在 $ \triangle ABC $ 中,$ AB = AC = BC $,$ BD $ 是 $ \triangle ABC $ 的高。$ P $ 是 $ \triangle ABC $ 所在平面上一点,$ PM,PN,PQ $ 分别与直线 $ AB,AC,BC $ 垂直,垂足分别为点 $ M,N,Q $。
①如图 13 - 11③,若点 $ P $ 在 $ \triangle ABC $ 的内部,猜想 $ BD,PM,PN,PQ $ 之间的数量关系并写出推理过程。
②若点 $ P $ 在如图 13 - 11④所示的位置,利用图 13 - 11④探究得此时 $ BD,PM,PN,PQ $ 之间的数量关系：$ BD=PM+PQ-PN $。(直接写出结论即可)
(2)①$ BD=PM+PN+PQ $,推理过程：连接$AP$、$BP$、$CP$，因为$S_{\triangle ABC}=S_{\triangle APB}+S_{\triangle APC}+S_{\triangle BPC}$，所以$\frac{1}{2}AB\cdot BD=\frac{1}{2}AB\cdot PM+\frac{1}{2}AC\cdot PN+\frac{1}{2}BC\cdot PQ$，又因为$AB=AC=BC$，所以$BD=PM+PN+PQ$。

答案： $(1)S_{△APB} PN PM (2)①BD=PM+PN+PQ,$推理过程略. ②BD=PM+PQ-PN