《2025年配套综合练习甘肃八年级数学上册人教版》

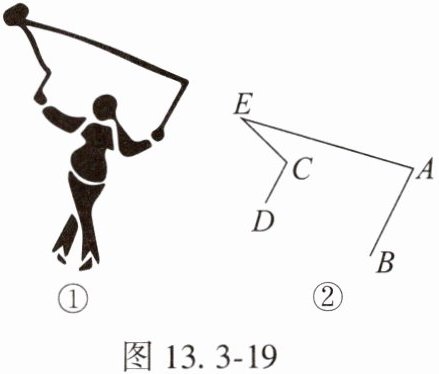
5. 为增强学生体质,感受中国的传统文化,学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间。图 13.3 - 19①是某同学“抖空竹”时的一个瞬间,王聪把它抽象成一个数学问题：如图 13.3 - 19②,已知$AB//CD$,$\angle EAB = 80^{\circ}$,$\angle ECD = 110^{\circ}$,则$\angle E$的度数为30$^{\circ}$。

答案： 30

6. 如图 13.3 - 20,在$\triangle ABC$中,$AD$是角平分线,$\angle B = 50^{\circ}$,$\angle C = 70^{\circ}$。
(1)求$\angle ADB$的度数；

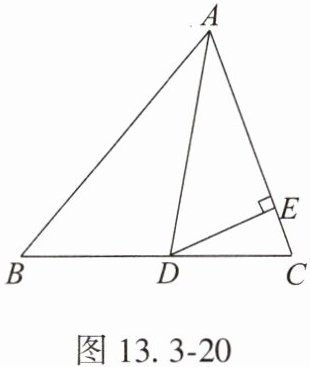
(2)若$DE\perp AC$,求$\angle EDC$的度数。

答案：
(1)∠ADB=100°
(2)∠EDC=20°

7. 综合与探究：在$\triangle ABC$中,$\angle ABC与\angle ACB的平分线相交于点P$。

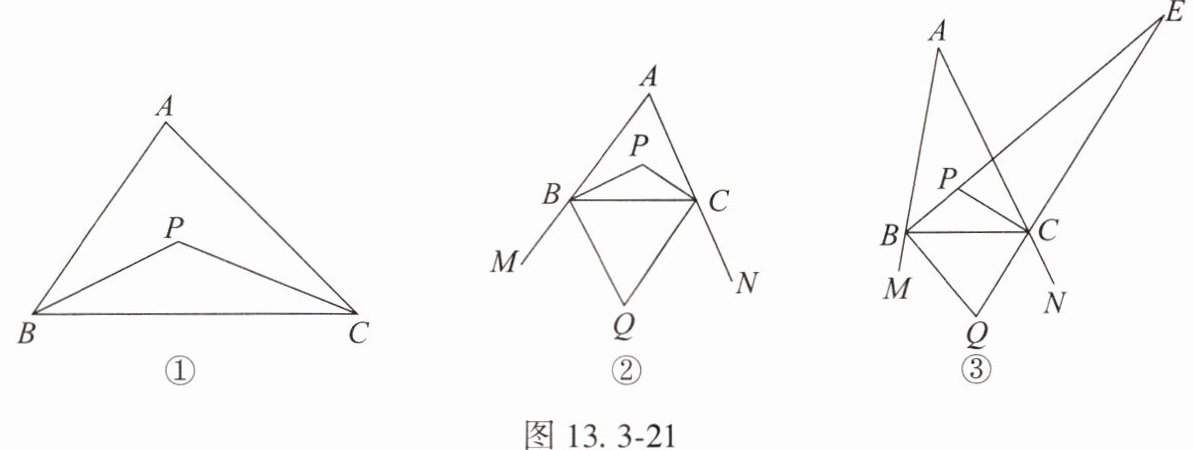
(1)如图 13.3 - 21①,如果$\angle A = 80^{\circ}$,那么$\angle BPC= $130°。
(2)如图 13.3 - 21②,作$\triangle ABC的外角\angle MBC$,$\angle NCB的平分线交于点Q$,试探究$\angle Q与\angle P$的数量关系。
∠Q+∠P=180°
(3)如图 13.3 - 21③,在(2)的条件下,延长线段$BP$,$QC交于点E$,在$\triangle BQE$中,若$\angle Q = 4\angle E$,求$\angle A$的度数。
∠A=36°

答案：
(1)130°
(2)∠Q+∠P=180°
(3)∠A=36°