《2025年作业本江西教育出版社八年级数学上册人教版》

1. 将多项式$a^2x + axy - a^2xy$进行因式分解时,应提取的公因式是(A)
A.$a$
B.$a^2$
C.$ay$
D.$ax$

答案： 【解析】：
本题主要考察多项式的因式分解，特别是提取公因式的方法。
首先，观察多项式 $a^2x + axy - a^2xy$ 的各项，寻找它们的公因式。
公因式是指多项式中各项都含有的因子。
在这个多项式中，可以看到每一项都含有 $a$，但并非每一项都含有 $x$ 或 $y$。
然而，如果考虑 $a$ 的更高次幂，可以发现 $a^2$ 是前两项 $a^2x$ 和 $-a^2xy$ 的公因子，但第三项 $axy$ 只含有一个 $a$。
因此，最大的公因式是 $a$，而不是 $a^2$，$ax$ 或 $ay$。
接下来，可以将这个公因式从多项式中提取出来：
$a^2x + axy - a^2xy = a × ax + a × xy - a × axy = a(ax + xy - axy)$。
但这一步是为了验证公因式的正确性，题目只要求找出公因式，所以答案是 $a$。
【答案】：
A

2. 对于①$x - 3xy = x(1 - 3y)$,②$(x + 3) \cdot (x - 1) = x^2 + 2x - 3$从左到右的变形,表述正确的是(C)
A.都是因式分解
B.都是乘法运算
C.①是分解因式,②是乘法运算
D.①是乘法运算,②是分解因式

答案： 【解析】：
首先，我们需要明确两个概念：因式分解和乘法运算。
因式分解是把一个多项式化为几个整式的积的形式，而乘法运算则是将几个整式相乘得到一个新的多项式。
对于①$x - 3xy = x(1 - 3y)$，我们可以看到左边是一个多项式，右边是将其化为两个整式$x$和$1-3y$的乘积形式，因此①是因式分解。
对于②$(x + 3) \cdot (x - 1) = x^2 + 2x - 3$，左边是两个整式的乘积，右边是它们相乘得到的多项式，因此②是乘法运算。
综上所述，①是分解因式，②是乘法运算。
【答案】：C

3. 下列分解因式中,正确的有(C)
①$x^3 + 2xy + x = x(x^2 + 2y)$；
②$x^2 + 4x + 4 = (x + 2)^2$；
③$-x^2 + y^2 = (x + y)(x - y)$.
A.3个
B.2个
C.1个
D.0个

答案： 【解析】：
本题主要考察因式分解的正确性。
对于①：$x^3 + 2xy + x$，
提取公因式$x$后，得到$x(x^2 + 2y + 1)$，
与给定的$x(x^2 + 2y)$不同，故①错误。
对于②：$x^2 + 4x + 4$，
利用完全平方公式，可以得到$(x + 2)^2$，
与给定的$(x + 2)^2$相同，故②正确。
对于③：$-x^2 + y^2$，
利用平方差公式，应该得到$(y + x)(y - x)$，
与给定的$(x + y)(x - y)$不同，故③错误。
综上，只有②是正确的，所以正确的有1个。
【答案】：C.1个。

4. 若$a$,$b$,$c$是一个三角形的三边长,则$a^2 - b^2 - c^2 - 2bc$＜0.(填“＞”“＜”或“=”)

答案： 解：$a^2 - b^2 - c^2 - 2bc$
$=a^2 - (b^2 + 2bc + c^2)$
$=a^2 - (b + c)^2$
$=(a + b + c)(a - b - c)$
因为$a$，$b$，$c$是三角形的三边长，所以$a + b + c ＞ 0$，且根据三角形三边关系，$a ＜ b + c$，即$a - b - c ＜ 0$。
则$(a + b + c)(a - b - c) ＜ 0$，所以$a^2 - b^2 - c^2 - 2bc ＜ 0$。
＜

5. 新定义：对于任意实数$x$,都有$f(x) = ax^2 + bx$.若$f(1) = 5$,$f(2) = 12$,则将$f(x^2 - 4x)$分解因式的结果为______$x(x - 4)(x - 2)^2$.

答案： 解：由题意得，$f(1)=a×1^2 + b×1 = a + b = 5$，$f(2)=a×2^2 + b×2 = 4a + 2b = 12$。
联立方程组$\begin{cases}a + b = 5 \\ 4a + 2b = 12\end{cases}$，
由第一个方程得$b = 5 - a$，代入第二个方程：
$4a + 2(5 - a) = 12$，
$4a + 10 - 2a = 12$，
$2a = 2$，
$a = 1$，则$b = 5 - 1 = 4$，
所以$f(x) = x^2 + 4x$，
$f(x^2 - 4x) = (x^2 - 4x)^2 + 4(x^2 - 4x)$
$= (x^2 - 4x)(x^2 - 4x + 4)$
$= x(x - 4)(x - 2)^2$
答案：$x(x - 4)(x - 2)^2$

6. 分解因式：
(1)$2x^3 - 8x$；
(2)$(x + y)^2 - 14(x + y) + 49$；
(3)$m(a - 3) + 2(3 - a)$.

答案： 【解析】：
本题主要考察因式分解，包括提取公因式，平方差公式以及完全平方公式的运用。
(1) 对于 $2x^3 - 8x$，首先提取公因式 $2x$，然后对剩余的多项式进行因式分解。
(2) 对于 $(x + y)^2 - 14(x + y) + 49$，观察其形式，可以发现它具有完全平方公式的特点。
(3) 对于 $m(a - 3) + 2(3 - a)$，首先进行变形，然后提取公因式。
【答案】：
(1)解：
原式$= 2x(x^2 - 4)$
$= 2x(x^2 - 2^2)$
$= 2x(x + 2)(x - 2)$
(2)解：
原式$= (x + y)^2 - 2 × 7(x + y) + 7^2$
$= (x + y - 7)^2$
(3)解：
原式$= m(a - 3) - 2(a - 3)$
$= (a - 3)(m - 2)$

7. 如图所示,在一块边长为$a$的正方形木板上,锯掉边长为$b$的4个小正方形.当$a = 18\ dm$,$b = 6\ dm$时,求剩余部分的面积.

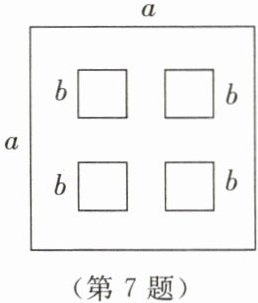
答案： 解：剩余部分的面积 = 大正方形面积 - 4个小正方形面积
大正方形面积为 $a^2$，1个小正方形面积为 $b^2$，则剩余部分面积为 $a^2 - 4b^2$。
当 $a = 18\ dm$，$b = 6\ dm$ 时，
$a^2 - 4b^2 = 18^2 - 4 × 6^2 = 324 - 4 × 36 = 324 - 144 = 180\ dm^2$。
答：剩余部分的面积为 $180\ dm^2$。

8. 某数学活动小组对多项式的乘法计算进行了如下探究：
①$(x + 2)(x + 3) = x^2 + 5x + 6$；
②$(x - 4)(x + 1) = x^2 - 3x - 4$；
③$(y - 5)(y - 3) = y^2 - 8y + 15$.
通过以上计算发现,形如$(x + p)(x + q)$的两个多项式相乘,其结果一定为$x^2 + (p + q)x + pq$($p$,$q$为整数).因为分解因式与整式乘法是方向相反的变形,所以一定有$x^2 + (p + q)x + pq = (x + p)(x + q)$,即可将形如$x^2 + (p + q)x + pq的多项式分解因式成(x + p) \cdot (x + q)$($p$,$q$为整数).
例如：$x^2 + 3x + 2 = x^2 + (1 + 2)x + 1 × 2 = (x + 1)(x + 2)$.
(1)【初步应用】用上面的方法分解因式：$x^2 + 6x + 8 = $______；
(2)【类比应用】若$x^2 + mx + 8$可用以上方法分解因式,则整数$m$的所有可能值是______；
(3)【拓展应用】分解因式：$(x^2 - 4x)^2 - 2(x^2 - 4x) - 15$.

答案： 【解析】：
(1)【初步应用】
考虑$x^2 + 6x + 8$，其中$p + q = 6$，$pq = 8$。
解这个方程组，我们得到$p = 2$，$q = 4$或$p = 4$，$q = 2$。
所以，$x^2 + 6x + 8 = (x + 2)(x + 4)$。
(2)【类比应用】
考虑$x^2 + mx + 8$，其中$pq = 8$。
8的因数对有$(1, 8)$，$(8, 1)$，$(-1, -8)$，$(-8, -1)$，$(2, 4)$，$(4, 2)$，$(-2, -4)$，$(-4, -2)$。
对应的$p + q$的值分别为$9$，$-9$，$6$，$-6$。
所以，整数$m$的所有可能值为$\pm 6$，$\pm 9$。
(3)【拓展应用】
考虑$(x^2 - 4x)^2 - 2(x^2 - 4x) - 15$，令$y = x^2 - 4x$，则原式变为$y^2 - 2y - 15$。
因式分解得$(y - 5)(y + 3)$。
将$y$替换回$x^2 - 4x$，得到$(x^2 - 4x - 5)(x^2 - 4x + 3)$。
进一步分解得$(x - 5)(x + 1)(x - 1)(x - 3)$。
【答案】：
(1)$(x + 2)(x + 4)$
(2)$\pm 6$，$\pm 9$
(3)$(x - 5)(x + 1)(x - 1)(x - 3)$