《2025年作业本江西教育出版社八年级数学上册人教版》

1. 如图所示,在△ABC中,∠1= ∠2,G为AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD于点H.下列判断正确的有③④(填序号).

答案： 【解析】：本题主要考查了三角形的角平分线、中线和高线的定义。
① 对于“$AD$是$\bigtriangleup ABE$的角平分线”：
角平分线的定义是从一个角的顶点出发，将该角平分为两个相等的小角。
但在此题中，$AD$只是$\angle BAC$的角平分线，并不直接说明它是$\bigtriangleup ABE$的角平分线，因为$\bigtriangleup ABE$并不是由$AD$直接分割的。所以①错误。
② 对于“$BE$是$\bigtriangleup ABD$的边$AD$上的中线”：
中线的定义是连接三角形任意两边中点的线段。
但在此题中，$G$是$AD$的中点，而$BE$并没有连接$AB$或$BD$的中点，所以$BE$不是$\bigtriangleup ABD$的边$AD$上的中线。所以②错误。
③ 对于“$CH$是$\bigtriangleup ACD$的边$AD$上的高”：
高的定义是从三角形的一个顶点出发，垂直于对边或对边的延长线。
在此题中，$CF\perp AD$于点$H$，说明$CH$（作为$CF$的一部分）是垂直于$AD$的，因此$CH$是$\bigtriangleup ACD$的边$AD$上的高。所以③正确。
④ 对于“$AH$是$\bigtriangleup ACF$的角平分线和高”：
由于$∠1=∠2$，且$AH$从$A$出发将$\angle CAF$平分为两个相等的小角，所以$AH$是$\bigtriangleup ACF$的角平分线。
同时，由于$CF\perp AD$，所以$AH$（作为$AD$的一部分）也是$\bigtriangleup ACF$的高。所以④正确。
【答案】：③④

2. 如图所示,在△ABC中,AF是中线,AD是角平分线,AE是高.请完成以下填空：
(1)BF= FC= 1/2BC；
(2)∠BAD= ∠DAC= 1/2∠BAC；
(3)∠AEB= ∠AEC= 90°；
(4)S△ABC= $\frac{1}{2}BC\cdot AE$.

答案： 【解析】：
本题主要考查了三角形的中线、角平分线、高的定义及三角形的面积公式。
(1)根据三角形中线的定义：三角形的中线是连接三角形一个顶点和它所对边的中点的线段。
已知$AF$是$\bigtriangleup ABC$的中线，所以$F$为$BC$中点，那么$BF = FC=\frac{1}{2}BC$。
(2)根据三角形角平分线的定义：三角形的一个内角的平分线与它的对边相交，连接这个角的顶点与交点之间的线段叫三角形的角平分线。
已知$AD$是$\bigtriangleup ABC$的角平分线，所以$∠BAD = ∠DAC=\frac{1}{2}∠BAC$。
(3)根据三角形高的定义：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形的高。
已知$AE$是$\bigtriangleup ABC$的高，所以$AE\perp BC$，那么$∠AEB = ∠AEC = 90^{\circ}$。
(4)根据三角形的面积公式：三角形的面积等于底乘以高的一半。
在$\bigtriangleup ABC$中，$BC$为底，$AE$为高，所以$S_{\bigtriangleup ABC}=\frac{1}{2}BC\cdot AE$。
【答案】：
(1)$FC$；$BC$；
(2)$∠DAC$；$∠BAC$；
(3)$∠AEC$；
(4)$\frac{1}{2}BC\cdot AE$。

3. 如图所示.

(1)在△ABC中,BC边上的高是AB；
(2)在△AEC中,AE边上的高是CD.

答案：
(1)$AB$
(2)$CD$

4. 如图所示,AD,AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于点O.若∠ABC= 40°,∠C= 60°,求∠DAE,∠BOE的大小.

答案： 解：在△ABC中，∠ABC=40°，∠C=60°，
∠BAC=180°-∠ABC-∠C=80°.
AE是∠BAC的平分线，
∠BAE=∠CAE=∠BAC/2=40°.
AD是△ABC的高，
∠ADC=90°，
在△ADC中，∠CAD=180°-∠ADC-∠C=30°，
∠DAE=∠CAE-∠CAD=40°-30°=10°.
BF是∠ABC的平分线，
∠ABF=∠ABC/2=20°.
在△ABO中，∠AOB=180°-∠BAE-∠ABF=180°-40°-20°=120°，
∠BOE=180°-∠AOB=60°.
答：∠DAE=10°，∠BOE=60°.

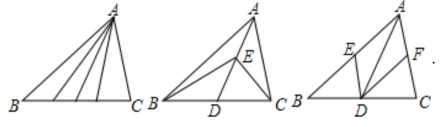
5. 请你通过画图把一个三角形分成面积相等的4个小三角形,要求至少给出3种不同的方案.

答案：