《2025年作业本江西教育出版社八年级数学上册人教版》

20. 如图所示,$ AB = AC $,$ \angle ABD = \angle ACD $.求证$ AD \perp BC $.

答案： 证明：
∵AB=AC，
∴∠ABC=∠ACB（等边对等角）。
∵∠ABD=∠ACD，
∴∠ABC-∠ABD=∠ACB-∠ACD，即∠DBC=∠DCB。
∴DB=DC（等角对等边）。
在△ABD和△ACD中，
∵AB=AC，AD=AD，DB=DC，
∴△ABD≌△ACD（SSS）。
∴∠BAD=∠CAD（全等三角形对应角相等）。
∵AB=AC，
∴AD⊥BC（等腰三角形顶角的平分线垂直于底边）。

21. 如图所示,在$ \triangle ABC $中,$ AB = AC $,$ D 是 BA $延长线上一点,$ E 是 AC $的中点.
(1)实践与操作：利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作$ \angle DAC 的平分线 AM $；
②连接$ BE 并延长交 AM 于点 F $.
(2)猜想与证明：$ AF 与 BC $有怎样的位置关系和数量关系？请证明.

答案：

(1)如图所示

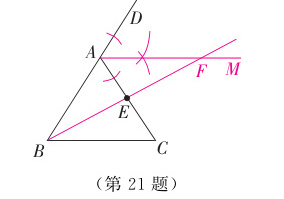
(2)$AF // BC$；$AF = BC$；
证明：
∵$AB = AC$，
∴$\angle ABC = \angle ACB$，
∵$AM$是$\angle DAC$的平分线，
∴$\angle DAF = \angle MAC$，
∵$\angle DAC$是$\triangle ABC$的外角，
∴$\angle DAC = \angle ABC + \angle ACB = 2\angle ABC$，
∵$AM$平分$\angle DAC$，
∴$\angle DAF = \frac{1}{2}\angle DAC = \frac{1}{2} × 2\angle ABC = \angle ABC$，
∴$AF // BC$（内错角相等，两直线平行），
∵$E$是$AC$的中点，
∴$AE = EC$，
∵$\angle AEF = \angle CEB$（对顶角相等），
∴$\triangle AEF \cong \triangle CEB$（AAS），
∴$AF = BC$。

22. 如图所示,在长方形$ ABCD $中,已知$ AB = 6\ cm $,$ BC = 10\ cm $,点$ P 以 4\ cm/s 的速度由点 B 向点 C $运动,同时点$ Q 以 a\ cm/s 的速度由点 C 向点 D $运动.若以$ A,B,P 为顶点的三角形和以 P,C,Q $为顶点的三角形全等,试求$ a $的值.

答案： 解：设运动时间为$ t $秒。
由题意得：$ BP = 4t $，$ PC = BC - BP = 10 - 4t $，$ CQ = at $。
在长方形$ ABCD $中，$ \angle B = \angle C = 90^\circ $。
情况一：$\triangle ABP \cong \triangle PCQ$
则$ AB = PC $，$ BP = CQ $
$ 6 = 10 - 4t $，解得$ t = 1 $
$ 4t = at $，即$ 4 × 1 = a × 1 $，解得$ a = 4 $
情况二：$\triangle ABP \cong \triangle QCP$
则$ AB = QC $，$ BP = PC $
$ 4t = 10 - 4t $，解得$ t = \frac{5}{4} $
$ 6 = a × \frac{5}{4} $，解得$ a = \frac{24}{5} $
综上，$ a $的值为$ 4 $或$ \frac{24}{5} $。