第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 在△ABC中,给定下面几组条件:
①BC= 4 cm,AC= 5 cm,∠ACB= 30°;
②BC= 4 cm,AC= 3 cm,∠ABC= 30°;
③BC= 4 cm,AC= 5 cm,∠ABC= 90°;
④BC= 4 cm,AC= 5 cm,∠ABC= 120°.
若根据每组条件画图,则△ABC能够唯一确定的是______(填序号).
①BC= 4 cm,AC= 5 cm,∠ACB= 30°;
②BC= 4 cm,AC= 3 cm,∠ABC= 30°;
③BC= 4 cm,AC= 5 cm,∠ABC= 90°;
④BC= 4 cm,AC= 5 cm,∠ABC= 120°.
若根据每组条件画图,则△ABC能够唯一确定的是______(填序号).
①③④
答案:
解:①
在△ABC中,BC=4cm,AC=5cm,∠ACB=30°,根据“SAS”可唯一确定三角形。
②
BC=4cm,AC=3cm,∠ABC=30°,由“SSA”可能出现两解,不能唯一确定。
③
BC=4cm,AC=5cm,∠ABC=90°,根据“HL”可唯一确定直角三角形。
④
BC=4cm,AC=5cm,∠ABC=120°,钝角所对边为最长边,AC=5cm>BC=4cm,可唯一确定三角形。
能够唯一确定的是①③④。
答案:①③④
在△ABC中,BC=4cm,AC=5cm,∠ACB=30°,根据“SAS”可唯一确定三角形。
②
BC=4cm,AC=3cm,∠ABC=30°,由“SSA”可能出现两解,不能唯一确定。
③
BC=4cm,AC=5cm,∠ABC=90°,根据“HL”可唯一确定直角三角形。
④
BC=4cm,AC=5cm,∠ABC=120°,钝角所对边为最长边,AC=5cm>BC=4cm,可唯一确定三角形。
能够唯一确定的是①③④。
答案:①③④
2. 如图所示,已知AE= CF,∠AFD= ∠BEC.
(1)若添加条件∠D= ∠B,则AD= BC吗?请说明理由.
(2)若运用“ASA”判定△ADF与△CBE全等,则需添加条件:
(3)若运用“SAS”判定△ADF与△CBE全等,则需添加条件:
(1)若添加条件∠D= ∠B,则AD= BC吗?请说明理由.
(1)AD=BC。理由如下:
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE。
在△ADF和△CBE中,
∠D=∠B,
∠AFD=∠BEC,
AF=CE,
∴△ADF≌△CBE(AAS),
∴AD=BC。
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE。
在△ADF和△CBE中,
∠D=∠B,
∠AFD=∠BEC,
AF=CE,
∴△ADF≌△CBE(AAS),
∴AD=BC。
(2)若运用“ASA”判定△ADF与△CBE全等,则需添加条件:
∠A=∠C
.(3)若运用“SAS”判定△ADF与△CBE全等,则需添加条件:
DF=BE
.
答案:
(1)AD=BC。理由如下:
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE。
在△ADF和△CBE中,
∠D=∠B,
∠AFD=∠BEC,
AF=CE,
∴△ADF≌△CBE(AAS),
∴AD=BC。
(2)∠A=∠C
(3)DF=BE
(1)AD=BC。理由如下:
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE。
在△ADF和△CBE中,
∠D=∠B,
∠AFD=∠BEC,
AF=CE,
∴△ADF≌△CBE(AAS),
∴AD=BC。
(2)∠A=∠C
(3)DF=BE
3. 一个测量工件内槽宽的工具如图所示,O既是AA'的中点,也是BB'的中点.若测得AB= 3.5 cm,求该内槽的宽A'B'.
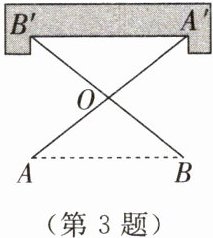

答案:
【解析】:本题可根据全等三角形的判定定理证明$\triangle AOB\cong\triangle A'OB'$,再根据全等三角形的性质求出内槽的宽$A'B'$。
步骤一:分析已知条件
已知$O$既是$AA'$的中点,也是$BB'$的中点,所以可得$AO = A'O$,$BO = B'O$。
又因为$\angle AOB$与$\angle A'OB'$是对顶角,根据对顶角相等的性质,可得$\angle AOB = \angle A'OB'$。
步骤二:证明$\triangle AOB\cong\triangle A'OB'$
在$\triangle AOB$和$\triangle A'OB'$中,
$\begin{cases}AO = A'O\\\angle AOB = \angle A'OB'\\BO = B'O\end{cases}$
根据全等三角形的判定定理“边角边”($SAS$),可以得出$\triangle AOB\cong\triangle A'OB'$。
步骤三:根据全等三角形的性质求出$A'B'$的长度
因为全等三角形的对应边相等,$\triangle AOB\cong\triangle A'OB'$,所以$AB = A'B'$。
已知$AB = 3.5cm$,所以$A'B' = 3.5cm$。
【答案】:$A'B' = 3.5cm$。
步骤一:分析已知条件
已知$O$既是$AA'$的中点,也是$BB'$的中点,所以可得$AO = A'O$,$BO = B'O$。
又因为$\angle AOB$与$\angle A'OB'$是对顶角,根据对顶角相等的性质,可得$\angle AOB = \angle A'OB'$。
步骤二:证明$\triangle AOB\cong\triangle A'OB'$
在$\triangle AOB$和$\triangle A'OB'$中,
$\begin{cases}AO = A'O\\\angle AOB = \angle A'OB'\\BO = B'O\end{cases}$
根据全等三角形的判定定理“边角边”($SAS$),可以得出$\triangle AOB\cong\triangle A'OB'$。
步骤三:根据全等三角形的性质求出$A'B'$的长度
因为全等三角形的对应边相等,$\triangle AOB\cong\triangle A'OB'$,所以$AB = A'B'$。
已知$AB = 3.5cm$,所以$A'B' = 3.5cm$。
【答案】:$A'B' = 3.5cm$。
4. 如图所示,AB= AD,BC= DC,点E在AC上.求证:
(1)AC平分∠BAD;
(2)BE= DE.
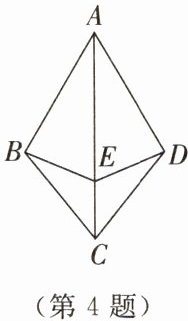
(1)AC平分∠BAD;
(2)BE= DE.

答案:
(1)证明:在△ABC和△ADC中,
∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
即AC平分∠BAD。
(2)证明:由
(1)知∠BAC=∠DAC,
在△BAE和△DAE中,
∵AB=AD,∠BAE=∠DAE,AE=AE,
∴△BAE≌△DAE(SAS),
∴BE=DE。
(1)证明:在△ABC和△ADC中,
∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
即AC平分∠BAD。
(2)证明:由
(1)知∠BAC=∠DAC,
在△BAE和△DAE中,
∵AB=AD,∠BAE=∠DAE,AE=AE,
∴△BAE≌△DAE(SAS),
∴BE=DE。
查看更多完整答案,请扫码查看


