第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
10. 如图所示,$\angle AOB= 30^\circ$,$P是\angle AOB$的平分线上的一点,$PM\perp OB于点M$,$PN// OB交OA于点N$.若$PM= 1$,则$PN= $
2
.
答案:
解:过点P作PH⊥OA于点H。
∵P是∠AOB平分线上一点,PM⊥OB,PH⊥OA,
∴PH=PM=1。
∵PN//OB,∠AOB=30°,
∴∠PNH=∠AOB=30°。
在Rt△PNH中,∠PNH=30°,PH=1,
∴PN=2PH=2×1=2。
答案:2
∵P是∠AOB平分线上一点,PM⊥OB,PH⊥OA,
∴PH=PM=1。
∵PN//OB,∠AOB=30°,
∴∠PNH=∠AOB=30°。
在Rt△PNH中,∠PNH=30°,PH=1,
∴PN=2PH=2×1=2。
答案:2
11. 若等腰三角形的一个角是$80^\circ$,则它的底角是
$80^\circ$或$50^\circ$
.
答案:
【解析】:
本题主要考查等腰三角形的性质。
由等腰三角形的性质,我们知道等腰三角形的两个底角是相等的。
同时,三角形的三个内角之和为$180^\circ$。
当$80^\circ$角为底角时:
设等腰三角形的顶角为$\alpha$,则有两个底角,都为$80^\circ$。
根据三角形内角和为$180^\circ$的性质,有:
$\alpha + 80^\circ + 80^\circ = 180^\circ$,
解得:
$\alpha = 20^\circ$,
此时,底角为$80^\circ$。
当$80^\circ$角为顶角时:
设等腰三角形的两个底角都为$\beta$。
根据三角形内角和为$180^\circ$的性质,有:
$80^\circ + 2\beta = 180^\circ$,
解得:
$\beta = 50^\circ$,
此时,底角为$50^\circ$。
所以,等腰三角形的底角有两种可能:$80^\circ$或$50^\circ$。
【答案】:
$80^\circ$或$50^\circ$。
本题主要考查等腰三角形的性质。
由等腰三角形的性质,我们知道等腰三角形的两个底角是相等的。
同时,三角形的三个内角之和为$180^\circ$。
当$80^\circ$角为底角时:
设等腰三角形的顶角为$\alpha$,则有两个底角,都为$80^\circ$。
根据三角形内角和为$180^\circ$的性质,有:
$\alpha + 80^\circ + 80^\circ = 180^\circ$,
解得:
$\alpha = 20^\circ$,
此时,底角为$80^\circ$。
当$80^\circ$角为顶角时:
设等腰三角形的两个底角都为$\beta$。
根据三角形内角和为$180^\circ$的性质,有:
$80^\circ + 2\beta = 180^\circ$,
解得:
$\beta = 50^\circ$,
此时,底角为$50^\circ$。
所以,等腰三角形的底角有两种可能:$80^\circ$或$50^\circ$。
【答案】:
$80^\circ$或$50^\circ$。
12. 如图所示,$CA\perp AB$,垂足为$A$,$AB= 8\ cm$,$AC= 4\ cm$,射线$BM\perp AB$,垂足为$B$.一动点$E从点A$出发,以$2\ cm/s的速度沿射线AN$运动,$D为射线BM$上一动点,随着点$E$运动而运动,且始终保持$ED= CB$.当点$E$运动______$s$时,点$B,D,E组成的三角形与点A,B,C$组成的三角形全等.
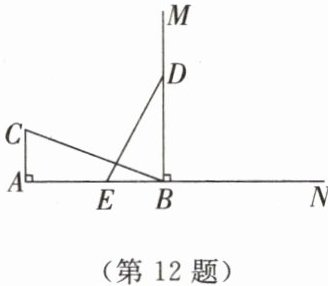

答案:
0,2,6,8
13. 一个三角形的两边$b= 2$,$c= 7$.
(1)当各边均为整数时,可以组成
(2)若此三角形是等腰三角形,则其周长是多少?
(1)当各边均为整数时,可以组成
3
个不同的三角形.(2)若此三角形是等腰三角形,则其周长是多少?
解:当腰长为2时,2+2=4<7,不能构成三角形;
当腰长为7时,7+7>2,能构成三角形,周长为7+7+2=16。
答:其周长是16。
当腰长为7时,7+7>2,能构成三角形,周长为7+7+2=16。
答:其周长是16。
答案:
(1)3
(2)解:当腰长为2时,2+2=4<7,不能构成三角形;
当腰长为7时,7+7>2,能构成三角形,周长为7+7+2=16。
答:其周长是16。
(1)3
(2)解:当腰长为2时,2+2=4<7,不能构成三角形;
当腰长为7时,7+7>2,能构成三角形,周长为7+7+2=16。
答:其周长是16。
14. 如图所示,已知$AB// CD$,$AC平分\angle BAD$.
(1)求证$AD= DC$;
(2)若$\angle D= 120^\circ$,$AC\perp CB$,求$\angle B$的大小.
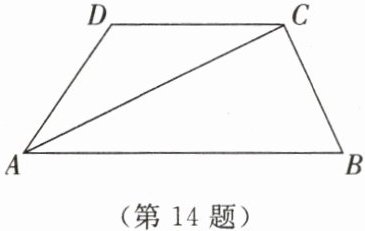
(1)求证$AD= DC$;
(2)若$\angle D= 120^\circ$,$AC\perp CB$,求$\angle B$的大小.

答案:
【解析】:本题主要考查了平行线的性质、角平分线的定义以及等腰三角形的判定和直角三角形的性质。
(1)证明过程需要利用平行线的性质得到内错角相等,再结合角平分线的定义推出两个角相等,最后根据等腰三角形的判定得出结论。
(2)求解过程需要先根据平行线的性质求出$\angle DAB$的度数,再利用角平分线的定义求出$\angle DAC$和$\angle CAB$的度数,最后结合直角三角形的性质求出$\angle B$的度数。
【答案】:
(1)证明:
∵$AB// CD$,
∴$\angle DCA=\angle CAB$(两直线平行,内错角相等)。
∵$AC$平分$\angle BAD$,
∴$\angle DAC=\angle CAB$(角平分线的定义)。
∴$\angle DCA=\angle DAC$。
∴$AD=DC$(等角对等边)。
(2)
∵$AB// CD$,$\angle D = 120^{\circ}$,
∴$\angle DAB=180^{\circ}-\angle D = 180^{\circ}-120^{\circ}=60^{\circ}$(两直线平行,同旁内角互补)。
∵$AC$平分$\angle BAD$,
∴$\angle DAC=\angle CAB=\frac{1}{2}\angle DAB=\frac{1}{2}×60^{\circ}=30^{\circ}$。
∵$AC\perp CB$,
∴$\angle ACB = 90^{\circ}$。
在$\triangle ABC$中,$\angle B=180^{\circ}-\angle CAB-\angle ACB=180^{\circ}-30^{\circ}-90^{\circ}=60^{\circ}$。
∴$\angle B$的大小为$60^{\circ}$。
(1)证明过程需要利用平行线的性质得到内错角相等,再结合角平分线的定义推出两个角相等,最后根据等腰三角形的判定得出结论。
(2)求解过程需要先根据平行线的性质求出$\angle DAB$的度数,再利用角平分线的定义求出$\angle DAC$和$\angle CAB$的度数,最后结合直角三角形的性质求出$\angle B$的度数。
【答案】:
(1)证明:
∵$AB// CD$,
∴$\angle DCA=\angle CAB$(两直线平行,内错角相等)。
∵$AC$平分$\angle BAD$,
∴$\angle DAC=\angle CAB$(角平分线的定义)。
∴$\angle DCA=\angle DAC$。
∴$AD=DC$(等角对等边)。
(2)
∵$AB// CD$,$\angle D = 120^{\circ}$,
∴$\angle DAB=180^{\circ}-\angle D = 180^{\circ}-120^{\circ}=60^{\circ}$(两直线平行,同旁内角互补)。
∵$AC$平分$\angle BAD$,
∴$\angle DAC=\angle CAB=\frac{1}{2}\angle DAB=\frac{1}{2}×60^{\circ}=30^{\circ}$。
∵$AC\perp CB$,
∴$\angle ACB = 90^{\circ}$。
在$\triangle ABC$中,$\angle B=180^{\circ}-\angle CAB-\angle ACB=180^{\circ}-30^{\circ}-90^{\circ}=60^{\circ}$。
∴$\angle B$的大小为$60^{\circ}$。
15. 如图所示,点$A,B,D,E$在同一直线上,$AD= EB$,$AC// EF$,$\angle C= \angle F$.求证$\triangle ABC\cong\triangle EDF$.
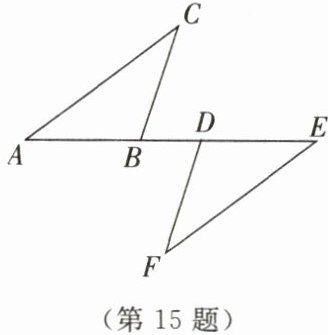

答案:
【解析】:
本题可根据已知条件,通过线段的和差关系得到一组对应边相等,再结合平行线的性质得到一组对应角相等,最后结合已知的另一组对应角相等,利用“角角边”定理来证明两个三角形全等。
已知$AD = EB$,因为$AD=AB + BD$,$EB=BD + DE$,所以$AB + BD=BD + DE$,根据等式的基本性质,两边同时减去$BD$,可得$AB = DE$。
因为$AC// EF$,根据“两直线平行,同位角相等”,所以$\angle A=\angle E$。
在$\triangle ABC$和$\triangle EDF$中,$\angle C = \angle F$,$\angle A=\angle E$,$AB = DE$,满足全等三角形判定定理中的“角角边”($AAS$)。
【答案】:
证明:
∵$AD = EB$,$AD=AB + BD$,$EB=BD + DE$,
∴$AB + BD=BD + DE$,
∴$AB = DE$。
∵$AC// EF$,
∴$\angle A=\angle E$(两直线平行,同位角相等)。
在$\triangle ABC$和$\triangle EDF$中,
$\begin{cases}\angle C = \angle F\\\angle A=\angle E\\AB = DE\end{cases}$
∴$\triangle ABC\cong\triangle EDF(AAS)$。
本题可根据已知条件,通过线段的和差关系得到一组对应边相等,再结合平行线的性质得到一组对应角相等,最后结合已知的另一组对应角相等,利用“角角边”定理来证明两个三角形全等。
已知$AD = EB$,因为$AD=AB + BD$,$EB=BD + DE$,所以$AB + BD=BD + DE$,根据等式的基本性质,两边同时减去$BD$,可得$AB = DE$。
因为$AC// EF$,根据“两直线平行,同位角相等”,所以$\angle A=\angle E$。
在$\triangle ABC$和$\triangle EDF$中,$\angle C = \angle F$,$\angle A=\angle E$,$AB = DE$,满足全等三角形判定定理中的“角角边”($AAS$)。
【答案】:
证明:
∵$AD = EB$,$AD=AB + BD$,$EB=BD + DE$,
∴$AB + BD=BD + DE$,
∴$AB = DE$。
∵$AC// EF$,
∴$\angle A=\angle E$(两直线平行,同位角相等)。
在$\triangle ABC$和$\triangle EDF$中,
$\begin{cases}\angle C = \angle F\\\angle A=\angle E\\AB = DE\end{cases}$
∴$\triangle ABC\cong\triangle EDF(AAS)$。
查看更多完整答案,请扫码查看


