《2025年作业本江西教育出版社八年级数学上册人教版》

8. 如图所示,在$\triangle ABC$中,$\angle A= 40^{\circ}$,$\angle B= 72^{\circ}$,$CE平分\angle ACB$,$CD \perp AB于点D$,$DF \perp CE于点F$.
(1)求$\angle CDF$大小；
(2)若$CD= 12$,$DE= 5$,$CE= 13$,求$DF$的长.

答案：
(1)解：在△ABC中，∠A=40°，∠B=72°，
∠ACB=180°-∠A-∠B=180°-40°-72°=68°.
∵CE平分∠ACB，
∴∠ACE=∠BCE=∠ACB/2=34°.
∵CD⊥AB，
∴∠CDB=90°，∠BCD=90°-∠B=90°-72°=18°.
∠DCE=∠BCE-∠BCD=34°-18°=16°.
∵DF⊥CE，
∴∠DFC=90°，∠CDF=90°-∠DCE=90°-16°=74°.
(2)解：S△CDE=CD·DE/2=12×5/2=30.
又S△CDE=CE·DF/2=13·DF/2，
13·DF/2=30，DF=60/13.

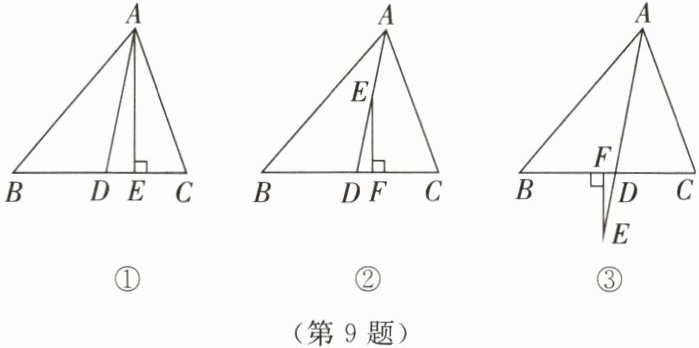
9. 在$\triangle ABC$中,$AD平分\angle BAC$,$\angle B＜\angle C$.
(1)如图①所示,$AE$是高,$\angle B= 50^{\circ}$,$\angle C= 70^{\circ}$,求$\angle DAE$的大小；
(2)如图②所示,点$E在AD$上,$EF \perp BC于点F$,试探究$\angle DEF与\angle B$,$\angle C$的大小关系,并证明你的结论；
(3)如图③所示,点$E在AD$的延长线上,$EF \perp BC于点F$,则$\angle DEF与\angle B$,$\angle C$之间的数量关系是______(直接写出结论).

【答案】：
（1）$\angle DAE = 10^\circ$；
（2）$\angle DEF = \frac{1}{2} (\angle C - \angle B)$，证明见上述详解；
（3）$\angle DEF = \frac{1}{2} (\angle C - \angle B)$。

答案： 【解析】：本题主要考查了三角形内角和定理、角平分线的性质以及直角三角形的性质。
（1）首先，根据三角形内角和为$180^\circ$，求出$\angle BAC$的度数：
$\angle BAC = 180^\circ - \angle B - \angle C = 180^\circ - 50^\circ - 70^\circ = 60^\circ$，
由于$AD$平分$\angle BAC$，根据角平分线的性质，有：
$\angle BAD = \frac{1}{2} \angle BAC = \frac{1}{2} × 60^\circ = 30^\circ$，
在直角三角形$ABE$中，$\angle BAE = 90^\circ - \angle B = 90^\circ - 50^\circ = 40^\circ$，
因此，$\angle DAE = \angle BAE - \angle BAD = 40^\circ - 30^\circ = 10^\circ$。
（2）过点$A$作$AG \perp BC$于点$G$。
根据三角形内角和定理，有：
$\angle BAG = 90^\circ - \angle B$，
$\angle CAG = 90^\circ - \angle C$，
由于$AD$平分$\angle BAC$，根据角平分线的性质，有：
$\angle BAD = \angle CAD$，
因此，$\angle DAE = \angle BAG - \angle BAD = \angle BAG - \angle CAD = (90^\circ - \angle B) - \frac{1}{2} \angle BAC = (90^\circ - \angle B) - \frac{1}{2} (180^\circ - \angle B - \angle C) = \frac{1}{2} (\angle C - \angle B)$，
又因为$EF \perp BC$，
所以$AG// EF$，
根据平行线的性质，有：
$\angle DEF = \angle DAE = \frac{1}{2} (\angle C - \angle B)$。
（3）类似（2）可得，$\angle DEF = \frac{1}{2}(\angle C - \angle B)$。
【答案】：
（1）$\angle DAE = 10^\circ$；
（2）$\angle DEF = \frac{1}{2} (\angle C - \angle B)$，证明见上述详解；
（3）$\angle DEF = \frac{1}{2} (\angle C - \angle B)$。